|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Координаты вектора</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Координаты вектора, вектор, Координаты, параллельным переносом</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Координаты вектора''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Координаты вектора''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' КООРДИНАТЫ ВЕКТОРА''' | + | '''Координаты вектора''' |
| | | | |
| - | <br>Пусть вектор [[Image:23-06-1.jpg]] имеет началом точку А<sub>1</sub> (х<sub>1</sub>; у<sub>1</sub>), а концом — точку А<sub>2</sub> (x<sub>2</sub>; y<sub>2</sub>). Координатами вектора [[Image:23-06-1.jpg]] будем называть числа а<sub>1</sub>=x<sub>2</sub> — х<sub>1</sub>, a<sub>2</sub> = y<sub>2</sub> — y<sub>1</sub>. Координаты вектора будем ставить рядом с буквенным обозначением вектора, в данном случае<br>[[Image:23-06-1.jpg]](а<sub>1</sub>;а<sub>2</sub>) или просто [[Image:23-06-10.jpg]]. Координаты нулевого вектора равны нулю.<br>Из формулы, выражающей расстояние между двумя точками через их координаты, следует, что абсолютная величина вектора с координатами a<sub>1</sub>, a<sub>2</sub> равна [[Image:23-06-11.jpg]].<br>'''''Равные векторы имеют равные соответствующие координаты. И обратно: если у векторов соответствующие координаты равны, то векторы равны.''''' | + | <br>Пусть [[Презентація уроку: Означення вектора. Модуль і напрям вектора.Рівні вектори|вектор]] [[Image:23-06-1.jpg]] имеет началом точку А<sub>1</sub> (х<sub>1</sub>; у<sub>1</sub>), а концом — точку А<sub>2</sub> (x<sub>2</sub>; y<sub>2</sub>). Координатами вектора [[Image:23-06-1.jpg]] будем называть числа а<sub>1</sub>=x<sub>2</sub> — х<sub>1</sub>, a<sub>2</sub> = y<sub>2</sub> — y<sub>1</sub>. Координаты вектора будем ставить рядом с буквенным обозначением вектора, в данном случае [[Image:23-06-1.jpg]](а<sub>1</sub>;а<sub>2</sub>) или просто [[Image:23-06-10.jpg|Координаты вектора]]. [[Координаты середины отрезка|Координаты]] нулевого вектора равны нулю.<br> |
| | | | |
| - | Действительно, пусть А<sub>1</sub> (х<sub>1</sub>; у<sub>1</sub>) и А<sub>2</sub> (х<sub>2</sub>; у<sub>2</sub>) — начало и конец вектора [[Image:23-06-1.jpg]]. Так как равный ему вектор [[Image:23-06-1.jpg]]' получается из вектора [[Image:23-06-1.jpg]] параллельным переносом, то его началом и концом будут соответственно A<sub>1</sub>'(х<sub>1</sub> + с; y<sub>1</sub>+d), А'<sub>2</sub>-(x<sub>2</sub> + с; y<sub>2</sub> + d). Отсюда видно, что оба вектора [[Image:23-06-1.jpg]] и [[Image:23-06-1.jpg]]' имеют одни и те же координаты: x<sub>2</sub> — х<sub>1</sub>, у<sub>2</sub> — у<sub>1</sub>.
| + | Из формулы, выражающей расстояние между двумя точками через их координаты, следует, что абсолютная величина вектора с координатами a<sub>1</sub>, a<sub>2</sub> равна [[Image:23-06-11.jpg|Координаты вектора]].<br> |
| | | | |
| - | Докажем теперь обратное утверждение. Пусть соответствующие координаты векторов [[Image:23-06-12.jpg]] равны. Докажем, что векторы равны.<br>Пусть x'<sub>1</sub> и. у'<sub>1</sub> — координаты точки А'<sub>1</sub>, а х'<sub>2</sub>, y'<sub>2</sub> — координаты точки А'<sub>2 </sub> По условию теоремы x<sub>2</sub> — x<sub>1</sub>=x'<sub>2</sub> — x'<sub>1</sub>, y<sub>2</sub> — y<sub>1</sub> = y'<sub>2</sub> — y'<sub>1</sub>.
| + | Равные векторы имеют равные соответствующие координаты. И обратно: если у векторов соответствующие координаты равны, то векторы равны. |
| | | | |
| - | Отсюда x'<sub>2</sub> = x<sub>2</sub> + x'<sub>1 - </sub>х<sub>1</sub>, y'<sub>2</sub> = y<sub>2</sub> + y'<sub>1 - </sub>y<sub>1</sub>,. Параллельный перенос, заданный формулами
| + | Действительно, пусть А<sub>1</sub> (х<sub>1</sub>; у<sub>1</sub>) и А<sub>2</sub> (х<sub>2</sub>; у<sub>2</sub>) — начало и конец вектора [[Image:23-06-1.jpg]]. Так как равный ему вектор [[Image:23-06-1.jpg]]' получается из вектора [[Image:23-06-1.jpg]] [[Презентація уроку: Поворот. Паралельне перенесення|параллельным переносом]], то его началом и концом будут соответственно A<sub>1</sub>'(х<sub>1</sub> + с; y<sub>1</sub>+d), А'<sub>2</sub>-(x<sub>2</sub> + с; y<sub>2</sub> + d). Отсюда видно, что оба вектора [[Image:23-06-1.jpg]] и [[Image:23-06-1.jpg]]' имеют одни и те же координаты: x<sub>2</sub> — х<sub>1</sub>, у<sub>2</sub> — у<sub>1</sub>. |
| | | | |
| - | x' = x+x'<sub>1</sub>—x<sub>1</sub>, y' = y+y'<sub>1</sub>—y<sub>1</sub>,
| + | Докажем теперь обратное утверждение. Пусть соответствующие координаты векторов [[Image:23-06-12.jpg|Координаты вектора]] равны. Докажем, что векторы равны.<br> |
| | | | |
| - | переводит точку А<sub>1</sub> в точку А'<sub>1</sub>, а точку А<sub>2</sub> в точку А'<sub>2</sub>, т. е. векторы [[Image:23-06-12.jpg]] равны, что и требовалось доказать.
| + | Пусть x'<sub>1</sub> и. у'<sub>1</sub> — координаты точки А'<sub>1</sub>, а х'<sub>2</sub>, y'<sub>2</sub> — координаты точки А'<sub>2 </sub> По условию теоремы x<sub>2</sub> — x<sub>1</sub>=x'<sub>2</sub> — x'<sub>1</sub>, y<sub>2</sub> — y<sub>1</sub> = y'<sub>2</sub> — y'<sub>1</sub>. |
| | | | |
| - | Задача (7). Даны три точки А (1; 1), В ( —1;0), С (0; 1). Найдите такую точку D(х; у), чтобы векторы [[Image:23-06-3.jpg]] и [[Image:23-06-5.jpg]] были равны. | + | Отсюда x'<sub>2</sub> = x<sub>2</sub> + x'<sub>1 - </sub>х<sub>1</sub>, y'<sub>2</sub> = y<sub>2</sub> + y'<sub>1 - </sub>y<sub>1</sub>,. Параллельный перенос, заданный формулами x' = x+x'<sub>1</sub>—x<sub>1</sub>, y' = = y+y'<sub>1</sub>—y<sub>1</sub>, переводит точку А<sub>1</sub> в точку А'<sub>1</sub>, а точку А<sub>2</sub> в точку А'<sub>2</sub>, т. е. векторы [[Image:23-06-12.jpg|Координаты вектора]] равны, что и требовалось доказать. |
| | + | |
| | + | '''Задача (7)'''. Даны три точки А (1; 1), В ( —1;0), С (0; 1). Найдите такую точку D(х; у), чтобы векторы [[Image:23-06-3.jpg]] и [[Image:23-06-5.jpg]] были равны. |
| | + | |
| | + | '''Решение'''. Вектор [[Image:23-06-3.jpg]] имеет координаты —2, —1. Вектор [[Image:23-06-5.jpg]] имеет координаты x —0, y — 1. Так как [[Image:23-06-3.jpg]]= [[Image:23-06-5.jpg]], то x—0=—2, y—1=—1. Отсюда находим координаты точки D: х=—2, у — 0. <br> |
| | + | |
| | + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | Решение. Вектор [[Image:23-06-3.jpg]] имеет координаты —2, —1. Вектор [[Image:23-06-5.jpg]] имеет координаты x —0, y — 1. Так как [[Image:23-06-3.jpg]]= [[Image:23-06-5.jpg]], то x—0=—2, y—1=—1. Отсюда находим координаты точки D: х=—2, у — О. <br>
| |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Календарно-тематическое планирование по математике, задачи и ответы школьнику [[Гипермаркет знаний - первый в мире!|онлайн]], курсы учителю по математике [[Математика|скачать]]</sub> | | <sub>Календарно-тематическое планирование по математике, задачи и ответы школьнику [[Гипермаркет знаний - первый в мире!|онлайн]], курсы учителю по математике [[Математика|скачать]]</sub> |
| Строка 30: |
Строка 34: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 15:53, 9 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Координаты вектора
Координаты вектора
Пусть вектор  имеет началом точку А1 (х1; у1), а концом — точку А2 (x2; y2). Координатами вектора имеет началом точку А1 (х1; у1), а концом — точку А2 (x2; y2). Координатами вектора  будем называть числа а1=x2 — х1, a2 = y2 — y1. Координаты вектора будем ставить рядом с буквенным обозначением вектора, в данном случае будем называть числа а1=x2 — х1, a2 = y2 — y1. Координаты вектора будем ставить рядом с буквенным обозначением вектора, в данном случае  (а1;а2) или просто (а1;а2) или просто 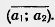 . Координаты нулевого вектора равны нулю. . Координаты нулевого вектора равны нулю.
Из формулы, выражающей расстояние между двумя точками через их координаты, следует, что абсолютная величина вектора с координатами a1, a2 равна 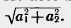 . .
Равные векторы имеют равные соответствующие координаты. И обратно: если у векторов соответствующие координаты равны, то векторы равны.
Действительно, пусть А1 (х1; у1) и А2 (х2; у2) — начало и конец вектора  . Так как равный ему вектор . Так как равный ему вектор  ' получается из вектора ' получается из вектора  параллельным переносом, то его началом и концом будут соответственно A1'(х1 + с; y1+d), А'2-(x2 + с; y2 + d). Отсюда видно, что оба вектора параллельным переносом, то его началом и концом будут соответственно A1'(х1 + с; y1+d), А'2-(x2 + с; y2 + d). Отсюда видно, что оба вектора  и и  ' имеют одни и те же координаты: x2 — х1, у2 — у1. ' имеют одни и те же координаты: x2 — х1, у2 — у1.
Докажем теперь обратное утверждение. Пусть соответствующие координаты векторов  равны. Докажем, что векторы равны. равны. Докажем, что векторы равны.
Пусть x'1 и. у'1 — координаты точки А'1, а х'2, y'2 — координаты точки А'2 По условию теоремы x2 — x1=x'2 — x'1, y2 — y1 = y'2 — y'1.
Отсюда x'2 = x2 + x'1 - х1, y'2 = y2 + y'1 - y1,. Параллельный перенос, заданный формулами x' = x+x'1—x1, y' = = y+y'1—y1, переводит точку А1 в точку А'1, а точку А2 в точку А'2, т. е. векторы  равны, что и требовалось доказать. равны, что и требовалось доказать.
Задача (7). Даны три точки А (1; 1), В ( —1;0), С (0; 1). Найдите такую точку D(х; у), чтобы векторы  и и 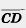 были равны. были равны.
Решение. Вектор  имеет координаты —2, —1. Вектор имеет координаты —2, —1. Вектор 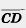 имеет координаты x —0, y — 1. Так как имеет координаты x —0, y — 1. Так как  = = 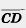 , то x—0=—2, y—1=—1. Отсюда находим координаты точки D: х=—2, у — 0. , то x—0=—2, y—1=—1. Отсюда находим координаты точки D: х=—2, у — 0.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Календарно-тематическое планирование по математике, задачи и ответы школьнику онлайн, курсы учителю по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|










