|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | '''РАЗЛОЖЕНИЕ ВЕКТОРА ПО КООРДИНАТНЫМ ОСЯМ''' | + | '''РАЗЛОЖЕНИЕ ВЕКТОРА ПО КООРДИНАТНЫМ ОСЯМ''' |
| | | | |
| | + | <br> |
| | | | |
| | + | <br> |
| | | | |
| | + | [[Image:23-06-62.jpg]] |
| | | | |
| - | | + | '''''<br>Вектор называется единичным, если его абсолютная величина равна единице.''''' Единичные векторы, имеющие направления положительных координатных полуосей, называются '''''координатными векторами или ортами'''''. Мы будем их обозначать [[Image:23-06-63.jpg]]<sub>1</sub> (1; 0) на оси х и [[Image:23-06-63.jpg]]<sub>2</sub>С0; 1) на оси у (рис. 227).<br>Так как координатные векторы отличны от нуля и не коллинеарны, то любой вектор [[Image:23-06-1.jpg]](a<sub>1</sub>;c<sub>2</sub>) допускает разложение по этим векторам: |
| - | [[Image:23-06-62.jpg]]''
| + | |
| - | | + | |
| - | '''''<br>Вектор называется единичным, если его абсолютная величина равна единице.''''' Единичные векторы, имеющие направления положительных координатных полуосей, называются '''''координатными векторами или ортами'''''. Мы будем их обозначать [[Image:23-06-63.jpg]]<sub>1</sub> (1; 0) на оси х и [[Image:23-06-63.jpg]]<sub>2</sub>С0; 1) на оси у (рис. 227).<br>Так как координатные векторы отличны от нуля и не коллинеарны, то любой вектор [[Image:23-06-1.jpg]](a<sub>1</sub>;c<sub>2</sub>) допускает разложение по этим векторам: | + | |
| | | | |
| | [[Image:23-06-64.jpg]]<br><br>Найдем коэффициенты [[Image:23-06-65.jpg]], этого разложения. Умножим обе части равенства (*) на вектор [[Image:23-06-63.jpg]]<sub>1</sub>. Так как | | [[Image:23-06-64.jpg]]<br><br>Найдем коэффициенты [[Image:23-06-65.jpg]], этого разложения. Умножим обе части равенства (*) на вектор [[Image:23-06-63.jpg]]<sub>1</sub>. Так как |
| | | | |
| - | [[Image:23-06-66.jpg]] | + | [[Image:23-06-66.jpg]] |
| | | | |
| - | Аналогично, умножая обе части равенства (*) на вектор [[Image:23-06-63.jpg]]<sub>2</sub>, получим | + | Аналогично, умножая обе части равенства (*) на вектор [[Image:23-06-63.jpg]]<sub>2</sub>, получим |
| | | | |
| | [[Image:23-06-67.jpg]]<br>Таким образом, для любого вектора [[Image:23-06-1.jpg]](a<sub>1</sub>;c<sub>2</sub>) получается разложение<br>[[Image:23-06-68.jpg]] | | [[Image:23-06-67.jpg]]<br>Таким образом, для любого вектора [[Image:23-06-1.jpg]](a<sub>1</sub>;c<sub>2</sub>) получается разложение<br>[[Image:23-06-68.jpg]] |
| Строка 25: |
Строка 25: |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | <sub>Видео по математике[[Математика|скачать]], домашнее задание, учителям и школьникам на помощь [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | + | <sub>Видео по математике [[Математика|скачать]], домашнее задание, учителям и школьникам на помощь [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
| | | | |
| | <br> | | <br> |
Версия 08:48, 23 июня 2010
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Разложение вектора по координатным осям
РАЗЛОЖЕНИЕ ВЕКТОРА ПО КООРДИНАТНЫМ ОСЯМ
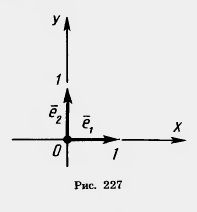
Вектор называется единичным, если его абсолютная величина равна единице. Единичные векторы, имеющие направления положительных координатных полуосей, называются координатными векторами или ортами. Мы будем их обозначать 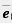 1 (1; 0) на оси х и 1 (1; 0) на оси х и 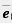 2С0; 1) на оси у (рис. 227). 2С0; 1) на оси у (рис. 227).
Так как координатные векторы отличны от нуля и не коллинеарны, то любой вектор  (a1;c2) допускает разложение по этим векторам: (a1;c2) допускает разложение по этим векторам:

Найдем коэффициенты 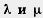 , этого разложения. Умножим обе части равенства (*) на вектор , этого разложения. Умножим обе части равенства (*) на вектор 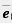 1. Так как 1. Так как
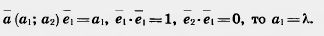
Аналогично, умножая обе части равенства (*) на вектор 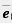 2, получим 2, получим
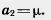
Таким образом, для любого вектора  (a1;c2) получается разложение (a1;c2) получается разложение
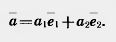
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|











