|
|
|
| Строка 3: |
Строка 3: |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Задачи-2(9-класс)''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Задачи-2(9-класс)''' |
| | | | |
| | + | <br> ''' ЗАДАЧИ''' |
| | | | |
| - | ''' ЗАДАЧИ'''
| + | <br>1. Стороны треугольника 5 м, 6 м, 7 м. Найдите косинусы углов треугольника. |
| | | | |
| - | <br>1. Стороны треугольника 5 м, 6 м, 7 м. Найдите косинусы углов треугольника.
| + | 2. У треугольника две стороны равны 5 м и 6 м, а синус угла между ними равен 0,6. Найдите третью сторону. |
| | | | |
| - | 2. У треугольника две стороны равны 5 м и 6 м, а синус угла между ними равен 0,6. Найдите третью сторону.
| + | 3. Стороны треугольника равны а, b, с. Докажите, что если а<sup>2</sup>+Ь<sup>2</sup>>с<sup>2</sup>, то угол, противолежащий стороне с, острый. Если а<sup>2</sup>+Ь<sup>2</sup>< с<sup>2</sup>, то угол, противолежащий стороне с, тупой. |
| | | | |
| - | 3. Стороны треугольника равны а, b, с. Докажите, что если а<sup>2</sup>+Ь<sup>2</sup>>с<sup>2</sup>, то угол, противолежащий стороне с, острый. Если а<sup>2</sup>+Ь<sup>2</sup>< с<sup>2</sup>, то угол, противолежащий стороне с, тупой.
| + | 4. Даны диагонали параллелограмма с и d и угол между ними а. Найдите стороны параллелограмма. |
| | | | |
| - | 4. Даны диагонали параллелограмма с и d и угол между ними а. Найдите стороны параллелограмма.
| + | 5. Даны стороны параллелограмма а и b тл один из углов [[Image:24-06-52.jpg]]. Найдите диагонали параллелограмма. |
| | | | |
| - | 5. Даны стороны параллелограмма а и b тл один из углов [[Image:24-06-52.jpg]]. Найдите диагонали параллелограмма.
| + | 6. Стороны треугольника 4 м, 5 м и 6 м. Найдите проекции сторон 4 м и 5 м на прямую, содержащую сторону 6 м. |
| | | | |
| - | 6. Стороны треугольника 4 м, 5 м и 6 м. Найдите проекции сторон 4 м и 5 м на прямую, содержащую сторону 6 м.
| + | 7. Даны стороны треугольника а, b, с. Найдите высоту треугольника, опущенную на сторону с. |
| | | | |
| - | 7. Даны стороны треугольника а, b, с. Найдите высоту треугольника, опущенную на сторону с.
| + | 8. Найдите высоты треугольника в задаче 1. |
| | | | |
| - | 8. Найдите высоты треугольника в задаче 1.
| + | 9. Найдите медианы треугольника в задаче 1. |
| | | | |
| - | 9. Найдите медианы треугольника в задаче 1.
| + | 10*. Найдите биссектрисы треугольника в задаче 1. |
| | | | |
| - | 10*. Найдите биссектрисы треугольника в задаче 1.
| + | 11*. Как изменяется сторона АВ треугольника ABC, если угол С возрастает, а длины сторон АС и ВС остаются без изменений (рис. 270)? |
| | | | |
| - | 11*. Как изменяется сторона АВ треугольника ABC, если угол С возрастает, а длины сторон АС и ВС остаются без изменений (рис. 270)?
| + | 12. У треугольника ABC АВ—15 см, АС =10 см. Может ли [[Image:24-06-68.jpg]]? |
| | | | |
| - | I 12. У треугольника ABC АВ—15 см, АС =10 см. Может ли [[Image:24-06-68.jpg]]?
| + | 13. Докажите, что в теореме синусов каждое из трех отношений [[Image:24-06-69.jpg]] равно 2R, где R — радиус окружности, описанной около треугольника. |
| | | | |
| - | 13. Докажите, что в теореме синусов каждое из трех отношений [[Image:24-06-69.jpg]] равно 2R, где R — радиус окружности, описанной около треугольника.
| + | 14. Как найти радиус окружности, описанной около треугольника, зная его стороны? Найдите радиус окружности, описанной около треугольника со сторонами 5 м, 6 м, 7 м. |
| | | | |
| - | 14. Как найти радиус окружности, описанной около треугольника, зная его стороны? Найдите радиус окружности, описанной около треугольника со сторонами 5 м, 6 м, 7 м.
| + | 15. Объясните, как найти расстояние от точки А до недоступной точки В (рис. 271), зная расстояние АС и углы [[Image:24-06-52.jpg]] и [[Image:24-06-53.jpg]]. |
| | | | |
| - | 15. Объясните, как найти расстояние от точки А до недоступной точки В (рис. 271), зная расстояние АС и углы а. и [3.<br><br>16. Объясните, как найти высоту х здания (рис. 272) по углам<br> а и Р и расстоянию а.<br>17. Докажите, что если в треугольнике есть тупой угол, то противолежащая ему сторона наибольшая.<br>18. В треугольнике ABC Z.A = 40°, ZB = 60°, ZC = 80°. Какая из сторон треугольника наибольшая, какая — наименьшая?<br>19. У треугольника ABC стороны AS = 5,1 м, ВС = 6,2 м, АС =7,3 м. Какой из углов треугольника наибольший, какой — наименьший?<br> <br> <br>20. Что больше — основание или боковая сторона равнобедренного треугольника, если прилежаш;ий к основанию угол больше 60°?<br>21. У треугольника ABC угол С тупой. Докажите, что если точка X лежит на стороне АС, то ВХ<САВ.<br>22. У треугольника ABC угол С тупой. Докажите, что если точка X лежит на стороне АС, а точка Y — на стороне ВС,<br>то ХУ<:АВ.<br>23. На стороне АВ треугольника ABC отмечена точка D.<br>Докажите, что отрезок CD меньше по крайней мере одной<br>из сторон: АС или ВС.<br>24*. Дан треугольник ABC. CD — медиана, проведенная к стороне АВ. Докажите, что если АС>ВС, то угол ACD меньше угла BCD.<br>25*. Докажите, что биссектриса треугольника не меньше высоты и не больше медианы, проведенных из этой же вершины.<br>26. Даны сторона и два угла треугольника. Найдите третий угол и остальные две стороны, если:<br>112<br><br>1) а = 5. (3 = 30°, Y = 45°;<br>2) а = 20, a = 75V (3 = 60°;<br>3) о = 35, (3 = 40°, Y = 120°;<br>4) Ь = 12, а = 36°, [3 = 25°;<br>5) с = 14. а = 64°. [3 = 48°.<br>27. Даны две стороны и угол между ними. Найдите остальные два угла и третью сторону, если:<br><br>1) о = 12, Ь = 8, V = 60°;<br>2) а = 7. Ь = 23, Y=130°;<br>3) Ь = 9, с=17. а = 95°;<br>4) Ь = 14, с =10, а =145°;<br>5) а = 32. с = 23, (3 = 152°;<br>6) о = 24, с = 18, [3=15°.<br>28. В треугольнике заданы две стороны и угол, противолежащий одной из сторон. Найдите остальные углы и сторону треугольника, если:<br><br>1) а = 12. Ь = 5, а = 120°<br>2) а = 27, Ь = 9, а = 138°;<br>3) о = 34, Ь = 12, а = 164°;<br>4) а = 2. Ь = 4, а = 60°;<br>5) а = 6. Ь = 8, ос = 30°.<br>29. Даны три стороны треугольника. Найдите его углы, если:<br><br>1) а = 2. ь=г. с = 4;<br>2) а = 7. Ь = 2, с = 8;<br>3) а = 4. Ь = 5, с = 7;<br>4) о = 15, Ь = 24, с = 18;<br>5) о = 23, Ь = 17, с = 39;<br>6) а = 55, Ь = 21, с = 38.<br><br><br>
| + | 16. Объясните, как найти высоту х здания (рис. 272) по углам [[Image:24-06-52.jpg]] и [[Image:24-06-53.jpg]] и расстоянию а. |
| | + | |
| | + | 17. Докажите, что если в треугольнике есть тупой угол, то противолежащая ему сторона наибольшая. |
| | + | |
| | + | 18. В треугольнике ABC [[Image:20-06-61.jpg]]A = 40°, [[Image:20-06-61.jpg]]B = 60°, [[Image:20-06-61.jpg]]C = 80°. Какая из сторон треугольника наибольшая, какая — наименьшая? |
| | + | |
| | + | 19. У треугольника ABC стороны AS = 5,1 м, ВС = 6,2 м, АС =7,3 м. Какой из углов треугольника наибольший, какой — наименьший? |
| | + | |
| | + | [[Image:24-06-70.jpg]] |
| | + | |
| | + | 20. Что больше — основание или боковая сторона равнобедренного треугольника, если прилежащий к основанию угол больше 60°? |
| | + | |
| | + | 21. У треугольника ABC угол С тупой. Докажите, что если точка X лежит на стороне АС, то ВХ<АВ. |
| | + | |
| | + | 22. У треугольника ABC угол С тупой. Докажите, что если точка X лежит на стороне АС, а точка Y — на стороне ВС,<br>то ХУ<АВ. |
| | + | |
| | + | 23. На стороне АВ треугольника ABC отмечена точка D.Докажите, что отрезок CD меньше по крайней мере одной из сторон: АС или ВС. |
| | + | |
| | + | 24*. Дан треугольник ABC. CD — медиана, проведенная к стороне АВ. Докажите, что если АС>ВС, то угол ACD меньше угла BCD. |
| | + | |
| | + | 25*. Докажите, что биссектриса треугольника не меньше высоты и не больше медианы, проведенных из этой же вершины. |
| | + | |
| | + | 26. Даны сторона и два угла треугольника. Найдите третий угол и остальные две стороны, если:<br><br>1) а = 5. [[Image:24-06-53.jpg]] = 30°, [[Image:24-06-56.jpg]] = 45°;<br>2) а = 20, [[Image:24-06-52.jpg]] = 75° [[Image:24-06-53.jpg]]= 60°;<br>3) a = 35, [[Image:24-06-53.jpg]] = 40°, [[Image:24-06-56.jpg]] = 120°;<br>4) b = 12, [[Image:24-06-52.jpg]]= 36°, [[Image:24-06-53.jpg]] = 25°;<br>5) с = 14. [[Image:24-06-52.jpg]] = 64°. [[Image:24-06-53.jpg]] = 48°. |
| | + | |
| | + | 27. Даны две стороны и угол между ними. Найдите остальные два угла и третью сторону, если:<br><br>1) a = 12, b = 8, [[Image:24-06-56.jpg]] = 60°;<br>2) а = 7. b = 23, [[Image:24-06-56.jpg]]=130°;<br>3) b = 9, с=17. [[Image:24-06-52.jpg]] = 95°;<br>4) b = 14, с =10, [[Image:24-06-52.jpg]] =145°;<br>5) а = 32. с = 23, [[Image:24-06-53.jpg]] = 152°;<br>6) a = 24, с = 18, [[Image:24-06-53.jpg]]=15°. |
| | + | |
| | + | <br>28. В треугольнике заданы две стороны и угол, противолежащий одной из сторон. Найдите остальные углы и сторону треугольника, если:<br><br>1) а = 12. b = 5, [[Image:24-06-52.jpg]] = 120°<br>2) а = 27, Ь = 9, [[Image:24-06-52.jpg]] = 138°;<br>3) a = 34, Ь = 12, [[Image:24-06-52.jpg]] = 164°;<br>4) а = 2. b = 4, [[Image:24-06-52.jpg]] = 60°;<br>5) а = 6. b = 8, [[Image:24-06-52.jpg]] = 30°. |
| | + | |
| | + | <br>29. Даны три стороны треугольника. Найдите его углы, если:<br><br>1) а = 2. b=г. с = 4;<br>2) а = 7. b = 2, с = 8;<br>3) а = 4. b = 5, с = 7;<br>4) a = 15, b = 24, с = 18;<br>5) a = 23, b = 17, с = 39;<br>6) а = 55, b = 21, с = 38.<br><br><br> |
| | | | |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
Версия 11:44, 24 июня 2010
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика:Задачи-2(9-класс)
ЗАДАЧИ
1. Стороны треугольника 5 м, 6 м, 7 м. Найдите косинусы углов треугольника.
2. У треугольника две стороны равны 5 м и 6 м, а синус угла между ними равен 0,6. Найдите третью сторону.
3. Стороны треугольника равны а, b, с. Докажите, что если а2+Ь2>с2, то угол, противолежащий стороне с, острый. Если а2+Ь2< с2, то угол, противолежащий стороне с, тупой.
4. Даны диагонали параллелограмма с и d и угол между ними а. Найдите стороны параллелограмма.
5. Даны стороны параллелограмма а и b тл один из углов  . Найдите диагонали параллелограмма. . Найдите диагонали параллелограмма.
6. Стороны треугольника 4 м, 5 м и 6 м. Найдите проекции сторон 4 м и 5 м на прямую, содержащую сторону 6 м.
7. Даны стороны треугольника а, b, с. Найдите высоту треугольника, опущенную на сторону с.
8. Найдите высоты треугольника в задаче 1.
9. Найдите медианы треугольника в задаче 1.
10*. Найдите биссектрисы треугольника в задаче 1.
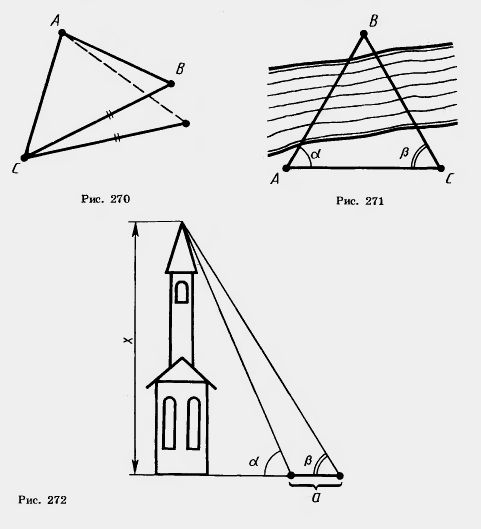
11*. Как изменяется сторона АВ треугольника ABC, если угол С возрастает, а длины сторон АС и ВС остаются без изменений (рис. 270)?
12. У треугольника ABC АВ—15 см, АС =10 см. Может ли 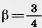 ? ?
13. Докажите, что в теореме синусов каждое из трех отношений 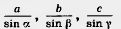 равно 2R, где R — радиус окружности, описанной около треугольника. равно 2R, где R — радиус окружности, описанной около треугольника.
14. Как найти радиус окружности, описанной около треугольника, зная его стороны? Найдите радиус окружности, описанной около треугольника со сторонами 5 м, 6 м, 7 м.
15. Объясните, как найти расстояние от точки А до недоступной точки В (рис. 271), зная расстояние АС и углы  и и  . .
16. Объясните, как найти высоту х здания (рис. 272) по углам  и и  и расстоянию а. и расстоянию а.
17. Докажите, что если в треугольнике есть тупой угол, то противолежащая ему сторона наибольшая.
18. В треугольнике ABC  A = 40°, A = 40°,  B = 60°, B = 60°,  C = 80°. Какая из сторон треугольника наибольшая, какая — наименьшая? C = 80°. Какая из сторон треугольника наибольшая, какая — наименьшая?
19. У треугольника ABC стороны AS = 5,1 м, ВС = 6,2 м, АС =7,3 м. Какой из углов треугольника наибольший, какой — наименьший?
20. Что больше — основание или боковая сторона равнобедренного треугольника, если прилежащий к основанию угол больше 60°?
21. У треугольника ABC угол С тупой. Докажите, что если точка X лежит на стороне АС, то ВХ<АВ.
22. У треугольника ABC угол С тупой. Докажите, что если точка X лежит на стороне АС, а точка Y — на стороне ВС,
то ХУ<АВ.
23. На стороне АВ треугольника ABC отмечена точка D.Докажите, что отрезок CD меньше по крайней мере одной из сторон: АС или ВС.
24*. Дан треугольник ABC. CD — медиана, проведенная к стороне АВ. Докажите, что если АС>ВС, то угол ACD меньше угла BCD.
25*. Докажите, что биссектриса треугольника не меньше высоты и не больше медианы, проведенных из этой же вершины.
26. Даны сторона и два угла треугольника. Найдите третий угол и остальные две стороны, если:
1) а = 5.  = 30°, = 30°, 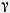 = 45°; = 45°;
2) а = 20,  = 75° = 75°  = 60°; = 60°;
3) a = 35,  = 40°, = 40°, 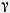 = 120°; = 120°;
4) b = 12,  = 36°, = 36°,  = 25°; = 25°;
5) с = 14.  = 64°. = 64°.  = 48°. = 48°.
27. Даны две стороны и угол между ними. Найдите остальные два угла и третью сторону, если:
1) a = 12, b = 8, 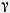 = 60°; = 60°;
2) а = 7. b = 23, 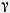 =130°; =130°;
3) b = 9, с=17.  = 95°; = 95°;
4) b = 14, с =10,  =145°; =145°;
5) а = 32. с = 23,  = 152°; = 152°;
6) a = 24, с = 18,  =15°. =15°.
28. В треугольнике заданы две стороны и угол, противолежащий одной из сторон. Найдите остальные углы и сторону треугольника, если:
1) а = 12. b = 5,  = 120° = 120°
2) а = 27, Ь = 9,  = 138°; = 138°;
3) a = 34, Ь = 12,  = 164°; = 164°;
4) а = 2. b = 4,  = 60°; = 60°;
5) а = 6. b = 8,  = 30°. = 30°.
29. Даны три стороны треугольника. Найдите его углы, если:
1) а = 2. b=г. с = 4;
2) а = 7. b = 2, с = 8;
3) а = 4. b = 5, с = 7;
4) a = 15, b = 24, с = 18;
5) a = 23, b = 17, с = 39;
6) а = 55, b = 21, с = 38.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Математика скачать, задача школьнику 9 класса, материалы по математике для 9 класса онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|











