|
|
|
| Строка 9: |
Строка 9: |
| | <br>'''''Ломаной А<sub>1</sub>А<sub>2</sub>А3 ... A<sub>n</sub> называется фигура, которая состоит из точек А<sub>1</sub>, А<sub>2</sub>, А<sub>n</sub> и соединяющих их отрезков A<sub>1</sub>,А<sub>2</sub>, А<sub>2</sub>,А<sub>3</sub>, А<sub>n-1</sub>,А<sub>n</sub>. Точки А<sub>1</sub>, А<sub>2</sub>, А<sub>n</sub> называются вершинами ломаной, а отрезки A<sub>1</sub>,А<sub>2</sub>, А<sub>2</sub>,А<sub>3</sub>, А<sub>n-1</sub>,А<sub>n</sub> — звеньями ломаной. Ломаная называется простой, если она не имеет самопересечений.''''' | | <br>'''''Ломаной А<sub>1</sub>А<sub>2</sub>А3 ... A<sub>n</sub> называется фигура, которая состоит из точек А<sub>1</sub>, А<sub>2</sub>, А<sub>n</sub> и соединяющих их отрезков A<sub>1</sub>,А<sub>2</sub>, А<sub>2</sub>,А<sub>3</sub>, А<sub>n-1</sub>,А<sub>n</sub>. Точки А<sub>1</sub>, А<sub>2</sub>, А<sub>n</sub> называются вершинами ломаной, а отрезки A<sub>1</sub>,А<sub>2</sub>, А<sub>2</sub>,А<sub>3</sub>, А<sub>n-1</sub>,А<sub>n</sub> — звеньями ломаной. Ломаная называется простой, если она не имеет самопересечений.''''' |
| | | | |
| - | '''''[[Image:24-06-71.jpg]]''''' На рисунке 273, а показана простая ломаная, а на рисунке 273, б — ломаная с самопересечением (в точке В). '''''Длиной ломаной называется сумма длин ее звеньев.''''' | + | '''''[[Image:24-06-71.jpg]]''''' |
| | + | |
| | + | |
| | + | |
| | + | На рисунке 273, а показана простая ломаная, а на рисунке 273, б — ломаная с самопересечением (в точке В). '''''Длиной ломаной называется сумма длин ее звеньев.''''' |
| | + | |
| | + | '' |
| | | | |
| | ''[[Image:24-06-72.jpg]]'' | | ''[[Image:24-06-72.jpg]]'' |
| | + | |
| | | | |
| | Теорема 13.1. '''''Длина ломаной не меньше длины отрезка, соединяющего ее концы.''''' | | Теорема 13.1. '''''Длина ломаной не меньше длины отрезка, соединяющего ее концы.''''' |
| Строка 22: |
Строка 29: |
| | | | |
| | Задача (1). Даны две окружности с радиусами R<sub>1</sub> и R<sub>2</sub> и расстоянием между центрами d>R<sub>1</sub>+R<sub>2</sub>. Чему равны наибольшее и наименьшее расстояния между точками X и Y этих окружностей? | | Задача (1). Даны две окружности с радиусами R<sub>1</sub> и R<sub>2</sub> и расстоянием между центрами d>R<sub>1</sub>+R<sub>2</sub>. Чему равны наибольшее и наименьшее расстояния между точками X и Y этих окружностей? |
| | + | |
| | + | |
| | | | |
| | [[Image:24-06-73.jpg]] | | [[Image:24-06-73.jpg]] |
| | + | |
| | + | |
| | | | |
| | Решение. Для ломаной 0<sub>1</sub>ХУ0<sub>2</sub> по теореме 13.1 O<sub>1</sub>O<sub>2</sub>[[Image:24-06-54.jpg]]O<sub>1</sub>X + XY + YO<sub>2</sub> (рис. 275). Значит, d[[Image:24-06-54.jpg]]R<sub>1</sub>+XY +R<sub>2</sub>. Отсюда XY[[Image:24-06-66.jpg]]R<sub>1</sub>—R<sub>2</sub>. Так как AC = d — R<sub>1</sub>—R<sub>2</sub>, то наименьшее расстояние между точками окружностей равно d — R<sub>1</sub>—R<sub>2</sub>. | | Решение. Для ломаной 0<sub>1</sub>ХУ0<sub>2</sub> по теореме 13.1 O<sub>1</sub>O<sub>2</sub>[[Image:24-06-54.jpg]]O<sub>1</sub>X + XY + YO<sub>2</sub> (рис. 275). Значит, d[[Image:24-06-54.jpg]]R<sub>1</sub>+XY +R<sub>2</sub>. Отсюда XY[[Image:24-06-66.jpg]]R<sub>1</sub>—R<sub>2</sub>. Так как AC = d — R<sub>1</sub>—R<sub>2</sub>, то наименьшее расстояние между точками окружностей равно d — R<sub>1</sub>—R<sub>2</sub>. |
Версия 12:53, 24 июня 2010
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика:Ломаная
ЛОМАНАЯ
Ломаной А1А2А3 ... An называется фигура, которая состоит из точек А1, А2, Аn и соединяющих их отрезков A1,А2, А2,А3, Аn-1,Аn. Точки А1, А2, Аn называются вершинами ломаной, а отрезки A1,А2, А2,А3, Аn-1,Аn — звеньями ломаной. Ломаная называется простой, если она не имеет самопересечений.
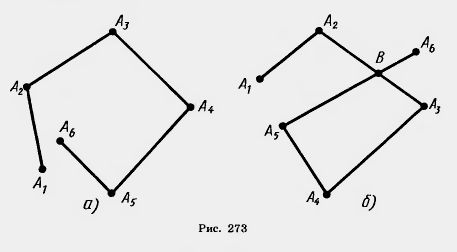
На рисунке 273, а показана простая ломаная, а на рисунке 273, б — ломаная с самопересечением (в точке В). Длиной ломаной называется сумма длин ее звеньев.
Теорема 13.1. Длина ломаной не меньше длины отрезка, соединяющего ее концы.
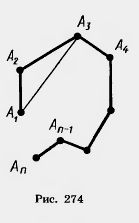
Доказательство. Пусть А1А2А3 ... An— данная ломаная (рис. 274).
Заменим звенья А1А2 и А2А3 одним звеном А1А3. Получим ломаную А1А3А4 ... An. Так как по неравенству треугольника
А1А3<А1А2 + А2А3, то ломаная A1A3A4 ... An имеет длину, не большую, чем исходная ломаная.
Заменяя таким же образом звенья А1А3 и А3А4 звеном А1А4, переходим к ломаной А1А4А5 ... Аn, которая также имеет длину, не большую, чем исходная ломаная. И т. д. В итоге мы придем к отрезку A1An соединяющему концы ломаной. Отсюда следует, что исходная ломаная имела длину, не меньшую длины отрезка A1An. Теорема доказана.
Задача (1). Даны две окружности с радиусами R1 и R2 и расстоянием между центрами d>R1+R2. Чему равны наибольшее и наименьшее расстояния между точками X и Y этих окружностей?
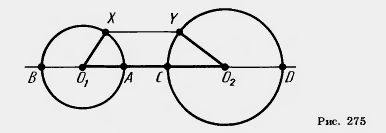
Решение. Для ломаной 01ХУ02 по теореме 13.1 O1O2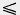 O1X + XY + YO2 (рис. 275). Значит, d O1X + XY + YO2 (рис. 275). Значит, d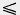 R1+XY +R2. Отсюда XY R1+XY +R2. Отсюда XY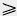 R1—R2. Так как AC = d — R1—R2, то наименьшее расстояние между точками окружностей равно d — R1—R2. R1—R2. Так как AC = d — R1—R2, то наименьшее расстояние между точками окружностей равно d — R1—R2.
Для ломаной ХО1О2У по той же теореме ХУ 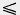 R1 +d +R2. Так как BD = d+R1 +R2, то наибольшее расстояние между точками окружностей равно d+R1 +R2,. R1 +d +R2. Так как BD = d+R1 +R2, то наибольшее расстояние между точками окружностей равно d+R1 +R2,.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Помощь школьнику онлайн, Математика для 9 класса скачать, календарно-тематическое планирование
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|













