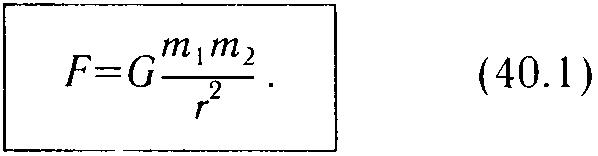|
|
|
| Строка 5: |
Строка 5: |
| | <metakeywords>Физика, 9 класс, Закон всемирного тяготения</metakeywords> | | <metakeywords>Физика, 9 класс, Закон всемирного тяготения</metakeywords> |
| | | | |
| - | В середине XVII в. многих ученых интересовал вопрос о том, как сила взаимного притяжения между телами зависит от расстояния между ними. С какой силой, например, Солнце притягивает к себе планеты? По поводу этого вопроса Р. Гук в 1674 г. писал: «Притягательные силы тем значительнее обнаруживают себя, чем ближе тело, на которое они действуют, находится от центра действия. В какой степени это увеличение зависит от расстояния, это я еще не определил опытом». Современникам Гука никак не удавалось найти выражение для силы тяготения и на его основе определить траектории планет. Правда, у Гука были на этот счет догадки, но доказать их он не мог.<br> В 1683 г. Гук специально встретился с учеными К. Реном и Э. Галлеем, интересовавшимися тем же вопросом, чтобы обсудить вместе с ними проблему тяготения. Но встреча этих трех ученых ни к чему не привела. Отчаявшийся Галлей обратился с этой задачей к Ньютону. Каково же было его удивление и радость, когда он узнал, что Ньютону уже давно известно ее решение!<br> Выражение для силы тяготения Ньютон получил еще в 1666 г., когда ему самому было всего лишь 24 года. Но в то время, сверяя результаты своей теории сданными опыта, он обнаружил расхождения и поэтому публиковать свои результаты не стал. В итоге открытый им закон оставался неизвестным людям в течение многих лет. Однако потом выяснилось, что данные, которыми он пользовался, были очень неточными. Когда же Ньютону стали известны результаты более точных измерений, он, как пишет О. Лодж, «достал свои старые рукописи и снова приступил к вычислениям... Новые данные изменяют результаты: в чрезвычайном возбуждении пересматривает он глазами свою работу, перо не успевает следить за мыслью, и наконец, вычисления приводят его к желаемым результатам. Беспредельно большое значение и глубина его открытия настолько ослепляют его своим сиянием, что затуманенные глаза не видят рукописи. В изнеможении он отбрасывает перо; тайна мироздания, наконец, открылась ему, единственному в мире...».<br> Сначала Ньютон установил, как зависит от расстояния ускорение свободного падения. Он заметил, что вблизи поверхности Земли, т. е. на расстоянии 6400 км от ее центра, это ускорение составляет 9,8 м/с2, а на расстоянии, в 60 раз большем, у Луны, это ускорение оказывается в 3600 раз меньше, чем на Земле. Значит, ускорение свободного падения убывает обратно пропорционально квадрату расстояния от центра Земли. Но ускорение по второму закону Ньютона пропорционально силе. Следовательно, причиной такого убывания ускорения является аналогичная зависимость от расстояния у силы тяготения.<br> Окончательную формулу силы тяготения можно получить, если учесть, что эта сила должна быть пропорциональна гравитационным зарядам взаимодействующих тел, т. е. их массам ''m1'' и ''m2''. Таким образом,<br> [[Image:tema40-1.jpg|center]] Так Ньютон нашел выражение для силы гравитационного взаимодействия Земли с притягиваемыми ею телами. Но интуиция подсказывала ему, что по полученной формуле можно рассчитывать и силу тяготения, действующую между любыми другими телами Вселенной, если только их размеры малы по сравнению с расстоянием r между ними. Поэтому он стал рассматривать полученное выражение как закон ''всемирного'' тяготения, справедливый и для небесных тел, и для тел, находящихся на Земле. Дальнейшее развитие науки показало, что Ньютон был прав и его закон действительно может быть применен к самым разным телам, начиная от атомов и молекул и кончая гигантскими звездными скоплениями.<br> Итак, '''закон всемирного тяготения''', открытый Ньютоном, гласит:<br> '''''Сила гравитационного притяжения любых двух частиц прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.'''''<br> Математически этот закон выражается формулой (40.1). Коэффициент пропорциональности ''G'' в этой формуле называется ''гравитационной постоянной''.<br> Закон всемирного тяготения сформулирован здесь для ''частиц'', т. е. для таких тел, размеры которых значительно меньше расстояния ''r'' между ними. Однако одна замечательная особенность этого закона позволяет использовать его и в некоторых других случаях. Такой особенностью является обратно пропорциональная зависимость силы тяготения именно от квадрата расстояния между частицами, а не от третьей, скажем, или четвертой степени расстояния. Расчеты показывают, что благодаря этому формулу (40.1) можно применять еще и для расчета силы притяжения ''шарообразных тел'' со сферически симметричным распределением вещества, находящихся на любом расстоянии друг от друга; только под ''r'' в этом случае следует понимать не расстояние между ними, а расстояние между их центрами (рис. 100). Справедливой оказывается формула (40.1) и в промежуточном случае, когда сферическое тело произвольного размера взаимодействует с некоторой материальной точкой. Это и дает возможность применять формулу закона всемирного тяготения для расчета силы, с которой земной шар притягивает к себе окружающие тела. | + | В середине XVII в. многих ученых интересовал вопрос о том, как сила взаимного притяжения между телами зависит от расстояния между ними. С какой силой, например, Солнце притягивает к себе планеты? По поводу этого вопроса Р. Гук в 1674 г. писал: «Притягательные силы тем значительнее обнаруживают себя, чем ближе тело, на которое они действуют, находится от центра действия. В какой степени это увеличение зависит от расстояния, это я еще не определил опытом». Современникам Гука никак не удавалось найти выражение для силы тяготения и на его основе определить траектории планет. Правда, у Гука были на этот счет догадки, но доказать их он не мог.<br> В 1683 г. Гук специально встретился с учеными К. Реном и Э. Галлеем, интересовавшимися тем же вопросом, чтобы обсудить вместе с ними проблему тяготения. Но встреча этих трех ученых ни к чему не привела. Отчаявшийся Галлей обратился с этой задачей к Ньютону. Каково же было его удивление и радость, когда он узнал, что Ньютону уже давно известно ее решение!<br> Выражение для силы тяготения Ньютон получил еще в 1666 г., когда ему самому было всего лишь 24 года. Но в то время, сверяя результаты своей теории сданными опыта, он обнаружил расхождения и поэтому публиковать свои результаты не стал. В итоге открытый им закон оставался неизвестным людям в течение многих лет. Однако потом выяснилось, что данные, которыми он пользовался, были очень неточными. Когда же Ньютону стали известны результаты более точных измерений, он, как пишет О. Лодж, «достал свои старые рукописи и снова приступил к вычислениям... Новые данные изменяют результаты: в чрезвычайном возбуждении пересматривает он глазами свою работу, перо не успевает следить за мыслью, и наконец, вычисления приводят его к желаемым результатам. Беспредельно большое значение и глубина его открытия настолько ослепляют его своим сиянием, что затуманенные глаза не видят рукописи. В изнеможении он отбрасывает перо; тайна мироздания, наконец, открылась ему, единственному в мире...».<br> Сначала Ньютон установил, как зависит от расстояния ускорение свободного падения. Он заметил, что вблизи поверхности Земли, т. е. на расстоянии 6400 км от ее центра, это ускорение составляет 9,8 м/с2, а на расстоянии, в 60 раз большем, у Луны, это ускорение оказывается в 3600 раз меньше, чем на Земле. Значит, ускорение свободного падения убывает обратно пропорционально квадрату расстояния от центра Земли. Но ускорение по второму закону Ньютона пропорционально силе. Следовательно, причиной такого убывания ускорения является аналогичная зависимость от расстояния у силы тяготения.<br> Окончательную формулу силы тяготения можно получить, если учесть, что эта сила должна быть пропорциональна гравитационным зарядам взаимодействующих тел, т. е. их массам ''m1'' и ''m2''. Таким образом,<br> [[Image:Tema40-1.jpg|center|259x67px]] Так Ньютон нашел выражение для силы гравитационного взаимодействия Земли с притягиваемыми ею телами. Но интуиция подсказывала ему, что по полученной формуле можно рассчитывать и силу тяготения, действующую между любыми другими телами Вселенной, если только их размеры малы по сравнению с расстоянием r между ними. Поэтому он стал рассматривать полученное выражение как закон ''всемирного'' тяготения, справедливый и для небесных тел, и для тел, находящихся на Земле. Дальнейшее развитие науки показало, что Ньютон был прав и его закон действительно может быть применен к самым разным телам, начиная от атомов и молекул и кончая гигантскими звездными скоплениями.<br> Итак, '''закон всемирного тяготения''', открытый Ньютоном, гласит:<br> '''''Сила гравитационного притяжения любых двух частиц прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.'''''<br> Математически этот закон выражается формулой (40.1). Коэффициент пропорциональности ''G'' в этой формуле называется ''гравитационной постоянной''.<br> Закон всемирного тяготения сформулирован здесь для ''частиц'', т. е. для таких тел, размеры которых значительно меньше расстояния ''r'' между ними. Однако одна замечательная особенность этого закона позволяет использовать его и в некоторых других случаях. Такой особенностью является обратно пропорциональная зависимость силы тяготения именно от квадрата расстояния между частицами, а не от третьей, скажем, или четвертой степени расстояния. Расчеты показывают, что благодаря этому формулу (40.1) можно применять еще и для расчета силы притяжения ''шарообразных тел'' со сферически симметричным распределением вещества, находящихся на любом расстоянии друг от друга; только под ''r'' в этом случае следует понимать не расстояние между ними, а расстояние между их центрами (рис. 100). Справедливой оказывается формула (40.1) и в промежуточном случае, когда сферическое тело произвольного размера взаимодействует с некоторой материальной точкой. Это и дает возможность применять формулу закона всемирного тяготения для расчета силы, с которой земной шар притягивает к себе окружающие тела. |
| | | | |
| - | [[Image:f100.jpg|center]] Согласно легенде, мысль о всемирном тяготении осенила Ньютона в тот момент, когда он, отдыхая в своем саду, увидел падающее яблоко. Рассказывают даже, что знаменитой яблоне, чей плод сумел так вовремя упасть к ногам Ньютона, не дали исчезнуть без следа и кусочки этого дерева якобы хранятся в Англии до сих пор.<br> Открытие закона всемирного тяготения позволило Ньютону создать теорию движения небесных тел, основанную на строгих математических доказательствах. Ничего подобного в науке до этого не было. Однако сильное впечатление, произведенное этой теорией на современников Ньютона, не помешало появлению у них некоторого чувства неудовлетворенности. Всех тогда интересовал вопрос «почему?»: почему все тела притягиваются друг к другу? Ньютон ответа на этот вопрос не дал. «Причину же свойств силы тяготения я до сих пор не мог вывести из явлений, гипотез же я не измышляю,- писал он в своих «Математических началах».- Довольно того, что тяготение на самом деле существует и действует согласно изложенным нами законам и вполне достаточно для объяснения всех движений небесных тел и моря».<br> Говоря о море, Ньютон подразумевал явление приливов, которые обусловлены притяжением воды Луной и Солнцем. За две тысячи лет до Ньютона над причинами этого явления размышлял Аристотель, которому, однако, решить эту проблему не удалось. Для Аристотеля это явилось трагедией. «Наблюдая длительное время это явление со скалы Негропонта, он, охваченный отчаянием, бросился в море и нашел там добровольную смерть» (Г. Галилей).<br> | + | [[Image:F100.jpg|center|275x179px]] Согласно легенде, мысль о всемирном тяготении осенила Ньютона в тот момент, когда он, отдыхая в своем саду, увидел падающее яблоко. Рассказывают даже, что знаменитой яблоне, чей плод сумел так вовремя упасть к ногам Ньютона, не дали исчезнуть без следа и кусочки этого дерева якобы хранятся в Англии до сих пор.<br> Открытие закона всемирного тяготения позволило Ньютону создать теорию движения небесных тел, основанную на строгих математических доказательствах. Ничего подобного в науке до этого не было. Однако сильное впечатление, произведенное этой теорией на современников Ньютона, не помешало появлению у них некоторого чувства неудовлетворенности. Всех тогда интересовал вопрос «почему?»: почему все тела притягиваются друг к другу? Ньютон ответа на этот вопрос не дал. «Причину же свойств силы тяготения я до сих пор не мог вывести из явлений, гипотез же я не измышляю,- писал он в своих «Математических началах».- Довольно того, что тяготение на самом деле существует и действует согласно изложенным нами законам и вполне достаточно для объяснения всех движений небесных тел и моря».<br> Говоря о море, Ньютон подразумевал явление приливов, которые обусловлены притяжением воды Луной и Солнцем. За две тысячи лет до Ньютона над причинами этого явления размышлял Аристотель, которому, однако, решить эту проблему не удалось. Для Аристотеля это явилось трагедией. «Наблюдая длительное время это явление со скалы Негропонта, он, охваченный отчаянием, бросился в море и нашел там добровольную смерть» (Г. Галилей).<br> |
| | | | |
| | + | <br> |
| | | | |
| | + | ??? <br> 1. Сформулируйте закон всемирного тяготения. Для каких тел он справедлив? <br> 2. Что следует понимать под ''r'' в формуле (40.1) при расчете силы гравитационного взаимодействия шаров? <br> 3. Как называется коэффициент пропорциональности ''G'' в законе всемирного тяготения?<br> |
| | | | |
| - | ??? <br> 1. Сформулируйте закон всемирного тяготения. Для каких тел он справедлив? <br> 2. Что следует понимать под ''r'' в формуле (40.1) при расчете силы гравитационного взаимодействия шаров? <br> 3. Как называется коэффициент пропорциональности ''G'' в законе всемирного тяготения?<br>
| + | <br> ''С.В. Громов, И.А. Родина, Физика 9 класс'' |
| - | | + | |
| - | | + | |
| - | ''С.В. Громов, И.А. Родина, Физика 9 класс'' | + | |
| | | | |
| | <br> <sub>Планирования [[Физика и астрономия|по физике]], учебники и книги онлайн, курсы и задания [[Физика 9 класс|по физике для 9 класса]]</sub> | | <br> <sub>Планирования [[Физика и астрономия|по физике]], учебники и книги онлайн, курсы и задания [[Физика 9 класс|по физике для 9 класса]]</sub> |
Версия 20:02, 28 июня 2010
Гипермаркет знаний>>Физика и астрономия>>Физика 9 класс>>Физика: Закон всемирного тяготения
В середине XVII в. многих ученых интересовал вопрос о том, как сила взаимного притяжения между телами зависит от расстояния между ними. С какой силой, например, Солнце притягивает к себе планеты? По поводу этого вопроса Р. Гук в 1674 г. писал: «Притягательные силы тем значительнее обнаруживают себя, чем ближе тело, на которое они действуют, находится от центра действия. В какой степени это увеличение зависит от расстояния, это я еще не определил опытом». Современникам Гука никак не удавалось найти выражение для силы тяготения и на его основе определить траектории планет. Правда, у Гука были на этот счет догадки, но доказать их он не мог.
В 1683 г. Гук специально встретился с учеными К. Реном и Э. Галлеем, интересовавшимися тем же вопросом, чтобы обсудить вместе с ними проблему тяготения. Но встреча этих трех ученых ни к чему не привела. Отчаявшийся Галлей обратился с этой задачей к Ньютону. Каково же было его удивление и радость, когда он узнал, что Ньютону уже давно известно ее решение!
Выражение для силы тяготения Ньютон получил еще в 1666 г., когда ему самому было всего лишь 24 года. Но в то время, сверяя результаты своей теории сданными опыта, он обнаружил расхождения и поэтому публиковать свои результаты не стал. В итоге открытый им закон оставался неизвестным людям в течение многих лет. Однако потом выяснилось, что данные, которыми он пользовался, были очень неточными. Когда же Ньютону стали известны результаты более точных измерений, он, как пишет О. Лодж, «достал свои старые рукописи и снова приступил к вычислениям... Новые данные изменяют результаты: в чрезвычайном возбуждении пересматривает он глазами свою работу, перо не успевает следить за мыслью, и наконец, вычисления приводят его к желаемым результатам. Беспредельно большое значение и глубина его открытия настолько ослепляют его своим сиянием, что затуманенные глаза не видят рукописи. В изнеможении он отбрасывает перо; тайна мироздания, наконец, открылась ему, единственному в мире...».
Сначала Ньютон установил, как зависит от расстояния ускорение свободного падения. Он заметил, что вблизи поверхности Земли, т. е. на расстоянии 6400 км от ее центра, это ускорение составляет 9,8 м/с2, а на расстоянии, в 60 раз большем, у Луны, это ускорение оказывается в 3600 раз меньше, чем на Земле. Значит, ускорение свободного падения убывает обратно пропорционально квадрату расстояния от центра Земли. Но ускорение по второму закону Ньютона пропорционально силе. Следовательно, причиной такого убывания ускорения является аналогичная зависимость от расстояния у силы тяготения.
Окончательную формулу силы тяготения можно получить, если учесть, что эта сила должна быть пропорциональна гравитационным зарядам взаимодействующих тел, т. е. их массам m1 и m2. Таким образом,
Так Ньютон нашел выражение для силы гравитационного взаимодействия Земли с притягиваемыми ею телами. Но интуиция подсказывала ему, что по полученной формуле можно рассчитывать и силу тяготения, действующую между любыми другими телами Вселенной, если только их размеры малы по сравнению с расстоянием r между ними. Поэтому он стал рассматривать полученное выражение как закон всемирного тяготения, справедливый и для небесных тел, и для тел, находящихся на Земле. Дальнейшее развитие науки показало, что Ньютон был прав и его закон действительно может быть применен к самым разным телам, начиная от атомов и молекул и кончая гигантскими звездными скоплениями.
Итак, закон всемирного тяготения, открытый Ньютоном, гласит:
Сила гравитационного притяжения любых двух частиц прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.
Математически этот закон выражается формулой (40.1). Коэффициент пропорциональности G в этой формуле называется гравитационной постоянной.
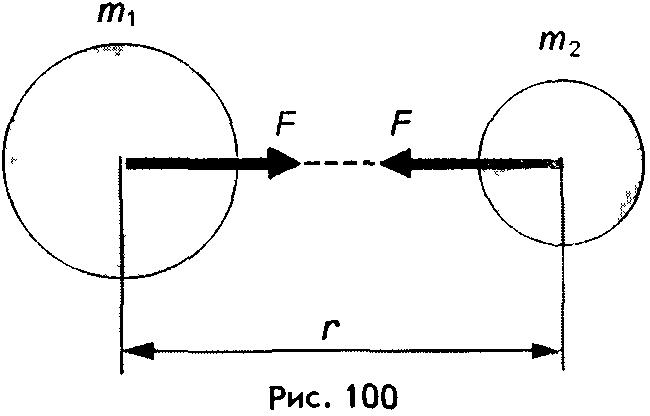
Закон всемирного тяготения сформулирован здесь для частиц, т. е. для таких тел, размеры которых значительно меньше расстояния r между ними. Однако одна замечательная особенность этого закона позволяет использовать его и в некоторых других случаях. Такой особенностью является обратно пропорциональная зависимость силы тяготения именно от квадрата расстояния между частицами, а не от третьей, скажем, или четвертой степени расстояния. Расчеты показывают, что благодаря этому формулу (40.1) можно применять еще и для расчета силы притяжения шарообразных тел со сферически симметричным распределением вещества, находящихся на любом расстоянии друг от друга; только под r в этом случае следует понимать не расстояние между ними, а расстояние между их центрами (рис. 100). Справедливой оказывается формула (40.1) и в промежуточном случае, когда сферическое тело произвольного размера взаимодействует с некоторой материальной точкой. Это и дает возможность применять формулу закона всемирного тяготения для расчета силы, с которой земной шар притягивает к себе окружающие тела.
Согласно легенде, мысль о всемирном тяготении осенила Ньютона в тот момент, когда он, отдыхая в своем саду, увидел падающее яблоко. Рассказывают даже, что знаменитой яблоне, чей плод сумел так вовремя упасть к ногам Ньютона, не дали исчезнуть без следа и кусочки этого дерева якобы хранятся в Англии до сих пор.
Открытие закона всемирного тяготения позволило Ньютону создать теорию движения небесных тел, основанную на строгих математических доказательствах. Ничего подобного в науке до этого не было. Однако сильное впечатление, произведенное этой теорией на современников Ньютона, не помешало появлению у них некоторого чувства неудовлетворенности. Всех тогда интересовал вопрос «почему?»: почему все тела притягиваются друг к другу? Ньютон ответа на этот вопрос не дал. «Причину же свойств силы тяготения я до сих пор не мог вывести из явлений, гипотез же я не измышляю,- писал он в своих «Математических началах».- Довольно того, что тяготение на самом деле существует и действует согласно изложенным нами законам и вполне достаточно для объяснения всех движений небесных тел и моря».
Говоря о море, Ньютон подразумевал явление приливов, которые обусловлены притяжением воды Луной и Солнцем. За две тысячи лет до Ньютона над причинами этого явления размышлял Аристотель, которому, однако, решить эту проблему не удалось. Для Аристотеля это явилось трагедией. «Наблюдая длительное время это явление со скалы Негропонта, он, охваченный отчаянием, бросился в море и нашел там добровольную смерть» (Г. Галилей).
???
1. Сформулируйте закон всемирного тяготения. Для каких тел он справедлив?
2. Что следует понимать под r в формуле (40.1) при расчете силы гравитационного взаимодействия шаров?
3. Как называется коэффициент пропорциональности G в законе всемирного тяготения?
С.В. Громов, И.А. Родина, Физика 9 класс
Планирования по физике, учебники и книги онлайн, курсы и задания по физике для 9 класса
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|