|
|
|
| Строка 1: |
Строка 1: |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Способы задания функции<metakeywords>Способы задания функции</metakeywords>''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Способы задания функции<metakeywords>Способы задания функции</metakeywords>''' |
| | + | |
| | + | <br> |
| | + | |
| | + | '''СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ'''<br>Приводя в предыдущем параграфе различные примеры функций, мы несколько обеднили само понятие функции. Ведь задать функцию — это значит указать правило, которое позволяет по произвольно выбранному значению х из Б(0 вычислить соответствующее значение у. Чаще всего это правило связано с формулой или с несколькими формулами — такой способ задания функции обычно называют аналитическим. Все функции, рассмотренные в § 7, были заданы аналитически. Между тем есть другие способы задания функции, о них и пойдет речь в настоящем параграфе.<br>Пусть F — некоторая линия на координатной плоскости и пусть, спроецировав эту линию на ось х, мы получим отрезок [a, b] (рис. 50). Возьмем произвольную точку х из отрезка [a, b] и проведем через нее прямую, параллельную оси ординат. Потребуем дополнительно, чтобы каждая такая прямая пересекала линию M только в одной точке — на рис. 50 соответствующая точка обозначена буквой М. Ордината точки М — это число f(х), соответствующее выбранному значению х. Тем самым на отрезке [a, b] задана функция у — f(х). Такой способ задания функции называют графическим, а линию F — графиком функции.<br>Если функция была задана аналитически и нам удалось построить график функции, то мы фактически перешли от аналитического способа задания функции к графическому. Обратный же переход удается осуществить далеко не всегда. Как правило, это довольно трудная, но интересная задача.<br>Не всякая линия на координатной плоскости может рассматриваться как график некоторой функции. Например, окружность, заданная уравнением х<sup>2</sup> + у<sup>2</sup> — 9 (рис. 51), не является графиком функции, поскольку любая прямая х = а, где | а | <3, пересекает эту линию в д в у х точках (а для задания функции таких точек должно быть не более одной, т.е. прямая х = а должна пересекать линию F только в одной точке либо вообще не должна ее пересекать). В то же время если эту окружность разрезать на две части — верхнюю полуокружность (рис. 52) и нижнюю полуокружность (рис. 53), — то каждую из |
| | + | |
| | + | [[Image:al91.jpg]] |
| | + | |
| | + | полуокружностей можно считать графиком некоторой функции, причем в обоих случаях несложно от графического способа задания функции перейти к аналитическому. Из уравнения х<sup>2</sup> + у<sup>2</sup> = 9 находим у2 = 9 - х<sup>2</sup> и далее [[Image:al92.jpg]] Графиком функции [[Image:al93.jpg]] является верхняя полуокружность окружности х<sup>2</sup>+ у<sup>2</sup> =9 (рис. 52), а графиком функции [[Image:al94.jpg]] является нижняя полуокружность окружности х<sup>2</sup> + у<sup>2</sup> = 9 (рис. 53). |
| | + | |
| | + | [[Image:al95.jpg]] <br>Этот пример позволяет обратить внимание на одно существенное обстоятельство. Посмотрите на график функции [[Image:al93.jpg]] (рис. 52). Сразу ясно, что D(f) = [-3, 3]. А если бы речь шла об отыскании области определения аналитически заданной функции [[Image:al96.jpg]] Тогда пришлось бы, как мы это делали в § 7, тратить время и силы на решение неравенства [[Image:al97.jpg]] Потому-то обычно и стараются работать одновременно и с аналитическим, и с графическим способами задания функций. Впрочем, за два года изучения курса алгебры в школе вы к этому уже привыкли.<br>Кроме аналитического и графического, на практике применяют табличный способ задания функции. При этом способе приводится таблица, в которой указаны значения функции (иногда точные, иногда приближенные) для конечного множества значений аргумента. Примерами табличного задания функции могут служить таблицы квадратов чисел, кубов чисел, квадратных корней и т.д.<br> |
| | + | |
| | + | Во многих случаях табличное задание функции способы зада- является удобным. Оно позволяет найти значение *н*литичГ" ФУНКЦИИ Для имеющихся в таблице значений аргу-ский мента без всяких вычислений.<br>графический, Аналитический, графический, табличный — наитабличный, более простые, а потому наиболее популярные спо-словесный собы задания функции, для наших нужд этих способов вполне достаточно. На самом деле в математике имеется довольно много различных способов задания функции, но мы познакомим вас еще только с одним способом, который используется в весьма своеобразных ситуациях. Речь идет о словесном способе, когда правило задания функции описывается словами. Приведем примеры.<br>Пример 1. Функция у = {(х) задана на множестве всех неотрицательных чисел с помощью следующего правила: каждому числу х > 0 ставится в соответствие первый знак после запятой в десятичной записи числа х. Если, скажем, х = 2,534, то /(х) = 5 (первый знак после запятой — цифра 5); если х = 13,002, то 2 2<br>/(х) = 0; если х = - , то, записав - в виде бесконечной десятичной<br>дроби 0,6666..., находим /(х) = 6. А чему равно значение /(15)? Оно равно 0, так как 15 = 15,000... , и мы видим, что первый десятичный знак после запятой есть 0 (вообще-то верно и равенство 15 = 14,999... , но математики договорились не рассматривать бесконечные периодические десятичные дроби с периодом 9).<br>Любое неотрицательное число х можно записать в виде десятичной дроби (конечной или бесконечной), а потому для каждого значения х можно найти определенное значение первого знака после запятой, так что мы можем говорить о функции, хотя и несколько необычной. У этой функции<br>Ж/) = [0,+оо), Е(/) = {0, 1,2,3,4,5,6, 7,8,9}. (В<br>Пример 2. Функция у = /(х) задана на множестве всех действительных чисел с помощью следующего правила: каждому чис-<br>74<br>».9. I<br>ЧИСЛОВЫЕ ФУНКЦИИ<br>лу х ставится в соответствие наибольшее из всех целых чисел, которые не превосходят х. Иными словами, функция у = /(х) определяется следующими условиями:<br>а) /(х) — целое число;<br>б) /(х) < х (поскольку /(х) не превосходит х);<br>в) /(х) + 1 > х (поскольку /(х) — наибольшее целое число, не превосходящее х, значит, /(х) + 1 уже больше, чем х). Если, скажем, х = 2,534, то /(х) = 2, поскольку, во-первых, 2 — целое число, во-вторых, 2 < 2,534 и, в-третьих, следующее целое число 3 уже больше, чем 2,534. Если х = 47, то /(х) = 47, поскольку, во-первых, 47 — целое число, во-вторых, 47< 47 (точнее, 47 = 47) и, в-третьих, следующее за числом 47 целое число 48 уже больше, чем 47. А чему равно значение /(-0,(23))? Оно равно -1. Проверяйте: -1 — наибольшее из всех целых чисел, которые не превосходят числа -0,232323....<br>У этой функции !>(/) = (-оо, +оо), а Е(/) = 2 (множество целых чисел). (И<br>Функцию, о которой шла речь в примере 2, называют целой частью числа; для целой части числа х используют обозначение [х]. Например, [2,534] = 2, [47] = 47, [-0,(23)] = -1. Очень своеобразно выглядит график функции у = [х] (рис. 54).<br> ^ 5 1У <br> 4 <br> Я <br> 9 <br> 1 <br> X<br> -4 -3 -2 -1 0 1 2 3 4 о<br> -1 <br> -2 <br> -3 <br> -4 <br>Рис. 80а Рис. 806<br>75<br>3.12. ||<br>ЧИСЛОВЫЕ ФУНКЦИИ<br> |
| | + | |
| | + | <br> |
| | | | |
| | А.Г. Мордкович Алгебра 9 класс | | А.Г. Мордкович Алгебра 9 класс |
Версия 11:54, 29 июня 2010
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Способы задания функции
СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ
Приводя в предыдущем параграфе различные примеры функций, мы несколько обеднили само понятие функции. Ведь задать функцию — это значит указать правило, которое позволяет по произвольно выбранному значению х из Б(0 вычислить соответствующее значение у. Чаще всего это правило связано с формулой или с несколькими формулами — такой способ задания функции обычно называют аналитическим. Все функции, рассмотренные в § 7, были заданы аналитически. Между тем есть другие способы задания функции, о них и пойдет речь в настоящем параграфе.
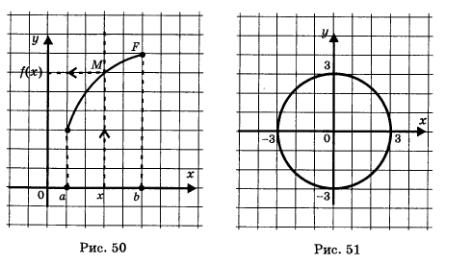
Пусть F — некоторая линия на координатной плоскости и пусть, спроецировав эту линию на ось х, мы получим отрезок [a, b] (рис. 50). Возьмем произвольную точку х из отрезка [a, b] и проведем через нее прямую, параллельную оси ординат. Потребуем дополнительно, чтобы каждая такая прямая пересекала линию M только в одной точке — на рис. 50 соответствующая точка обозначена буквой М. Ордината точки М — это число f(х), соответствующее выбранному значению х. Тем самым на отрезке [a, b] задана функция у — f(х). Такой способ задания функции называют графическим, а линию F — графиком функции.
Если функция была задана аналитически и нам удалось построить график функции, то мы фактически перешли от аналитического способа задания функции к графическому. Обратный же переход удается осуществить далеко не всегда. Как правило, это довольно трудная, но интересная задача.
Не всякая линия на координатной плоскости может рассматриваться как график некоторой функции. Например, окружность, заданная уравнением х2 + у2 — 9 (рис. 51), не является графиком функции, поскольку любая прямая х = а, где | а | <3, пересекает эту линию в д в у х точках (а для задания функции таких точек должно быть не более одной, т.е. прямая х = а должна пересекать линию F только в одной точке либо вообще не должна ее пересекать). В то же время если эту окружность разрезать на две части — верхнюю полуокружность (рис. 52) и нижнюю полуокружность (рис. 53), — то каждую из
полуокружностей можно считать графиком некоторой функции, причем в обоих случаях несложно от графического способа задания функции перейти к аналитическому. Из уравнения х2 + у2 = 9 находим у2 = 9 - х2 и далее 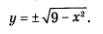 Графиком функции Графиком функции 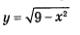 является верхняя полуокружность окружности х2+ у2 =9 (рис. 52), а графиком функции является верхняя полуокружность окружности х2+ у2 =9 (рис. 52), а графиком функции 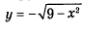 является нижняя полуокружность окружности х2 + у2 = 9 (рис. 53). является нижняя полуокружность окружности х2 + у2 = 9 (рис. 53).
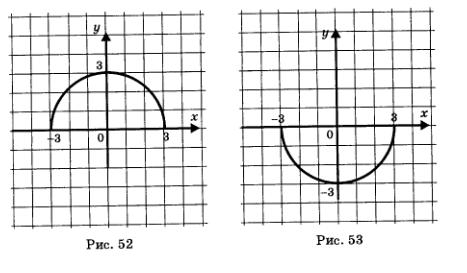
Этот пример позволяет обратить внимание на одно существенное обстоятельство. Посмотрите на график функции 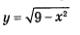 (рис. 52). Сразу ясно, что D(f) = [-3, 3]. А если бы речь шла об отыскании области определения аналитически заданной функции (рис. 52). Сразу ясно, что D(f) = [-3, 3]. А если бы речь шла об отыскании области определения аналитически заданной функции 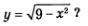 Тогда пришлось бы, как мы это делали в § 7, тратить время и силы на решение неравенства Тогда пришлось бы, как мы это делали в § 7, тратить время и силы на решение неравенства 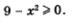 Потому-то обычно и стараются работать одновременно и с аналитическим, и с графическим способами задания функций. Впрочем, за два года изучения курса алгебры в школе вы к этому уже привыкли. Потому-то обычно и стараются работать одновременно и с аналитическим, и с графическим способами задания функций. Впрочем, за два года изучения курса алгебры в школе вы к этому уже привыкли.
Кроме аналитического и графического, на практике применяют табличный способ задания функции. При этом способе приводится таблица, в которой указаны значения функции (иногда точные, иногда приближенные) для конечного множества значений аргумента. Примерами табличного задания функции могут служить таблицы квадратов чисел, кубов чисел, квадратных корней и т.д.
Во многих случаях табличное задание функции способы зада- является удобным. Оно позволяет найти значение *н*литичГ" ФУНКЦИИ Для имеющихся в таблице значений аргу-ский мента без всяких вычислений.
графический, Аналитический, графический, табличный — наитабличный, более простые, а потому наиболее популярные спо-словесный собы задания функции, для наших нужд этих способов вполне достаточно. На самом деле в математике имеется довольно много различных способов задания функции, но мы познакомим вас еще только с одним способом, который используется в весьма своеобразных ситуациях. Речь идет о словесном способе, когда правило задания функции описывается словами. Приведем примеры.
Пример 1. Функция у = {(х) задана на множестве всех неотрицательных чисел с помощью следующего правила: каждому числу х > 0 ставится в соответствие первый знак после запятой в десятичной записи числа х. Если, скажем, х = 2,534, то /(х) = 5 (первый знак после запятой — цифра 5); если х = 13,002, то 2 2
/(х) = 0; если х = - , то, записав - в виде бесконечной десятичной
дроби 0,6666..., находим /(х) = 6. А чему равно значение /(15)? Оно равно 0, так как 15 = 15,000... , и мы видим, что первый десятичный знак после запятой есть 0 (вообще-то верно и равенство 15 = 14,999... , но математики договорились не рассматривать бесконечные периодические десятичные дроби с периодом 9).
Любое неотрицательное число х можно записать в виде десятичной дроби (конечной или бесконечной), а потому для каждого значения х можно найти определенное значение первого знака после запятой, так что мы можем говорить о функции, хотя и несколько необычной. У этой функции
Ж/) = [0,+оо), Е(/) = {0, 1,2,3,4,5,6, 7,8,9}. (В
Пример 2. Функция у = /(х) задана на множестве всех действительных чисел с помощью следующего правила: каждому чис-
74
».9. I
ЧИСЛОВЫЕ ФУНКЦИИ
лу х ставится в соответствие наибольшее из всех целых чисел, которые не превосходят х. Иными словами, функция у = /(х) определяется следующими условиями:
а) /(х) — целое число;
б) /(х) < х (поскольку /(х) не превосходит х);
в) /(х) + 1 > х (поскольку /(х) — наибольшее целое число, не превосходящее х, значит, /(х) + 1 уже больше, чем х). Если, скажем, х = 2,534, то /(х) = 2, поскольку, во-первых, 2 — целое число, во-вторых, 2 < 2,534 и, в-третьих, следующее целое число 3 уже больше, чем 2,534. Если х = 47, то /(х) = 47, поскольку, во-первых, 47 — целое число, во-вторых, 47< 47 (точнее, 47 = 47) и, в-третьих, следующее за числом 47 целое число 48 уже больше, чем 47. А чему равно значение /(-0,(23))? Оно равно -1. Проверяйте: -1 — наибольшее из всех целых чисел, которые не превосходят числа -0,232323....
У этой функции !>(/) = (-оо, +оо), а Е(/) = 2 (множество целых чисел). (И
Функцию, о которой шла речь в примере 2, называют целой частью числа; для целой части числа х используют обозначение [х]. Например, [2,534] = 2, [47] = 47, [-0,(23)] = -1. Очень своеобразно выглядит график функции у = [х] (рис. 54).
^ 5 1У
4
Я
9
1
X
-4 -3 -2 -1 0 1 2 3 4 о
-1
-2
-3
-4
Рис. 80а Рис. 806
75
3.12. ||
ЧИСЛОВЫЕ ФУНКЦИИ
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|












