|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Геометрия, урок, на Тему, Площадь параллелограмма</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Геометрия, урок, на Тему, Площадь параллелограмма, параллелограмм, перпендикуляр, площадь</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Площадь параллелограмма''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Площадь параллелограмма''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
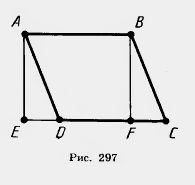
| - | ''' ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА'''<br> <br><br>Пусть ABCD — данный параллелограмм. Если он не является прямоугольником, то один из его углов — А или В — острый. Пусть для определенности угол А острый, как изображено на рисунке 297. | + | '''Площадь параллелограмма''' <br><br>Пусть ABCD — данный [[Паралелограм. Ознаки паралелограма. Властивості паралелограма|параллелограмм]]. Если он не является прямоугольником, то один из его углов — А или В — острый. Пусть для определенности угол А острый, как изображено на рисунке 297. |
| | | | |
| - | Опустим перпендикуляр АЕ из вершины А на прямую CD. Площадь трапеции АВСЕ равна сумме площадей параллелограмма ABCD и треугольника ADE.<br> | + | Опустим [[Паралельні та перпендикулярні прямі|перпендикуляр]] АЕ из вершины А на прямую CD. Площадь трапеции АВСЕ равна сумме площадей параллелограмма ABCD и треугольника ADE.<br> |
| | | | |
| - | Опустим перпендикуляр BF из вершины В на прямую CD. Тогда площадь трапеции АВСЕ равна сумме площадей прямоугольника ABFE и треугольника ВСЕ.<br>Прямоугольные треугольники ADE и ВСЕ равны, а значит, имеют равные площади. Отсюда следует, что площадь параллелограмма ABCD равна площади прямоугольника ABFE, т. е. равна ABBF. | + | Опустим перпендикуляр BF из вершины В на прямую CD. Тогда площадь трапеции АВСЕ равна сумме площадей прямоугольника ABFE и треугольника ВСЕ. |
| | | | |
| - | Отрезок BF называется'''''высотой параллелограмма''''', соответствующей сторонам АВ и CD.
| + | Прямоугольные треугольники ADE и ВСЕ равны, а значит, имеют равные площади. Отсюда следует, что [[Понятие площади|площадь]] параллелограмма ABCD равна площади прямоугольника ABFE, т. е. равна ABBF. |
| | | | |
| - | '''''Итак, площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой<br>стороне. ''''' Рис. 297
| + | Отрезок BF называется высотой параллелограмма, соответствующей сторонам АВ и CD. |
| | + | |
| | + | Итак, площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой<br>стороне. Рис. 297 |
| | + | |
| | + | [[Image:29-06-28.jpg|180px|Площадь параллелограмма ]] |
| | + | |
| | + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | [[Image:29-06-28.jpg]]<br>
| |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Полный перечень тем по классам, календарный план согласно школьной программе по математике [[Гипермаркет знаний - первый в мире!|онлайн]], видеоматериал по математике для 9 класса [[Математика|скачать]]</sub> | | <sub>Полный перечень тем по классам, календарный план согласно школьной программе по математике [[Гипермаркет знаний - первый в мире!|онлайн]], видеоматериал по математике для 9 класса [[Математика|скачать]]</sub> |
| Строка 24: |
Строка 28: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Опустим перпендикуляр BF из вершины В на прямую CD. Тогда площадь трапеции АВСЕ равна сумме площадей прямоугольника ABFE и треугольника ВСЕ.
Прямоугольные треугольники ADE и ВСЕ равны, а значит, имеют равные площади. Отсюда следует, что площадь параллелограмма ABCD равна площади прямоугольника ABFE, т. е. равна ABBF.
Отрезок BF называется высотой параллелограмма, соответствующей сторонам АВ и CD.
Итак, площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой
стороне. Рис. 297
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.