|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Геометрия, урок, на Тему, Подобие правильных выпуклых многоугольников</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Геометрия, урок, на Тему, Подобие правильных выпуклых многоугольников, теоремы, Треугольники, многоугольник, преобразованию подобия, коэффициент</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Подобие правильных выпуклых многоугольников''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Подобие правильных выпуклых многоугольников''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | '''ПОДОБИЕ ПРАВИЛЬНЫХ ВЫПУКЛЫХ МНОГОУГОЛЬНИКОВ'''
| + | '''Подобие правильных выпуклых многоугольников''' |
| | | | |
| - | <br>Теорема 13.4. '''''Правильные выпуклые п-угольники подобны. В частности, если у них стороны одинаковы, то они равны'''''. | + | '''<br>Теорема 13.4.''' Правильные выпуклые n-угольники подобны. В частности, если у них стороны одинаковы, то они равны. |
| | | | |
| - | Доказательство. Докажем сначала второе утверждение теоремы. Итак, пусть Р<sub>1</sub>: А<sub>1</sub>А<sub>2</sub>...А<sub>n</sub>, P<sub>2</sub>: B<sub>1</sub>B<sub>2</sub>...B<sub>n</sub> — правильные выпуклые n-угольники с одинаковыми сторонами (рис. 287). Докажем, что они равны, т. е. совмещаются движением. | + | '''Доказательство'''. Докажем сначала второе утверждение [[Теоремы и доказательства|теоремы]]. Итак, пусть Р<sub>1</sub>: А<sub>1</sub>А<sub>2</sub>...А<sub>n</sub>, P<sub>2</sub>: B<sub>1</sub>B<sub>2</sub>...B<sub>n</sub> — правильные выпуклые n-угольники с одинаковыми сторонами (рис. 287). Докажем, что они равны, т. е. совмещаются движением. |
| | | | |
| - | Треугольники А<sub>1</sub>А<sub>2</sub>А<sub>3</sub> и В<sub>1</sub>В<sub>2</sub>В<sub>3</sub> равны по первому признаку. У них А<sub>1</sub>А<sub>2</sub>=В<sub>1</sub>В<sub>2</sub>, А2Аз = В2Вл и [[Image:20-06-61.jpg]]А<sub>1</sub>А<sub>2</sub>А<sub>3</sub>= [[Image:20-06-61.jpg]]В<sub>1</sub>В<sub>2</sub>В<sub>3</sub>. | + | [[Треугольник. Полные уроки|Треугольники]] А<sub>1</sub>А<sub>2</sub>А<sub>3</sub> и В<sub>1</sub>В<sub>2</sub>В<sub>3</sub> равны по первому признаку. У них А<sub>1</sub>А<sub>2</sub>=В<sub>1</sub>В<sub>2</sub>, А2Аз = В2Вл и [[Image:20-06-61.jpg]]А<sub>1</sub>А<sub>2</sub>А<sub>3</sub>= [[Image:20-06-61.jpg]]В<sub>1</sub>В<sub>2</sub>В<sub>3</sub>.<br> <br>[[Image:24-06-87.jpg|480px|Подобие правильных выпуклых многоугольников]]<br><br><br>Подвергнем [[Площадь ортогональной проекции многоугольника|многоугольник]] P<sub>1</sub> движению, при котором его вершины А<sub>1</sub>А<sub>2</sub>А<sub>3</sub> переходят в вершины В<sub>1</sub>В<sub>2</sub>В<sub>3</sub> соответственно. Как мы знаем, такое движение существует. При этом вершина А<sub>4</sub> перейдет в некоторую точку С. Точки В<sub>4</sub> иС лежат по одну сторону с точкой В<sub>1</sub> относительно прямой В<sub>2</sub>В<sub>3</sub>. Так как движение сохраняет углы и расстояния, то [[Image:20-06-61.jpg]]В<sub>2</sub>В<sub>3</sub>С= [[Image:20-06-61.jpg]]В<sub>2</sub>В<sub>3</sub>В<sub>4</sub> и В<sub>З</sub>С=В<sub>З</sub>В<sub>4</sub>- А значит, точка С совпадает с точкой В<sub>4</sub>. Итак, при нашем движении вершина А4<sub></sub> переходит в вершину В<sub>4</sub>. Далее таким же способом заключаем, что вершина переходит в вершину В<sub>5</sub> и т. д. То есть многоугольник Р<sub>1</sub> переводится движением в многоугольник Р<sub>2</sub>, а значит, они равны.<br> |
| | | | |
| - | <br> <br>[[Image:24-06-87.jpg]]<br><br><br>Подвергнем многоугольник P<sub>1</sub> движению, при котором его вершины А<sub>1</sub>А<sub>2</sub>А<sub>3</sub> переходят в вершины В<sub>1</sub>В<sub>2</sub>В<sub>3</sub> соответственно. Как мы знаем, такое движение существует. При этом вершина А<sub>4</sub> перейдет в некоторую точку С. Точки В<sub>4</sub> иС лежат по одну сторону с точкой В<sub>1</sub> относительно прямой В<sub>2</sub>В<sub>3</sub>. Так как движение сохраняет углы и расстояния, то [[Image:20-06-61.jpg]]В<sub>2</sub>В<sub>3</sub>С= [[Image:20-06-61.jpg]]В<sub>2</sub>В<sub>3</sub>В<sub>4</sub> и В<sub>З</sub>С=В<sub>З</sub>В<sub>4</sub>- А значит, точка С совпадает с точкой В<sub>4</sub>. Итак, при нашем движении вершина А4<sub></sub> переходит в вершину В<sub>4</sub>. Далее таким же способом заключаем, что вершина переходит в вершину В<sub>5</sub> и т. д. То есть многоугольник Р<sub>1</sub> переводится движением в многоугольник Р<sub>2</sub>, а значит, они равны.<br>
| + | Чтобы доказать первое утверждение теоремы, подвергнем сначала многоугольник P<sub>1</sub> [[Преобразование подобия|преобразованию подобия]], например в гомотетии, с коэффициентом подобия [[Image:24-06-88.jpg|Формула]]-. При этом получим правильный n-угольник Р' с такими же сторонами, как и у Р<sub>2</sub>. |
| | | | |
| - | Чтобы доказать первое утверждение теоремы, подвергнем сначала многоугольник P<sub>1</sub> преобразованию подобия, например в гомотетии, с коэффициентом подобия [[Image:24-06-88.jpg]]-. При этом получим правильный n-угольник Р' с такими же сторонами, как и у Р<sub>2</sub>.
| + | По доказанному многоугольник Р' переводится движением в многоугольник P<sub>2</sub>, а значит, многоугольник Р<sub>1</sub> переводится в многоугольник Р<sub>2</sub> преобразованием подобия и движением. А это есть снова преобразование подобия. Теорема доказана. |
| | | | |
| - | По доказанному многоугольник Р' переводится движением в многоугольник P<sub>2</sub>, а значит, многоугольник Р<sub>1</sub> переводится в многоугольник Р<sub>2</sub> преобразованием подобия и движением. А это есть снова преобразование подобия. Теорема доказана.
| + | У подобных фигур [[Задачі: Переставна і сполучна властивості множення. Коефіцієнт|коэффициент]] подобия равен отношению соответствующих линейных размеров. У правильных n-угольников такими линейными размерами являются длины сторон, радиусы вписанных и описанных окружностей. Отсюда следует, что у правильных n-угольников отношения сторон, радиусов вписанных и радиусов описанных окружностей равны. А так как периметры n-угольников тоже относятся как стороны, то у правильных n-угольников отношения периметров, радиусов вписанных и радиусов описанных окружностей равны. |
| | + | |
| | + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | У подобных фигур коэффициент подобия равен отношению соответствующих линейных размеров. У правильных n-угольников такими линейными размерами являются длины сторон, радиусы вписанных и описанных окружностей. Отсюда следует, что у правильных n-угольников отношения сторон, радиусов вписанных и радиусов описанных окружностей равны. А так как периметры n-угольников тоже относятся как стороны, то у правильных n-угольников отношения периметров, радиусов вписанных и радиусов описанных окружностей равны.<br><br>
| |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Планирование по математике , учебники и книги [[Гипермаркет знаний - первый в мире!|онлайн]], курсы и задачи по математике для 9 класса [[Математика|скачать]]</sub> <br> | | <sub>Планирование по математике , учебники и книги [[Гипермаркет знаний - первый в мире!|онлайн]], курсы и задачи по математике для 9 класса [[Математика|скачать]]</sub> <br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 12:03, 11 октября 2012
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика:Подобие правильных выпуклых многоугольников
Подобие правильных выпуклых многоугольников
Теорема 13.4. Правильные выпуклые n-угольники подобны. В частности, если у них стороны одинаковы, то они равны.
Доказательство. Докажем сначала второе утверждение теоремы. Итак, пусть Р1: А1А2...Аn, P2: B1B2...Bn — правильные выпуклые n-угольники с одинаковыми сторонами (рис. 287). Докажем, что они равны, т. е. совмещаются движением.
Треугольники А1А2А3 и В1В2В3 равны по первому признаку. У них А1А2=В1В2, А2Аз = В2Вл и  А1А2А3= А1А2А3=  В1В2В3. В1В2В3.
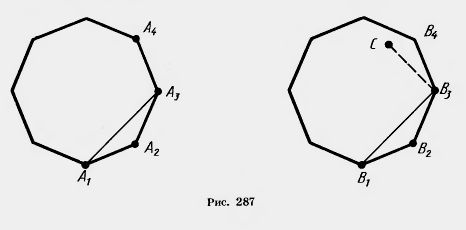
Подвергнем многоугольник P1 движению, при котором его вершины А1А2А3 переходят в вершины В1В2В3 соответственно. Как мы знаем, такое движение существует. При этом вершина А4 перейдет в некоторую точку С. Точки В4 иС лежат по одну сторону с точкой В1 относительно прямой В2В3. Так как движение сохраняет углы и расстояния, то  В2В3С= В2В3С=  В2В3В4 и ВЗС=ВЗВ4- А значит, точка С совпадает с точкой В4. Итак, при нашем движении вершина А4 переходит в вершину В4. Далее таким же способом заключаем, что вершина переходит в вершину В5 и т. д. То есть многоугольник Р1 переводится движением в многоугольник Р2, а значит, они равны. В2В3В4 и ВЗС=ВЗВ4- А значит, точка С совпадает с точкой В4. Итак, при нашем движении вершина А4 переходит в вершину В4. Далее таким же способом заключаем, что вершина переходит в вершину В5 и т. д. То есть многоугольник Р1 переводится движением в многоугольник Р2, а значит, они равны.
Чтобы доказать первое утверждение теоремы, подвергнем сначала многоугольник P1 преобразованию подобия, например в гомотетии, с коэффициентом подобия 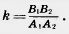 -. При этом получим правильный n-угольник Р' с такими же сторонами, как и у Р2. -. При этом получим правильный n-угольник Р' с такими же сторонами, как и у Р2.
По доказанному многоугольник Р' переводится движением в многоугольник P2, а значит, многоугольник Р1 переводится в многоугольник Р2 преобразованием подобия и движением. А это есть снова преобразование подобия. Теорема доказана.
У подобных фигур коэффициент подобия равен отношению соответствующих линейных размеров. У правильных n-угольников такими линейными размерами являются длины сторон, радиусы вписанных и описанных окружностей. Отсюда следует, что у правильных n-угольников отношения сторон, радиусов вписанных и радиусов описанных окружностей равны. А так как периметры n-угольников тоже относятся как стороны, то у правильных n-угольников отношения периметров, радиусов вписанных и радиусов описанных окружностей равны.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Планирование по математике , учебники и книги онлайн, курсы и задачи по математике для 9 класса скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|











