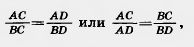|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Геометрия, урок, на Тему, Подобие прямоугольных треугольников</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Геометрия, урок, на Тему, Подобие прямоугольных треугольников, треугольника, пропорциональность, углы, биссектрисы, отрезки</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Подобие прямоугольных треугольников''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Подобие прямоугольных треугольников''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' ПОДОБИЕ ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ''' | + | '''Подобие прямоугольных треугольников''' |
| | | | |
| - | <br>У прямоугольного треугольника один угол прямой. Поэтому по теореме 11.2 '''''для подобия двух прямоугольных треугольников достаточно, чтобы у них было по равному острому углу.''''' | + | <br>У прямоугольного [[Презентація уроку на тему «Трикутник і його елементи»|треугольника]] один угол прямой. Поэтому по теореме 11.2 для подобия двух прямоугольных треугольников достаточно, чтобы у них было по равному острому углу. |
| | | | |
| - | С помощью этого признака подобия прямоугольных треугольников докажем некоторые соотношения в треугольниках. | + | С помощью этого признака подобия прямоугольных треугольников докажем некоторые соотношения в треугольниках. |
| | | | |
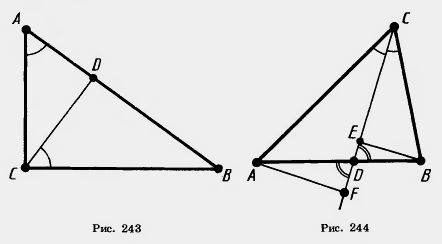
| - | Пусть ABC — прямоугольный треугольник с прямым углом С. Проведем высоту CD из вершины прямого угла (рис. 243). | + | Пусть ABC — прямоугольный треугольник с прямым углом С. Проведем высоту CD из вершины прямого угла (рис. 243). |
| | | | |
| - | Треугольники ABC и CBD имеют обпщй угол при вершине В. Следовательно, они подобны: [[Image:21-06-11.jpg]]АВС[[Image:24-06-6.jpg]][[Image:21-06-11.jpg]]CBD. Из подобия треугольников следует пропорциональность соответствующих сторон: | + | Треугольники ABC и CBD имеют обпщй угол при вершине В. Следовательно, они подобны: [[Image:21-06-11.jpg]]АВС[[Image:24-06-6.jpg]][[Image:21-06-11.jpg]]CBD. Из подобия треугольников следует [[Пряма пропорційна залежність|пропорциональность]] соответствующих сторон: |
| | | | |
| - | [[Image:24-06-16.jpg]]<br><br>Это соотношение обычно формулируют так: '''''катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.''''' | + | [[Image:24-06-16.jpg|240px|Подобие прямоугольных треугольников]]<br><br>Это соотношение обычно формулируют так: катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу. |
| | | | |
| - | Прямоугольные треугольники ACD и CBD также подобны. У них равны острые углы при вершинах А и С. Из подобия этих треугольников следует пропорциональность их сторон: | + | Прямоугольные треугольники ACD и CBD также подобны. У них равны острые [[Построение угла, равного данному. Полные уроки|углы]] при вершинах А и С. Из подобия этих треугольников следует пропорциональность их сторон: |
| | | | |
| - | [[Image:24-06-17.jpg]]<br><br>Это соотношение обычно формулируют так: '''''высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу.''''' | + | [[Image:24-06-17.jpg|240px|Подобие прямоугольных треугольников]]<br><br>Это соотношение обычно формулируют так: высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу. |
| | | | |
| - | ''
| |
| | | | |
| - | [[Image:24-06-18.jpg]]<br> <br>Докажем следующее свойство биссектрисы треугольника: '''''биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам.'''''
| |
| | | | |
| - | Пусть CD — биссектриса треугольника ABC (рис. 244). Если треугольник ABC равнобедренный с основанием АВ, то указанное свойство биссектрисы очевидно, так как в этом случае биссектриса CD является и медианой.
| + | [[Image:24-06-18.jpg|480px|Подобие прямоугольных треугольников]]<br> <br>Докажем следующее свойство [[Построение биссектрисы угла. Полные уроки|биссектрисы]] треугольника: биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам. |
| | | | |
| - | Рассмотрим общий случай, когда АС[[Image:21-06-9.jpg]]ВС. Опустим перпендикуляры AF и BE из вершин А и В на прямую CD.
| + | Пусть CD — биссектриса треугольника ABC (рис. 244). Если треугольник ABC равнобедренный с основанием АВ, то указанное свойство биссектрисы очевидно, так как в этом случае биссектриса CD является и медианой. |
| | | | |
| - | Прямоугольные треугольники АСЕ и ВСЕ подобны, так как у них равны острые углы при вершине С. Из подобия треугольников следует пропорциональность сторон:
| + | Рассмотрим общий случай, когда АС[[Image:21-06-9.jpg]]ВС. Опустим перпендикуляры AF и BE из вершин А и В на прямую CD. |
| | | | |
| - | [[Image:24-06-19.jpg]]<br><br>Прямоугольные треугольники ADF и BDE тоже подобны. У них углы при вершине D равны как вертикальные. Из подобия треугольников следует пропорциональность сторон:
| + | Прямоугольные треугольники АСЕ и ВСЕ подобны, так как у них равны острые углы при вершине С. Из подобия треугольников следует пропорциональность сторон: |
| | | | |
| - | [[Image:24-06-20.jpg]]<br><br>Сравнивая это равенство с предыдущим, получим: | + | [[Image:24-06-19.jpg|80px|Формула]]<br>Прямоугольные треугольники ADF и BDE тоже подобны. У них углы при вершине D равны как вертикальные. Из подобия треугольников следует пропорциональность сторон: |
| | + | |
| | + | [[Image:24-06-20.jpg|80px|Формула]]<br>Сравнивая это равенство с предыдущим, получим: |
| | + | |
| | + | [[Image:24-06-21.jpg|240px|Формула]]<br> <br>Т. е. [[Измерение отрезков. Полные уроки|отрезки]] AD и BD пропорциональны сторонам АС и ВС, что и требовалось доказать. |
| | + | |
| | + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | [[Image:24-06-21.jpg]]<br> <br>Т. е. отрезки AD и BD пропорциональны сторонам АС и ВС, что и требовалось доказать.<br><br>
| |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Календарно-тематическое планирование по математике, видео по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub> | | <sub>Календарно-тематическое планирование по математике, видео по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub> |
| Строка 44: |
Строка 46: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
С помощью этого признака подобия прямоугольных треугольников докажем некоторые соотношения в треугольниках.
Пусть ABC — прямоугольный треугольник с прямым углом С. Проведем высоту CD из вершины прямого угла (рис. 243).
Треугольники ABC и CBD имеют обпщй угол при вершине В. Следовательно, они подобны:  АВС
АВС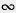
 CBD. Из подобия треугольников следует пропорциональность соответствующих сторон:
CBD. Из подобия треугольников следует пропорциональность соответствующих сторон:
Пусть CD — биссектриса треугольника ABC (рис. 244). Если треугольник ABC равнобедренный с основанием АВ, то указанное свойство биссектрисы очевидно, так как в этом случае биссектриса CD является и медианой.
Прямоугольные треугольники АСЕ и ВСЕ подобны, так как у них равны острые углы при вершине С. Из подобия треугольников следует пропорциональность сторон:
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.