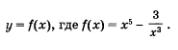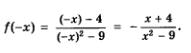|
|
|
| Строка 1: |
Строка 1: |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Четные и нечетные функции<metakeywords>Четные и нечетные функции</metakeywords>''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Четные и нечетные функции<metakeywords>Четные и нечетные функции</metakeywords>''' |
| | | | |
| | + | <br> |
| | | | |
| | + | '''ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ'''<br>В предыдущем параграфе мы обсуждали только те свойства функций, которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе.<br>'''Определение 1.''' Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).<br>'''Определение 2.''' Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).<br>'''Пример 1.''' Доказать, что у = х<sup>4</sup> — четная функция.<br>'''Решение.''' Имеем: f(х) = х<sup>4</sup>, f(-х) = (-х)<sup>4</sup>. Но (-х)<sup>4</sup> = х<sup>4</sup>. Значит, для любого х выполняется равенство f(-х) = f(х), т.е. функция является четной. <br>Аналогично можно доказать, что функции у — х<sup>2</sup>,у = х<sup>6</sup>,у — х<sup>8</sup> являются четными.<br>'''Пример 2. '''Доказать, что у = х<sup>3</sup>~ нечетная функция.<br>'''Решение.''' Имеем: f(х) = х<sup>3</sup>, f(-х) = (-х)<sup>3</sup>. Но (-х)<sup>3</sup> = -х<sup>3</sup>. Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной. <br>Аналогично можно доказать, что функции у = х, у = х<sup>5</sup>, у = х<sup>7</sup> являются нечетными.<br>Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х<sup>3</sup>, у = х<sup>5</sup>, у = х<sup>7</sup> — нечетные функции, тогда как у = х<sup>2</sup>, у = х<sup>4</sup>, у = х<sup>6</sup> — четные функции. И вообще для любой функции вида у = х" (ниже мы специально займемся изучением этих функций), где n — натуральное число, можно сделать вывод: если n — нечетное число, то функция у = х" — нечетная; если же n — четное число, то функция у = хn — четная.<br>Существуют и функции, не являющиеся ни четными, ни нечетными. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь [[Image:Al9111.jpg]] Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).<br>Итак, функция может быть четной, нечетной, а также ни той ни другой.<br>Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность.<br>В определениях 1 и 2 речь идет о значениях функции в точках х и -х. Тем самым предполагается, что функция определена и в точке х, и в точке -х. Это значит, что точка -х принадлежит области определения функции одновременно с точкой х. Если числовое множество X вместе с каждым своим элементом х содержит и противоположный элемент -х, то X называют симметричным множеством. Скажем, (-2, 2), [-5, 5], (-оо, +оо) — симметричные множества, в то время как [0, +оо), (-2, 3), [-5, 5) — несимметричные множества. Если функция у = f (х) — четная или нечетная, то ее область определения D (f) — симметричное множество. Если же D (f) — несимметричное множество, то функция у = f(х) не является ни четной, ни нечетной.<br>Учитывая сказанное, рекомендуем при исследовании функции на четность использовать следующий алгоритм.<br>'''Алгоритм исследования функции у = f(х) на четность'''<br>1. Установить, симметрична ли область определения функции. Если нет, то объявить, что функция не является ни четной, ни нечетной. Если да, то переходить ко второму шагу алгоритма.<br>2. Найти f(-х).<br>3. Сравнить f (x)= f (-x)<br>а) если f(-х) = f(х), то функция — четная,<br>б) если f(-х) = -f(х), то функция — нечетная;<br>в) если хотя бы в одной точке х є Х выполняется соотношение f(-х) = f(х) и хотя бы в одной точке х є X выполняется соотношение f(-х) = -f(х), то функция не является ни четной, ни нечетной.<br>'''Пример 3.''' Исследовать на четность функцию: |
| | | | |
| - | '''ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ'''<br>В предыдущем параграфе мы обсуждали только те свойства функций, которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе.<br>'''Определение 1.''' Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).<br>'''Определение 2.''' Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).<br>'''Пример 1.''' Доказать, что у = х<sup>4</sup> — четная функция.<br>'''Решение.''' Имеем: f(х) = х<sup>4</sup>, f(-х) = (-х)<sup>4</sup>. Но (-х)<sup>4</sup> = х<sup>4</sup>. Значит, для любого х выполняется равенство f(-х) = f(х), т.е. функция является четной. <br>Аналогично можно доказать, что функции у — х<sup>2</sup>,у = х<sup>6</sup>,у — х<sup>8</sup> являются четными.<br>'''Пример 2. '''Доказать, что у = х<sup>3</sup>~ нечетная функция.<br>'''Решение.''' Имеем: f(х) = х<sup>3</sup>, f(-х) = (-х)<sup>3</sup>. Но (-х)<sup>3</sup> = -х<sup>3</sup>. Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной. <br>Аналогично можно доказать, что функции у = х, у = х<sup>5</sup>, у = х<sup>7</sup> являются нечетными.<br>Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х<sup>3</sup>, у = х<sup>5</sup>, у = х<sup>7</sup> — нечетные функции, тогда как у = х<sup>2</sup>, у = х<sup>4</sup>, у = х<sup>6</sup> — четные функции. И вообще для любой функции вида у = х" (ниже мы специально займемся изучением этих функций), где n — натуральное число, можно сделать вывод: если n — нечетное число, то функция у = х" — нечетная; если же n — четное число, то функция у = хn — четная.<br>Существуют и функции, не являющиеся ни четными, ни нечетными. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь [[Image:al9111.jpg]] Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).<br>Итак, функция может быть четной, нечетной, а также ни той ни другой.<br>Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность.<br>В определениях 1 и 2 речь идет о значениях функции в точках х и -х. Тем самым предполагается, что функция определена и в точке х, и в точке -х. Это значит, что точка -х принадлежит области определения функции одновременно с точкой х. Если числовое множество X вместе с каждым своим элементом х содержит и противоположный элемент -х, то X называют симметричным множеством. Скажем, (-2, 2), [-5, 5], (-оо, +оо) — симметричные множества, в то время как [0, +оо), (-2, 3), [-5, 5) — несимметричные множества. Если функция у = f (х) — четная или нечетная, то ее область определения D (f) — симметричное множество. Если же D (f) — несимметричное множество, то функция у = f(х) не является ни четной, ни нечетной.<br>Учитывая сказанное, рекомендуем при исследовании функции на четность использовать следующий алгоритм.<br>'''Алгоритм исследования функции у = f(х) на четность'''<br>1. Установить, симметрична ли область определения функции. Если нет, то объявить, что функция не является ни четной, ни нечетной. Если да, то переходить ко второму шагу алгоритма.<br>2. Найти f(-х).<br>3. Сравнить f (x)= f (-x)<br>а) если f(-х) = f(х), то функция — четная,<br>б) если f(-х) = -f(х), то функция — нечетная;<br>в) если хотя бы в одной точке х є Х выполняется соотношение f(-х) = f(х) и хотя бы в одной точке х є X выполняется соотношение f(-х) = -f(х), то функция не является ни четной, ни нечетной.<br>'''Пример 3.''' Исследовать на четность функцию:<br>а) У = 4 + —;<br>х6<br>в) У<br>х - 4<br>б)у = х ;<br>г) у = Т^з.<br>Решение, а) у = /(ж), где /(ж) = ж4 + — .<br>1) Функция определена при всех значениях х, кроме х = 0. Следовательно, /)(/) — симметричное множество.<br>2) /(-*) = (-*)4 +<br>:х4 +<br>(-х)6 " ■ X°<br>3) Замечаем, что для любого ж из области определения функции выполняется равенство /(-*) = /(*).<br>2<br>Таким образом, у- х4+ ~ — четная функция.<br>б) У = Кх), где Кх) = - .<br>1) Функция определена при всех значениях х, кроме х = 0. Следовательно, Х>(/) — симметричное множество.<br>2 )/(-*) = (-х)5<br>= -х5 +<br>х3<br>(-ж)3 х"<br>3) Замечаем, что для любого х из области определения функции выполняется равенство К-х) = -Кх).<br>Таким образом, у = хъ- —<br>х3<br>нечетная функция.<br>в) У = Кх), где Кх) ■■<br>х-4 х2 -9'<br>1) Функция определена во всех точках х, кроме тех, которые обращают знаменатель дроби в нуль. Из условия х2 - 9 = 0 находим х = ± 3. Значит, область определения функции — числовая прямая, из которой удалены две точки: 3 и -3. Это — симметричное множество.<br>90<br>3.12. ||<br>ЧИСЛОВЫЕ ФУНКЦИИ<br>. _ (-*) - 4 х + 4<br>2) х> ~ (_л)2_9 - х2_9-<br>3) Сравнив /(-х) и /(х), замечаем, что, скорее всего, не выполняются ни тождество /(-х) = /(х), ни тождество /(-х) = -/(х). Чтобы в этом убедиться, возьмем конкретное значение х, например х = 4. Имеем: /(4) = О, а /(-4) * 0. Замечаем, что /(-4) ф /(4) и /(-4) ф -/(4).<br>Таким образом, функция не является ни четной, ни нечетной.<br>г) Функция у = - 3 определена при условии х - 3 > 0, т.е. на луче [3, +оо). Этот луч — несимметричное множество, значит, функция не является ни четной, ни нечетной. (И<br>Пример 4. Исследовать на четность функцию:<br>а)у=\х\, хе[-2, 2]; б) у = \х \, ж е [-3, 3);<br>в)у = х3, хе(-5,5); г)у = х3, хе(-5,5].<br>Решение. а)Х>(/) = [-2,21 — симметричное множество, и для всех х выполняется равенство | -х | = | х |. Значит, заданная функция — четная.<br>б) Х>(/) = [-3, 3) — несимметричное множество. В самом деле, точка -3 принадлежит полуинтервалу [-3, 3), а противоположная точка 3 не принадлежит этому полуинтервалу. Значит, функция не является ни четной, ни нечетной.
| + | [[Image:al9112.jpg]]<br>'''Решение'''<span style="font-weight: bold;">:</span>'''<span style="font-weight: bold;" /> а)''' у = f(x), где [[Image:al9113.jpg]]<br>1) Функция определена при всех значениях х, кроме х = 0. Следовательно,D (f) — симметричное множество.<br>2) [[Image:al9114.jpg]]<br>3) Замечаем, что для любого ж из области определения функции выполняется равенство f(x) = f(x).<br>Таким образом, [[Image:al9115.jpg]] четная функция.<br>'''б)''' [[Image:al9116.jpg]]<br>1) Функция определена при всех значениях х, кроме х = 0. Следовательно, D(f) — симметричное множество.<br>2 )[[Image:al9117.jpg]]<br>3) Замечаем, что для любого х из области определения функции выполняется равенство f(-х) = -f(х).<br>Таким образом, [[Image:al9118.jpg]]<br>'''в)''' [[Image:al9119.jpg]]<br>1) Функция определена во всех точках х, кроме тех, которые обращают знаменатель дроби в нуль. Из условия х<sup>2</sup> - 9 = 0 находим х = ± 3. Значит, область определения функции — числовая прямая, из которой удалены две точки: 3 и -3. Это — симметричное множество.<br>2) [[Image:al91110.jpg]]<br>3) Сравнив f(-х) и f(х), замечаем, что, скорее всего, не выполняются ни тождество f(-х) = f(х), ни тождество f(-х) = -f(х). Чтобы в этом убедиться, возьмем конкретное значение х, например х = 4. Имеем: f(4) = О, а [[Image:al91111.jpg]] Таким образом, функция не является ни четной, ни нечетной.<br>'''г)''' Функция [[Image:al91112.jpg]] определена при условии [[Image:al91113.jpg]] т.е. на луче [3, +оо). Этот луч — несимметричное множество, значит, функция не является ни четной, ни нечетной. <br>'''Пример 4.''' Исследовать на четность функцию:<br>[[Image:al91114.jpg]]<br>'''Решение.''' '''а)''' D(f) = [-2,2) — симметричное множество, и для всех х выполняется равенство | -х | = | х |. Значит, заданная функция — четная.<br>'''б) ''' D(f) = [-3, 3) — несимметричное множество. В самом деле, точка -3 принадлежит полуинтервалу [-3, 3), а противоположная точка 3 не принадлежит этому полуинтервалу. Значит, функция не является ни четной, ни нечетной. |
| | | | |
| - | в) В{Г) = (-5, 5) — симметричное множество и (-ж)3 = -ж3 для всех х из интервала (-5, 5). Значит, заданная функция — нечетная.<br>г) Функция задана на полуинтервале, который не является симметричным множеством. Значит, функция — ни четная, ни нечетная. (И<br>Теперь обсудим геометрический смысл свойства четности и свойства нечетности функции.<br>Пусть у = /(ж) — четная функция, т.е. /(-*) = /(х) для любого х е . Рассмотрим две точки графика функции: А(х; /(х)) и В(-х; /(-х)). Так как /(-х) = /(х), то у точек А и В абсциссы являются противоположными числами, а ординаты одинаковы. Эти точки симметричны относительно оси у (рис. 73). Таким образом, для каждой точки А графика четной функции у = /(х) существует<br>91<br>310-1|<br>ЧИСЛОВЫЕ ФУНКЦИИ<br>симметричная ей относительно оси у точка В того же графика. Это означает, что график четной функции симметричен относительно оси у.<br>Пусть у = Дх) — нечетная функция, т.е. Д-х) = -Дх) для любого хе !)(/). Рассмотрим две точки графика функции: А(х; Дх)) и В(-х; Д-х)). Так как Д-х) = -Дх), то у точек А и В абсциссы являются противоположными числами и ординаты являются противоположными числами. Эти точки симметричны относительно начала координат (рис. 74). Таким образом, для каждой точки А графика нечетной функции у = Дх) существует симметричная ей относительно начала координат точка В того же графика. Это означает, что график нечетной функции симметричен относительно начала координат.<br> У' к ))<br> В А <br> <br> <br> X<br> -х 0 X <br> У' к ((X) А <br> у <br> -X * * * X<br> * * 0 X <br> В' ф <br>( -х; д- <br>Рис. 73<br>Рис. 74<br>Верны и обратные утверждения:<br>1) Если график функции у = [(х) симметричен относительно оси ординат, то у = {(х) — четная функция.<br>В самом деле, симметрия графика функции у = Дх) относительно оси у означает, что для всех х из области определения функции справедливо равенство Д-х) = Дх), т.е. у = Дх) — четная функция.<br>2) Если график функции у = [(х) симметричен относительно начала координат, то у = {(х) — нечетная функция.<br>Симметрия графика функции у = Дх) относительно начала координат означает, что для всех х из области определения функции справедливо равенство Д-х) = -Дх), т.е. у — Дх) — нечетная функция.<br>92<br>3.12. ||<br>ЧИСЛОВЫЕ ФУНКЦИИ<br>Пример 5. Исследовать на четность функцию<br>У = 49-х2 .<br>Решение. Первый способ. Имеем<br>/(ж) = 49-х2; /(-ж) = л/9 - (-х)2 = 49-х2 . Значит, для любого х из Х)(/) справедливо равенство Д-х) = Дх), т.е. функция является четной.<br>Второй способ. Графиком функции служит полуокружность с центром в начале координат и радиусом 3 (см. рис.52 из § 9), она симметрична относительно оси у. Это означает, что<br>у = 49 - X2 — четная функция. <И | + | '''в)''' D (f) = (-5, 5) — симметричное множество и (-x)<sup>3</sup> = -ж<sup>3</sup> для всех х из интервала (-5, 5). Значит, заданная функция — нечетная.<br>'''г)''' Функция задана на полуинтервале, который не является симметричным множеством. Значит, функция — ни четная, ни нечетная. <br>Теперь обсудим геометрический смысл свойства четности и свойства нечетности функции.<br>Пусть у = f(x) — четная функция, т.е. f(x) = f(х) для любого х е . Рассмотрим две точки графика функции: D(х; f(х)) и В(-х; f(-х)). Так как f(-х) = f(х), то у точек А и В абсциссы являются противоположными числами, а ординаты одинаковы. Эти точки симметричны относительно оси у (рис. 73). Таким образом, для каждой точки А графика четной функции у = f(х) существует симметричная ей относительно оси у точка В того же графика. Это означает, что график четной функции симметричен относительно оси у.<br>Пусть у = Дх) — нечетная функция, т.е. Д-х) = -Дх) для любого хе !)(/). Рассмотрим две точки графика функции: А(х; Дх)) и В(-х; Д-х)). Так как Д-х) = -Дх), то у точек А и В абсциссы являются противоположными числами и ординаты являются противоположными числами. Эти точки симметричны относительно начала координат (рис. 74). Таким образом, для каждой точки А графика нечетной функции у = Дх) существует симметричная ей относительно начала координат точка В того же графика. Это означает, что график нечетной функции симметричен относительно начала координат.<br> У' к ))<br> В А <br> <br> <br> X<br> -х 0 X <br> У' к ((X) А <br> у <br> -X * * * X<br> * * 0 X <br> В' ф <br>( -х; д- <br>Рис. 73<br>Рис. 74<br>Верны и обратные утверждения:<br>1) Если график функции у = [(х) симметричен относительно оси ординат, то у = {(х) — четная функция.<br>В самом деле, симметрия графика функции у = Дх) относительно оси у означает, что для всех х из области определения функции справедливо равенство Д-х) = Дх), т.е. у = Дх) — четная функция.<br>2) Если график функции у = [(х) симметричен относительно начала координат, то у = {(х) — нечетная функция.<br>Симметрия графика функции у = Дх) относительно начала координат означает, что для всех х из области определения функции справедливо равенство Д-х) = -Дх), т.е. у — Дх) — нечетная функция.<br>92<br>3.12. ||<br>ЧИСЛОВЫЕ ФУНКЦИИ<br>Пример 5. Исследовать на четность функцию<br>У = 49-х2 .<br>Решение. Первый способ. Имеем<br>/(ж) = 49-х2; /(-ж) = л/9 - (-х)2 = 49-х2 . Значит, для любого х из Х)(/) справедливо равенство Д-х) = Дх), т.е. функция является четной.<br>Второй способ. Графиком функции служит полуокружность с центром в начале координат и радиусом 3 (см. рис.52 из § 9), она симметрична относительно оси у. Это означает, что<br>у = 49 - X2 — четная функция. <И |
| | | | |
| | А.Г. Мордкович Алгебра 9 класс | | А.Г. Мордкович Алгебра 9 класс |
Версия 08:37, 30 июня 2010
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Четные и нечетные функции
ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ
В предыдущем параграфе мы обсуждали только те свойства функций, которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе.
Определение 1. Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).
Определение 2. Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).
Пример 1. Доказать, что у = х4 — четная функция.
Решение. Имеем: f(х) = х4, f(-х) = (-х)4. Но (-х)4 = х4. Значит, для любого х выполняется равенство f(-х) = f(х), т.е. функция является четной.
Аналогично можно доказать, что функции у — х2,у = х6,у — х8 являются четными.
Пример 2. Доказать, что у = х3~ нечетная функция.
Решение. Имеем: f(х) = х3, f(-х) = (-х)3. Но (-х)3 = -х3. Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной.
Аналогично можно доказать, что функции у = х, у = х5, у = х7 являются нечетными.
Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х3, у = х5, у = х7 — нечетные функции, тогда как у = х2, у = х4, у = х6 — четные функции. И вообще для любой функции вида у = х" (ниже мы специально займемся изучением этих функций), где n — натуральное число, можно сделать вывод: если n — нечетное число, то функция у = х" — нечетная; если же n — четное число, то функция у = хn — четная.
Существуют и функции, не являющиеся ни четными, ни нечетными. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь 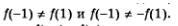 Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х). Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).
Итак, функция может быть четной, нечетной, а также ни той ни другой.
Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность.
В определениях 1 и 2 речь идет о значениях функции в точках х и -х. Тем самым предполагается, что функция определена и в точке х, и в точке -х. Это значит, что точка -х принадлежит области определения функции одновременно с точкой х. Если числовое множество X вместе с каждым своим элементом х содержит и противоположный элемент -х, то X называют симметричным множеством. Скажем, (-2, 2), [-5, 5], (-оо, +оо) — симметричные множества, в то время как [0, +оо), (-2, 3), [-5, 5) — несимметричные множества. Если функция у = f (х) — четная или нечетная, то ее область определения D (f) — симметричное множество. Если же D (f) — несимметричное множество, то функция у = f(х) не является ни четной, ни нечетной.
Учитывая сказанное, рекомендуем при исследовании функции на четность использовать следующий алгоритм.
Алгоритм исследования функции у = f(х) на четность
1. Установить, симметрична ли область определения функции. Если нет, то объявить, что функция не является ни четной, ни нечетной. Если да, то переходить ко второму шагу алгоритма.
2. Найти f(-х).
3. Сравнить f (x)= f (-x)
а) если f(-х) = f(х), то функция — четная,
б) если f(-х) = -f(х), то функция — нечетная;
в) если хотя бы в одной точке х є Х выполняется соотношение f(-х) = f(х) и хотя бы в одной точке х є X выполняется соотношение f(-х) = -f(х), то функция не является ни четной, ни нечетной.
Пример 3. Исследовать на четность функцию:

Решение:<span style="font-weight: bold;" /> а) у = f(x), где 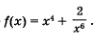
1) Функция определена при всех значениях х, кроме х = 0. Следовательно,D (f) — симметричное множество.
2) 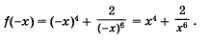
3) Замечаем, что для любого ж из области определения функции выполняется равенство f(x) = f(x).
Таким образом, 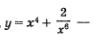 четная функция. четная функция.
б) 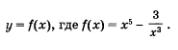
1) Функция определена при всех значениях х, кроме х = 0. Следовательно, D(f) — симметричное множество.
2 )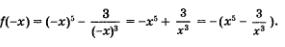
3) Замечаем, что для любого х из области определения функции выполняется равенство f(-х) = -f(х).
Таким образом, 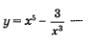
в) 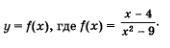
1) Функция определена во всех точках х, кроме тех, которые обращают знаменатель дроби в нуль. Из условия х2 - 9 = 0 находим х = ± 3. Значит, область определения функции — числовая прямая, из которой удалены две точки: 3 и -3. Это — симметричное множество.
2) 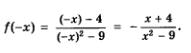
3) Сравнив f(-х) и f(х), замечаем, что, скорее всего, не выполняются ни тождество f(-х) = f(х), ни тождество f(-х) = -f(х). Чтобы в этом убедиться, возьмем конкретное значение х, например х = 4. Имеем: f(4) = О, а 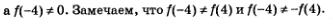 Таким образом, функция не является ни четной, ни нечетной. Таким образом, функция не является ни четной, ни нечетной.
г) Функция 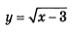 определена при условии определена при условии 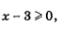 т.е. на луче [3, +оо). Этот луч — несимметричное множество, значит, функция не является ни четной, ни нечетной. т.е. на луче [3, +оо). Этот луч — несимметричное множество, значит, функция не является ни четной, ни нечетной.
Пример 4. Исследовать на четность функцию:
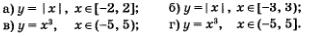
Решение. а) D(f) = [-2,2) — симметричное множество, и для всех х выполняется равенство | -х | = | х |. Значит, заданная функция — четная.
б) D(f) = [-3, 3) — несимметричное множество. В самом деле, точка -3 принадлежит полуинтервалу [-3, 3), а противоположная точка 3 не принадлежит этому полуинтервалу. Значит, функция не является ни четной, ни нечетной.
в) D (f) = (-5, 5) — симметричное множество и (-x)3 = -ж3 для всех х из интервала (-5, 5). Значит, заданная функция — нечетная.
г) Функция задана на полуинтервале, который не является симметричным множеством. Значит, функция — ни четная, ни нечетная.
Теперь обсудим геометрический смысл свойства четности и свойства нечетности функции.
Пусть у = f(x) — четная функция, т.е. f(x) = f(х) для любого х е . Рассмотрим две точки графика функции: D(х; f(х)) и В(-х; f(-х)). Так как f(-х) = f(х), то у точек А и В абсциссы являются противоположными числами, а ординаты одинаковы. Эти точки симметричны относительно оси у (рис. 73). Таким образом, для каждой точки А графика четной функции у = f(х) существует симметричная ей относительно оси у точка В того же графика. Это означает, что график четной функции симметричен относительно оси у.
Пусть у = Дх) — нечетная функция, т.е. Д-х) = -Дх) для любого хе !)(/). Рассмотрим две точки графика функции: А(х; Дх)) и В(-х; Д-х)). Так как Д-х) = -Дх), то у точек А и В абсциссы являются противоположными числами и ординаты являются противоположными числами. Эти точки симметричны относительно начала координат (рис. 74). Таким образом, для каждой точки А графика нечетной функции у = Дх) существует симметричная ей относительно начала координат точка В того же графика. Это означает, что график нечетной функции симметричен относительно начала координат.
У' к ))
В А
X
-х 0 X
У' к ((X) А
у
-X * * * X
* * 0 X
В' ф
( -х; д-
Рис. 73
Рис. 74
Верны и обратные утверждения:
1) Если график функции у = [(х) симметричен относительно оси ординат, то у = {(х) — четная функция.
В самом деле, симметрия графика функции у = Дх) относительно оси у означает, что для всех х из области определения функции справедливо равенство Д-х) = Дх), т.е. у = Дх) — четная функция.
2) Если график функции у = [(х) симметричен относительно начала координат, то у = {(х) — нечетная функция.
Симметрия графика функции у = Дх) относительно начала координат означает, что для всех х из области определения функции справедливо равенство Д-х) = -Дх), т.е. у — Дх) — нечетная функция.
92
3.12. ||
ЧИСЛОВЫЕ ФУНКЦИИ
Пример 5. Исследовать на четность функцию
У = 49-х2 .
Решение. Первый способ. Имеем
/(ж) = 49-х2; /(-ж) = л/9 - (-х)2 = 49-х2 . Значит, для любого х из Х)(/) справедливо равенство Д-х) = Дх), т.е. функция является четной.
Второй способ. Графиком функции служит полуокружность с центром в начале координат и радиусом 3 (см. рис.52 из § 9), она симметрична относительно оси у. Это означает, что
у = 49 - X2 — четная функция. <И
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|