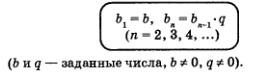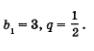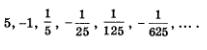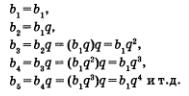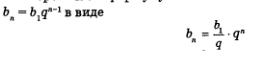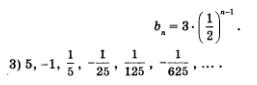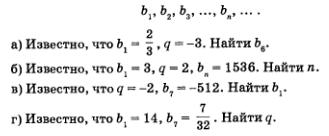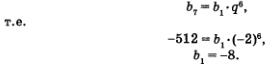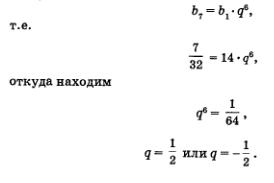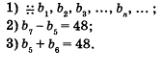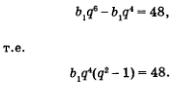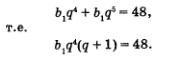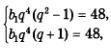|
|
|
| Строка 9: |
Строка 9: |
| | [[Image:Al91715.jpg]]<br>''Это — формула п-го члена геометрической прогрессии.''<br>'''Замечание.''' Если вы прочли важное замечание из предыдущего параграфа и поняли его, то попробуйте доказать формулу (1) методом математической индукции подобно тому, как зто было сделано для формулы п-го члена арифметической прогрессии.<br>Перепишем формулу п-го члена геометрической прогрессии | | [[Image:Al91715.jpg]]<br>''Это — формула п-го члена геометрической прогрессии.''<br>'''Замечание.''' Если вы прочли важное замечание из предыдущего параграфа и поняли его, то попробуйте доказать формулу (1) методом математической индукции подобно тому, как зто было сделано для формулы п-го члена арифметической прогрессии.<br>Перепишем формулу п-го члена геометрической прогрессии |
| | | | |
| - | [[Image:Al91716.jpg]] <br>и введем обозначения: [[Image:Al91717.jpg]] Получим у = mq<sup>2</sup>, или, подробнее, [[Image:Al91718.jpg]]<br>Аргумент х содержится в показателе степени, поэтому такую функцию называют показательной функцией. Значит, геометрическую прогрессию можно рассматривать как показательную функцию, заданную на множестве N натуральных чисел. На рис. 96а изображен график функции [[Image:al91719.jpg]] рис. 966 — график функции [[Image:al91720.jpg]] В обоих случаях имеем изолированные точки<br>(с абсциссами х= 1, х = 2, х = 3 и т.д.), лежащие на некоторой кривой (на обоих рисунках представлена одна и та же кривая, только по-разному расположенная и изображенная в разных масштабах). Эту кривую называют экспонентой. Подробнее о показательной функции и ее графике речь пойдет в курсе алгебры 11-го класса. | + | [[Image:Al91716.jpg]] <br>и введем обозначения: [[Image:Al91717.jpg]] Получим у = mq<sup>2</sup>, или, подробнее, [[Image:Al91718.jpg]]<br>Аргумент х содержится в показателе степени, поэтому такую функцию называют показательной функцией. Значит, геометрическую прогрессию можно рассматривать как показательную функцию, заданную на множестве N натуральных чисел. На рис. 96а изображен график функции [[Image:Al91719.jpg]] рис. 966 — график функции [[Image:Al91720.jpg]] В обоих случаях имеем изолированные точки<br>(с абсциссами х= 1, х = 2, х = 3 и т.д.), лежащие на некоторой кривой (на обоих рисунках представлена одна и та же кривая, только по-разному расположенная и изображенная в разных масштабах). Эту кривую называют экспонентой. Подробнее о показательной функции и ее графике речь пойдет в курсе алгебры 11-го класса. |
| | | | |
| - | [[Image:al91721.jpg]]<br> Вернемся к примерам 1—5 из предыдущего пункта. | + | [[Image:Al91721.jpg]]<br> Вернемся к примерам 1—5 из предыдущего пункта. |
| | | | |
| - | 1) 1, 3, 9, 27, 81,... . Это геометрическая прогрессия, у которой Ь<sub>1</sub> = 1, q = 3. Составим формулу п-го члена [[Image:al91722.jpg]]<br>2) [[Image:al91723.jpg]] Это геометрическая прогрессия, у которой [[Image:al91724.jpg]] Составим формулу п-го члена<br>[[Image:al91725.jpg]]<br>Это геометрическая прогрессия, у которой [[Image:al91726.jpg]] Составим формулу п-го члена [[Image:al91727.jpg]]<br>4) 8, 8, 8, ..., 8, ... . Это геометрическая прогрессия, у которой Ь<sub>1</sub> = 8, q = 1. Составим формулу п-го члена [[Image:al91728.jpg]]<br>5) 2, -2, 2, -2, 2, -2,.... Это геометрическая прогрессия, у которой Ъ<sub>1</sub> = 2, q = —1. Составим формулу п-го члена [[Image:al91729.jpg]]<br>'''Пример 6.''' Дана геометрическая прогрессия | + | 1) 1, 3, 9, 27, 81,... . Это геометрическая прогрессия, у которой Ь<sub>1</sub> = 1, q = 3. Составим формулу п-го члена [[Image:Al91722.jpg]]<br>2) [[Image:Al91723.jpg]] Это геометрическая прогрессия, у которой [[Image:Al91724.jpg]] Составим формулу п-го члена<br>[[Image:Al91725.jpg]]<br>Это геометрическая прогрессия, у которой [[Image:Al91726.jpg]] Составим формулу п-го члена [[Image:Al91727.jpg]]<br>4) 8, 8, 8, ..., 8, ... . Это геометрическая прогрессия, у которой Ь<sub>1</sub> = 8, q = 1. Составим формулу п-го члена [[Image:Al91728.jpg]]<br>5) 2, -2, 2, -2, 2, -2,.... Это геометрическая прогрессия, у которой Ъ<sub>1</sub> = 2, q = —1. Составим формулу п-го члена [[Image:Al91729.jpg]]<br>'''Пример 6.''' Дана геометрическая прогрессия |
| | | | |
| - | [[Image:al91730.jpg]]<br>'''Р е ш е н и е.''' Во всех случаях в основе решения лежит формула п-го члена геометрической прогрессии | + | [[Image:Al91730.jpg]]<br>'''Р е ш е н и е.''' Во всех случаях в основе решения лежит формула п-го члена геометрической прогрессии |
| | | | |
| - | [[Image:al91731.jpg]]<br>а) Положив в формуле п-го члена геометрической прогрессии п = 6, получим | + | [[Image:Al91731.jpg]]<br>а) Положив в формуле п-го члена геометрической прогрессии п = 6, получим |
| | | | |
| - | [[Image:al91732.jpg]]<br>б) Имеем | + | [[Image:Al91732.jpg]]<br>б) Имеем |
| | | | |
| - | [[Image:al91733.jpg]]<br>Ъп = ЪхЧ"-\<br>135<br>4.16. ||<br>ПРОГРЕССИИ<br>т.е.<br>1536 = 3-2""1, 512 = 2"1.<br>Так как 512 = 29, то получаем п - 1 = 9, п = 10. в) Имеем<br>т.е.<br>г) Имеем<br>т.е.<br>Ь^Ъ.-я6,<br>-512 = Ь1-(-2)6, Ьх = - 8.<br>Ь7 = гу</6><br>^ = 14 • д6,<br>откуда находим<br>или 1 = ®<br>Пример 7. Разность между седьмым и пятым членами геометрической прогрессии равна 48, сумма пятого и шестого членов прогрессии также равна 48. Найти двенадцатый член этой прогрессии.<br>Решение. Первый этап. Составление математической модели.<br>Условия задачи можно кратко записать так:<br>1) ЦЬ1гЬ2,Ья, ...,&„, ... ;<br>2)Ь7-Ь5 = 48;<br>3)Ь5 + Ь6 = 48.<br>Воспользовавшись формулой п-го члена геометрической прогрессии, получим:<br>Ь7 = Ь1дб. Ь5 = Ъ6 = Ь Тогда второе условие задачи (Ь7 - Ь5 = 48) можно записать в виде<br>Ь196-Ь1д4 = 48,<br>136<br>4.16. ||<br>ПРОГРЕССИИ<br>т.е.<br>б^д2- 1) = 48. Третье условие задачи (Ь5 + Ь6 = 48) можно записать в виде<br>Ъ^ + Ъхд5 = 48,<br>т.е.<br>6^ + 1) = 48.<br>В итоге получаем систему двух уравнений с двумя переменными Ьг и д:<br>кд4(?2-1) = 48, Кд4(д + 1) = 48,<br>которая в сочетании с записанным выше условием 1) и представляет собой математическую модель задачи.<br>Второй этап. Работа с составленной моделью. Приравняв левые части обоих уравнений системы, получим:<br>М4(д2-1) = 6^(9+1); д2 - 1 = д + 1<br>(мы разделили обе части уравнения на выражение Ъ^, отличное от нуля).<br>Из уравнения д2 - д - 2 = 0 находим дх = 2, д2 = -1. Подставив значение д = 2 во второе уравнение системы, получим Ъх• 16• 3 = 48, т.е. Ъх= 1.<br>Подставив значение д = -1 во второе уравнение системы, получим Ьг • 1 • 0 = 48; это уравнение не имеет решений.<br>Итак, 6=1,9 = 2 — эта пара является решением составленной системы уравнений.<br>Теперь мы можем записать геометрическую прогрессию, о которой идет речь в задаче: 1, 2, 4, 8, 16, 32, ... .<br>Третий этап. Ответ на вопрос задачи. Требуется вычислить 612. Имеем<br>612 = 61д11 = 1-211 = 2048. О т в е т: 612 = 2048.<br>137<br>4.16. ||<br>ПРОГРЕССИИ<br>3. Формула суммы членов конечной геометрической прогрессии.<br>Пусть дана конечная геометрическая прогрессия<br>Н ь1,ь2,ь3,...,ъп_2,ъп_1,ьп.<br>Обозначим через 5 сумму ее членов, т.е.<br>8п = Ь1 + Ь2 + Ъ3 +<br>+ ь. + ьп. + ь<br>П-2 Л-1 Л<br>Выведем формулу для отыскания этой суммы.<br>Начнем с самого простого случая, когда д = 1. Тогда геометрическая прогрессия Ьх, Ь2, Ь3,..., Ъп состоит из п чисел, равных Ъх, т.е. прогрессия имеет вид Ъх, Ъх, Ъх, ..., Ьх. Сумма этих чисел равна пЪх.<br>Пусть теперь д Ф 1. Для отыскания <§п применим искусственный прием: выполним некоторые преобразования выражения 8д. Имеем:<br>5 д = (Ьх + Ь2 + Ь3 + ... + Ъп 2 + Ь^ + Ьп)д = = Ьхц + Ь2д + &3д + ... + Ьп2д + Ъп_хд + Ь„д = = + + Ь. + ... + & , + Ь + Ьа =<br>2 3 4 п-1 п л*<br>4 1 2 3 п-2 п-1 п' п1 1<br>= 5 + &д-& =5 +(Ь -д^-д-Ь =5 +Ь,дп-Ь,.<br>п 1 п у 1 ^ ' * 1 п 1<br>Итак, мы доказали, что<br>5 д = 8 + 6,д" - Ь,.<br>п* п I* 1<br>(1)<br>Выполняя преобразования, мы, во-первых, пользовались определением геометрической прогрессии, согласно которому Ьхд = Ь2, Ъ2д = Ь3, Ь3Я = ЪА,..., Ъп_2 • д = Ьп_х, Ъп_х ■ д = Ьп (см. третью строчку рассуждений); во-вторых, прибавили и вычли отчего значение выражения, разумеется, не изменилось (см. четвертую строчку рассуждений);<br>в-третьих, воспользовались формулой п-го члена геометрической прогрессии:<br>КЯ = (ЪгЯп1)Ч = Ьхд\ Из формулы (1) находим:<br>138<br>4.16.<br>ПРОГРЕССИИ<br>«<7-8 1).<br>3(д- 1) = Ь1(д"-1),<br>5 =<br>_ - 1)<br>9-1<br>Это — формула суммы п членов геометрической прогрессии (для случая, когда д * 1).<br>Пример 8. Дана конечная геометрическая прогрессия «V Ь2, Ъ3,...,Ьп. Известно, что Ьг = 3, д = 2, л = 6. Найти:<br>а) сумму членов прогрессии; б) сумму квадратов ее членов. Р е ш е н и е. а) Имеем<br>= 3(2* - 1) = 3.63 = 189. 6 я - 1 2-1<br>б) Выше (см. с. 132) мы уже отмечали, что если все члены геометрической прогрессии возвести в квадрат, то получится геометрическая прогрессия с первым членом Ь2 и знаменателем д2. Тогда сумма шести членов новой прогрессии будет вычисляться по<br>Ь2((а2)6 -1)<br>формуле 8. = -. Подставив в эту формулу Ъ, = 3, д = 2,<br>0 <7 1<br>получим<br>= 9(212-1) = 3 4()95 = 12 285 в 22 -1 Ответ: а) 189; б) 12 285.<br>Пример 9. Найти 8-й член геометрической прогрессии, у которой Ъх = 3, Ьп = 96, 8п = 189.<br>Решение. Так как Ьп = Ь^"'1, то получаем:<br>96 = Зд"1,<br>_ 32.<br>Далее,<br>8 =<br>д-1 '<br>139<br>4.16. ||<br>ПРОГРЕССИИ<br>Т.е.<br>189 =<br>д-1<br>63(д-1) = д»-1. (2)<br>Выше мы нашли, что д"-1 = 32. Умножив обе части этого равенства на <7, получим д" = 32д. Подставив 32д вместо д" в формулу (2), находим:<br>63(д- 1) = 32д - 1, 31д = 62, д = 2.<br>Зная, что = 3 и д = 2, вычислим Ь8: ЬВ = Ь1-д7, т.е. Ь8 = 3-27 = 384. О т в е т: Ь8 = 384.<br>4. Характеристическое свойство геометрической прогрессии.<br>Пусть дана геометрическая прогрессия Ь2, Ь3, ••■,Ьп, ... . Рассмотрим три ее члена, следующие друг за другом: Ьп1, Ьп, Ьп+1. Известно, что<br>ц л-1<br>ъ Ч = Ъ<br>п* л+1<br>Перемножив эти равенства, получим<br>Ьг =Ь ,6<br>п п-1 Л+1<br>Это значит, что квадрат каждого члена геометрической прогрессии (кроме первого и последнего)равен произведению предшествующего и последующего членов.<br>Верно и обратное: если последовательность (Ьп) такова, что для любого п > 1 выполняется равенство<br>л л-1 л+1'<br>то (Ьп) — геометрическая прогрессия.<br>В самом деле, последнее равенство можно переписать в виде Ь :Ь =Ь .. :Ь .<br>л л-1 л+1 л<br>Это значит, в частности, что Ь2 : = Ь3 : Ь2, Ь3 : Ь2 = Ь4 : Ь3 и т.д. Иными словами, отношение любого члена последовательности к<br>140<br>4.16. ||<br>ПРОГРЕССИИ<br>предшествующему члену всегда одно и то же, а это и означает, что задана геометрическая прогрессия.<br>Фактически мы доказали следующую теорему.<br>Числовая, последовательность является геометрической прогрессией тогда и только тогда, когда квадрат каждого ее члена, кроме первого Теорема (и последнего, в случае конечной последователь-<br>ности ),равен произведению предшествующего и последующего членов (характеристическое свойство геометрической прогрессии ).<br>В предыдущем параграфе мы получили характеристическое свойство арифметической прогрессии: любой ее член равен среднему арифметическому предыдущего и последующего членов. Обратимся теперь к характеристическому свойству геометрической прогрессии и выполним некоторые преобразования равенства<br>Ьг<br>' Ьп-1 Ьп+1-<br>Имеем<br><br>т.е.<br><br>0+1<br>Число л/аЬ называют средним геометрическим чисел а и Ь. Таким образом, последнее равенство означает, что модуль любого члена геометрической прогрессии равен среднему геометрическому предыдущего и последующего членов. В такой формулировке отчетливее обнаруживается аналогия между характеристическими свойствами арифметической и геометрической прогрессий.<br>Пример 10. При каком значении х числа Юх + 7, 4х + 6 и 2х + 3 образуют геометрическую прогрессию?<br>Решение. Согласно характеристическому свойству, заданные выражения должны удовлетворять соотношению<br>(4х + б)2 = (Юзе + 7)(2х + 3). Решая это уравнение, находим:<br>16х2 + 48* + 36 = 20х2 + 44х + 21,<br>141<br>4.16. ||<br>I<br>ПРОГРЕССИИ<br>4хг - - 15 = О, хх = 2,5, х2= 1,5.<br>Подставляя х1 = 2,5 в заданные выражения 10х + 7, 4х + 6, 2х + 3, находим соответственно 32,16, 8. Это — конечная геометрическая прогрессия. Подставляя х2 = -1,5 в заданные выражения 10х + 7, 4х + 6, 2х + 3, находим соответственно -8, 0,0 — это не геометрическая прогрессия.<br>О т в е т: х = 2,5.<br>Завершая разговор о прогрессиях, рассмотрим достаточно сложный пример (из серии так называемых «смешанных задач на прогрессии»).<br>Пример 11. Взяли три числа, которые образуют конечную возрастающую геометрическую прогрессию. Заметили, что если второе число увеличить на 2, а первое и третье числа оставить без изменения, то получится арифметическая прогрессия. Если после этого третье число увеличить на 9, то снова получится геометрическая прогрессия. Какие три числа были взяты сначала?<br>Решение. Первый этап. Составление математической модели.<br>Условия задачи можно кратко записать так:<br>Согласно характеристическому свойству арифметической прогрессии, условие 2) означает, что<br>Согласно характеристическому свойству геометрической прогрессии, условие 3) означает, что<br>1) т4 Ь2, Ь3;<br>2) ^-Ь1,Ь2 + 2, Ь3;<br>3Ь2 + 2,Ь3 + 9.<br>т.е.<br>2(Ь1д + 2) = Ь1 + Ь1д\ 6,(1 + ^-20 = 4.<br>(3)<br>т.е.<br>(Ь2 + 2)2 = Ь1(Ь3 + 9), (Ь1д + 2)2 = Ь1(Ь1д2 + 9),<br>142<br>ПРОГРЕССИИ<br>62д2 + 46,д + 4= б^ + Эб,, 1 6,(9 - 49) = 4. (4)<br>Таким образом, получаем систему двух уравнений ((3) и (4)) с двумя переменными 6, и д:<br>|б,(1 + д2-2д) = 4, |б,(9 - 49) = 4,<br>которая в сочетании с записанным выше условием 1) и представляет собой математическую модель задачи.<br>Второй этап. Работа с составленной моделью. Приравняв левые части обоих уравнений системы, получим: 6,(1 + д2-2д) = 6,(9 -4д), 1 + д2 - 2д = 9 - 4д (мы разделили обе части уравнения на 6,, т.е. на число, отличное от нуля). Далее имеем<br>д2 + 2д-8 = 0, д, = 2, д2 = -4.<br>Подставив значение д = 2 во второе уравнение системы, получим 6, = 4. Зная 6, и д, нетрудно записать три числа, образующие геометрическую прогрессию: 4,8,16.<br>Подставив значение д = -4 во второе уравнение системы, полу-<br>4<br>чим = 25 • Зная 6, и д, нетрудно записать три числа, образующие<br>4 16 64 геометрическую прогрессию: т^ . _25 ' 25 '<br>Третий этап. Ответ на вопрос задачи.<br>Из двух найденных геометрических прогрессий только первая является возрастающей, как того требует условие задачи. О т в е т: 4, 8, 16.
| + | [[Image:Al91733.jpg]]<br>[[Image:al91734.jpg]]<br>Так как 512 = 2<sup>9</sup>, то получаем п - 1 = 9, п = 10. |
| | + | |
| | + | в) Имеем |
| | + | |
| | + | [[Image:al91735.jpg]]<br>г) Имеем |
| | + | |
| | + | [[Image:al91736.jpg]]<br>'''Пример 7.''' Разность между седьмым и пятым членами геометрической прогрессии равна 48, сумма пятого и шестого членов прогрессии также равна 48. Найти двенадцатый член этой прогрессии.<br>'''Решение. Первый этап.''' Составление математической модели.<br>Условия задачи можно кратко записать так:<br>[[Image:al91737.jpg]]<br>Воспользовавшись формулой п-го члена геометрической прогрессии, получим:[[Image:al91738.jpg]]<br>Тогда второе условие задачи (Ь<sub>7</sub> - Ь<sub>5</sub> = 48) можно записать в виде |
| | + | |
| | + | [[Image:al91739.jpg]]<br>Третье условие задачи (Ь<sub>5</sub> + Ь<sub>6</sub> = 48) можно записать в виде |
| | + | |
| | + | [[Image:al91740.jpg]]<br>В итоге получаем систему двух уравнений с двумя переменными Ь<sub>1</sub> и q: |
| | + | |
| | + | [[Image:al91741.jpg]]<br>которая в сочетании с записанным выше условием 1) и представляет собой математическую модель задачи.<br>'''Второй этап.''' Работа с составленной моделью. Приравняв левые части обоих уравнений системы, получим: |
| | + | |
| | + | [[Image:al91742.jpg]]<br>(мы разделили обе части уравнения на выражение Ъ<sub>1</sub>q<sup>4</sup>, отличное от нуля).<br>Из уравнения q<sub>2</sub> - q - 2 = 0 находим q<sub>1</sub> = 2, q<sup>2</sup> = -1. Подставив значение q = 2 во второе уравнение системы, получим [[Image:al91743.jpg]]<br>Подставив значение q = -1 во второе уравнение системы, получим Ь<sub>1</sub> • 1 • 0 = 48; это уравнение не имеет решений.<br>Итак, b<sub>1</sub>=1, q = 2 — эта пара является решением составленной системы уравнений.<br>Теперь мы можем записать геометрическую прогрессию, о которой идет речь в задаче: 1, 2, 4, 8, 16, 32, ... .<br>'''Третий этап.''' Ответ на вопрос задачи. Требуется вычислить b<sub>12</sub>. Имеем |
| | + | |
| | + | [[Image:al91744.jpg]]<br>О т в е т: b<sub>12</sub> = 2048.<br>137<br>4.16. ||<br>ПРОГРЕССИИ<br>3. Формула суммы членов конечной геометрической прогрессии.<br>Пусть дана конечная геометрическая прогрессия<br>Н ь1,ь2,ь3,...,ъп_2,ъп_1,ьп.<br>Обозначим через 5 сумму ее членов, т.е.<br>8п = Ь1 + Ь2 + Ъ3 +<br>+ ь. + ьп. + ь<br>П-2 Л-1 Л<br>Выведем формулу для отыскания этой суммы.<br>Начнем с самого простого случая, когда д = 1. Тогда геометрическая прогрессия Ьх, Ь2, Ь3,..., Ъп состоит из п чисел, равных Ъх, т.е. прогрессия имеет вид Ъх, Ъх, Ъх, ..., Ьх. Сумма этих чисел равна пЪх.<br>Пусть теперь д Ф 1. Для отыскания <§п применим искусственный прием: выполним некоторые преобразования выражения 8д. Имеем:<br>5 д = (Ьх + Ь2 + Ь3 + ... + Ъп 2 + Ь^ + Ьп)д = = Ьхц + Ь2д + &3д + ... + Ьп2д + Ъп_хд + Ь„д = = + + Ь. + ... + & , + Ь + Ьа =<br>2 3 4 п-1 п л*<br>4 1 2 3 п-2 п-1 п' п1 1<br>= 5 + &д-& =5 +(Ь -д^-д-Ь =5 +Ь,дп-Ь,.<br>п 1 п у 1 ^ ' * 1 п 1<br>Итак, мы доказали, что<br>5 д = 8 + 6,д" - Ь,.<br>п* п I* 1<br>(1)<br>Выполняя преобразования, мы, во-первых, пользовались определением геометрической прогрессии, согласно которому Ьхд = Ь2, Ъ2д = Ь3, Ь3Я = ЪА,..., Ъп_2 • д = Ьп_х, Ъп_х ■ д = Ьп (см. третью строчку рассуждений); во-вторых, прибавили и вычли отчего значение выражения, разумеется, не изменилось (см. четвертую строчку рассуждений);<br>в-третьих, воспользовались формулой п-го члена геометрической прогрессии:<br>КЯ = (ЪгЯп1)Ч = Ьхд\ Из формулы (1) находим:<br>138<br>4.16.<br>ПРОГРЕССИИ<br>«<7-8 1).<br>3(д- 1) = Ь1(д"-1),<br>5 =<br>_ - 1)<br>9-1<br>Это — формула суммы п членов геометрической прогрессии (для случая, когда д * 1).<br>Пример 8. Дана конечная геометрическая прогрессия «V Ь2, Ъ3,...,Ьп. Известно, что Ьг = 3, д = 2, л = 6. Найти:<br>а) сумму членов прогрессии; б) сумму квадратов ее членов. Р е ш е н и е. а) Имеем<br>= 3(2* - 1) = 3.63 = 189. 6 я - 1 2-1<br>б) Выше (см. с. 132) мы уже отмечали, что если все члены геометрической прогрессии возвести в квадрат, то получится геометрическая прогрессия с первым членом Ь2 и знаменателем д2. Тогда сумма шести членов новой прогрессии будет вычисляться по<br>Ь2((а2)6 -1)<br>формуле 8. = -. Подставив в эту формулу Ъ, = 3, д = 2,<br>0 <7 1<br>получим<br>= 9(212-1) = 3 4()95 = 12 285 в 22 -1 Ответ: а) 189; б) 12 285.<br>Пример 9. Найти 8-й член геометрической прогрессии, у которой Ъх = 3, Ьп = 96, 8п = 189.<br>Решение. Так как Ьп = Ь^"'1, то получаем:<br>96 = Зд"1,<br>_ 32.<br>Далее,<br>8 =<br>д-1 '<br>139<br>4.16. ||<br>ПРОГРЕССИИ<br>Т.е.<br>189 =<br>д-1<br>63(д-1) = д»-1. (2)<br>Выше мы нашли, что д"-1 = 32. Умножив обе части этого равенства на <7, получим д" = 32д. Подставив 32д вместо д" в формулу (2), находим:<br>63(д- 1) = 32д - 1, 31д = 62, д = 2.<br>Зная, что = 3 и д = 2, вычислим Ь8: ЬВ = Ь1-д7, т.е. Ь8 = 3-27 = 384. О т в е т: Ь8 = 384.<br>4. Характеристическое свойство геометрической прогрессии.<br>Пусть дана геометрическая прогрессия Ь2, Ь3, ••■,Ьп, ... . Рассмотрим три ее члена, следующие друг за другом: Ьп1, Ьп, Ьп+1. Известно, что<br>ц л-1<br>ъ Ч = Ъ<br>п* л+1<br>Перемножив эти равенства, получим<br>Ьг =Ь ,6<br>п п-1 Л+1<br>Это значит, что квадрат каждого члена геометрической прогрессии (кроме первого и последнего)равен произведению предшествующего и последующего членов.<br>Верно и обратное: если последовательность (Ьп) такова, что для любого п > 1 выполняется равенство<br>л л-1 л+1'<br>то (Ьп) — геометрическая прогрессия.<br>В самом деле, последнее равенство можно переписать в виде Ь :Ь =Ь .. :Ь .<br>л л-1 л+1 л<br>Это значит, в частности, что Ь2 : = Ь3 : Ь2, Ь3 : Ь2 = Ь4 : Ь3 и т.д. Иными словами, отношение любого члена последовательности к<br>140<br>4.16. ||<br>ПРОГРЕССИИ<br>предшествующему члену всегда одно и то же, а это и означает, что задана геометрическая прогрессия.<br>Фактически мы доказали следующую теорему.<br>Числовая, последовательность является геометрической прогрессией тогда и только тогда, когда квадрат каждого ее члена, кроме первого Теорема (и последнего, в случае конечной последователь-<br>ности ),равен произведению предшествующего и последующего членов (характеристическое свойство геометрической прогрессии ).<br>В предыдущем параграфе мы получили характеристическое свойство арифметической прогрессии: любой ее член равен среднему арифметическому предыдущего и последующего членов. Обратимся теперь к характеристическому свойству геометрической прогрессии и выполним некоторые преобразования равенства<br>Ьг<br>' Ьп-1 Ьп+1-<br>Имеем<br><br>т.е.<br><br>0+1<br>Число л/аЬ называют средним геометрическим чисел а и Ь. Таким образом, последнее равенство означает, что модуль любого члена геометрической прогрессии равен среднему геометрическому предыдущего и последующего членов. В такой формулировке отчетливее обнаруживается аналогия между характеристическими свойствами арифметической и геометрической прогрессий.<br>Пример 10. При каком значении х числа Юх + 7, 4х + 6 и 2х + 3 образуют геометрическую прогрессию?<br>Решение. Согласно характеристическому свойству, заданные выражения должны удовлетворять соотношению<br>(4х + б)2 = (Юзе + 7)(2х + 3). Решая это уравнение, находим:<br>16х2 + 48* + 36 = 20х2 + 44х + 21,<br>141<br>4.16. ||<br>I<br>ПРОГРЕССИИ<br>4хг - - 15 = О, хх = 2,5, х2= 1,5.<br>Подставляя х1 = 2,5 в заданные выражения 10х + 7, 4х + 6, 2х + 3, находим соответственно 32,16, 8. Это — конечная геометрическая прогрессия. Подставляя х2 = -1,5 в заданные выражения 10х + 7, 4х + 6, 2х + 3, находим соответственно -8, 0,0 — это не геометрическая прогрессия.<br>О т в е т: х = 2,5.<br>Завершая разговор о прогрессиях, рассмотрим достаточно сложный пример (из серии так называемых «смешанных задач на прогрессии»).<br>Пример 11. Взяли три числа, которые образуют конечную возрастающую геометрическую прогрессию. Заметили, что если второе число увеличить на 2, а первое и третье числа оставить без изменения, то получится арифметическая прогрессия. Если после этого третье число увеличить на 9, то снова получится геометрическая прогрессия. Какие три числа были взяты сначала?<br>Решение. Первый этап. Составление математической модели.<br>Условия задачи можно кратко записать так:<br>Согласно характеристическому свойству арифметической прогрессии, условие 2) означает, что<br>Согласно характеристическому свойству геометрической прогрессии, условие 3) означает, что<br>1) т4 Ь2, Ь3;<br>2) ^-Ь1,Ь2 + 2, Ь3;<br>3Ь2 + 2,Ь3 + 9.<br>т.е.<br>2(Ь1д + 2) = Ь1 + Ь1д\ 6,(1 + ^-20 = 4.<br>(3)<br>т.е.<br>(Ь2 + 2)2 = Ь1(Ь3 + 9), (Ь1д + 2)2 = Ь1(Ь1д2 + 9),<br>142<br>ПРОГРЕССИИ<br>62д2 + 46,д + 4= б^ + Эб,, 1 6,(9 - 49) = 4. (4)<br>Таким образом, получаем систему двух уравнений ((3) и (4)) с двумя переменными 6, и д:<br>|б,(1 + д2-2д) = 4, |б,(9 - 49) = 4,<br>которая в сочетании с записанным выше условием 1) и представляет собой математическую модель задачи.<br>Второй этап. Работа с составленной моделью. Приравняв левые части обоих уравнений системы, получим: 6,(1 + д2-2д) = 6,(9 -4д), 1 + д2 - 2д = 9 - 4д (мы разделили обе части уравнения на 6,, т.е. на число, отличное от нуля). Далее имеем<br>д2 + 2д-8 = 0, д, = 2, д2 = -4.<br>Подставив значение д = 2 во второе уравнение системы, получим 6, = 4. Зная 6, и д, нетрудно записать три числа, образующие геометрическую прогрессию: 4,8,16.<br>Подставив значение д = -4 во второе уравнение системы, полу-<br>4<br>чим = 25 • Зная 6, и д, нетрудно записать три числа, образующие<br>4 16 64 геометрическую прогрессию: т^ . _25 ' 25 '<br>Третий этап. Ответ на вопрос задачи.<br>Из двух найденных геометрических прогрессий только первая является возрастающей, как того требует условие задачи. О т в е т: 4, 8, 16. |
| | | | |
| | А.Г. Мордкович Алгебра 9 класс | | А.Г. Мордкович Алгебра 9 класс |
Версия 12:38, 1 июля 2010
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Геометрическая прогрессия
ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
Для удобства читателя этот параграф строится точно по тому же плану, которого мы придерживались в предыдущем параграфе.
1. Основные понятия.
Определение. Числовую последовательность, все члены которой отличны от 0 и каждый член которой, начиная со второго, получается из предыдущего члена умножением его на одно и то же число называют геометрической прогрессией. При этом число 5 называют знаменателем геометрической прогрессии.
Таким образом, геометрическая прогрессия — это числовая последовательность (bn), заданная рекуррентно соотношениями
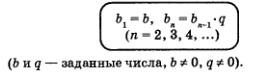
Можно ли, глядя на числовую последовательность, определить, является ли она геометрической прогрессией? Можно. Если вы убедились в том, что
отношение любого члена последовательности к предыдущему члену постоянно 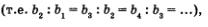 то перед вами— геометрическая прогрессия. то перед вами— геометрическая прогрессия.
Пример 1. 1, 3, 9, 27, 81,... .
Это геометрическая прогрессия, у которой Ь1 = 1, q = 3.
Пример 2. 
Это геометрическая прогрессия, у которой 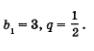
Пример 3. 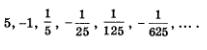
Это геометрическая прогрессия, у которой 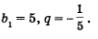
Пример 4. 8, 8, 8, 8, 8, 8,....
Это геометрическая прогрессия, у которой b1 — 8, q = 1.
Заметим, что эта последовательность является и арифметической прогрессией (см. пример 3 из § 15).
Пример 5. 2,-2,2,-2,2,-2.....
Это геометрическая прогрессия, у которой b1 = 2, q = -1.
Очевидно, что геометрическая прогрессия является возрастающей последовательностью, если b1 > 0, q > 1 (см. пример 1), и убывающей, если b1> 0, 0 < q < 1 (см. пример 2).
Для обозначения того, что последовательность (bn) является геометрической прогрессией, иногда бывает удобна следующая запись:
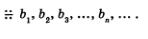
Значок 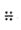 заменяет словосочетание «геометрическая прогрессия». заменяет словосочетание «геометрическая прогрессия».
Отметим одно любопытное и в то же время достаточно очевидное свойство геометрической прогрессии:
Если последовательность 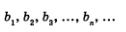 является геометрической прогрессией, то и последовательность квадратов, т.е. является геометрической прогрессией, то и последовательность квадратов, т.е. 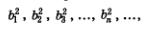 является геометрической прогрессией. является геометрической прогрессией.
У второй геометрической прогрессии первый член равен 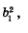 а знаменатель равен q2. а знаменатель равен q2.
Если в геометрической прогрессии отбросить все члены, следующие за bn, то получится конечная геометрическая прогрессия 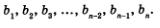
В дальнейших пунктах этого параграфа мы рассмотрим наиболее важные свойства геометрической прогрессии.
2. Формула п-го члена геометрической прогрессии.
Рассмотрим геометрическую прогрессию 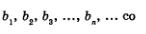 со знаменателем q. Имеем: со знаменателем q. Имеем:
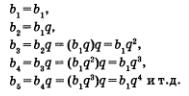
Нетрудно догадаться, что для любого номера п справедливо равенство

Это — формула п-го члена геометрической прогрессии.
Замечание. Если вы прочли важное замечание из предыдущего параграфа и поняли его, то попробуйте доказать формулу (1) методом математической индукции подобно тому, как зто было сделано для формулы п-го члена арифметической прогрессии.
Перепишем формулу п-го члена геометрической прогрессии
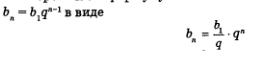
и введем обозначения: 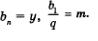 Получим у = mq2, или, подробнее, Получим у = mq2, или, подробнее, 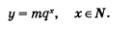
Аргумент х содержится в показателе степени, поэтому такую функцию называют показательной функцией. Значит, геометрическую прогрессию можно рассматривать как показательную функцию, заданную на множестве N натуральных чисел. На рис. 96а изображен график функции 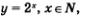 рис. 966 — график функции рис. 966 — график функции 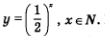 В обоих случаях имеем изолированные точки В обоих случаях имеем изолированные точки
(с абсциссами х= 1, х = 2, х = 3 и т.д.), лежащие на некоторой кривой (на обоих рисунках представлена одна и та же кривая, только по-разному расположенная и изображенная в разных масштабах). Эту кривую называют экспонентой. Подробнее о показательной функции и ее графике речь пойдет в курсе алгебры 11-го класса.
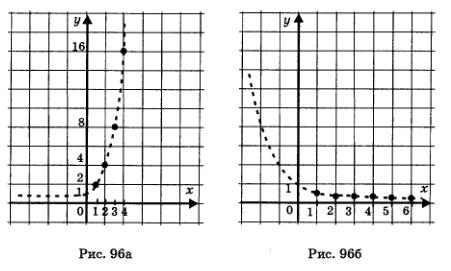
Вернемся к примерам 1—5 из предыдущего пункта.
1) 1, 3, 9, 27, 81,... . Это геометрическая прогрессия, у которой Ь1 = 1, q = 3. Составим формулу п-го члена 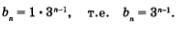
2) 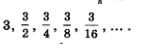 Это геометрическая прогрессия, у которой Это геометрическая прогрессия, у которой 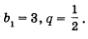 Составим формулу п-го члена Составим формулу п-го члена
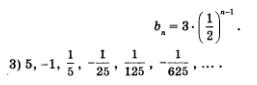
Это геометрическая прогрессия, у которой 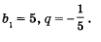 Составим формулу п-го члена Составим формулу п-го члена 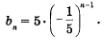
4) 8, 8, 8, ..., 8, ... . Это геометрическая прогрессия, у которой Ь1 = 8, q = 1. Составим формулу п-го члена 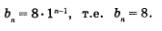
5) 2, -2, 2, -2, 2, -2,.... Это геометрическая прогрессия, у которой Ъ1 = 2, q = —1. Составим формулу п-го члена 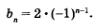
Пример 6. Дана геометрическая прогрессия
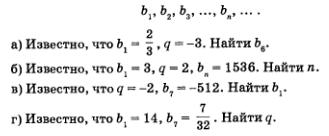
Р е ш е н и е. Во всех случаях в основе решения лежит формула п-го члена геометрической прогрессии
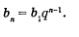
а) Положив в формуле п-го члена геометрической прогрессии п = 6, получим
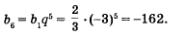
б) Имеем
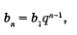

Так как 512 = 29, то получаем п - 1 = 9, п = 10.
в) Имеем
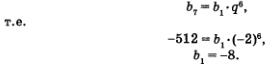
г) Имеем
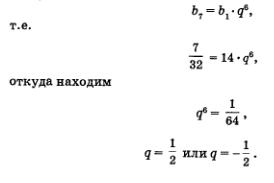
Пример 7. Разность между седьмым и пятым членами геометрической прогрессии равна 48, сумма пятого и шестого членов прогрессии также равна 48. Найти двенадцатый член этой прогрессии.
Решение. Первый этап. Составление математической модели.
Условия задачи можно кратко записать так:
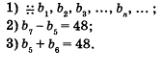
Воспользовавшись формулой п-го члена геометрической прогрессии, получим: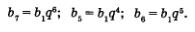
Тогда второе условие задачи (Ь7 - Ь5 = 48) можно записать в виде
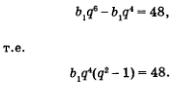
Третье условие задачи (Ь5 + Ь6 = 48) можно записать в виде
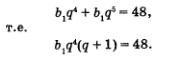
В итоге получаем систему двух уравнений с двумя переменными Ь1 и q:
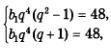
которая в сочетании с записанным выше условием 1) и представляет собой математическую модель задачи.
Второй этап. Работа с составленной моделью. Приравняв левые части обоих уравнений системы, получим:
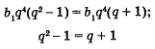
(мы разделили обе части уравнения на выражение Ъ1q4, отличное от нуля).
Из уравнения q2 - q - 2 = 0 находим q1 = 2, q2 = -1. Подставив значение q = 2 во второе уравнение системы, получим 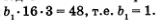
Подставив значение q = -1 во второе уравнение системы, получим Ь1 • 1 • 0 = 48; это уравнение не имеет решений.
Итак, b1=1, q = 2 — эта пара является решением составленной системы уравнений.
Теперь мы можем записать геометрическую прогрессию, о которой идет речь в задаче: 1, 2, 4, 8, 16, 32, ... .
Третий этап. Ответ на вопрос задачи. Требуется вычислить b12. Имеем
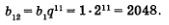
О т в е т: b12 = 2048.
137
4.16. ||
ПРОГРЕССИИ
3. Формула суммы членов конечной геометрической прогрессии.
Пусть дана конечная геометрическая прогрессия
Н ь1,ь2,ь3,...,ъп_2,ъп_1,ьп.
Обозначим через 5 сумму ее членов, т.е.
8п = Ь1 + Ь2 + Ъ3 +
+ ь. + ьп. + ь
П-2 Л-1 Л
Выведем формулу для отыскания этой суммы.
Начнем с самого простого случая, когда д = 1. Тогда геометрическая прогрессия Ьх, Ь2, Ь3,..., Ъп состоит из п чисел, равных Ъх, т.е. прогрессия имеет вид Ъх, Ъх, Ъх, ..., Ьх. Сумма этих чисел равна пЪх.
Пусть теперь д Ф 1. Для отыскания <§п применим искусственный прием: выполним некоторые преобразования выражения 8д. Имеем:
5 д = (Ьх + Ь2 + Ь3 + ... + Ъп 2 + Ь^ + Ьп)д = = Ьхц + Ь2д + &3д + ... + Ьп2д + Ъп_хд + Ь„д = = + + Ь. + ... + & , + Ь + Ьа =
2 3 4 п-1 п л*
4 1 2 3 п-2 п-1 п' п1 1
= 5 + &д-& =5 +(Ь -д^-д-Ь =5 +Ь,дп-Ь,.
п 1 п у 1 ^ ' * 1 п 1
Итак, мы доказали, что
5 д = 8 + 6,д" - Ь,.
п* п I* 1
(1)
Выполняя преобразования, мы, во-первых, пользовались определением геометрической прогрессии, согласно которому Ьхд = Ь2, Ъ2д = Ь3, Ь3Я = ЪА,..., Ъп_2 • д = Ьп_х, Ъп_х ■ д = Ьп (см. третью строчку рассуждений); во-вторых, прибавили и вычли отчего значение выражения, разумеется, не изменилось (см. четвертую строчку рассуждений);
в-третьих, воспользовались формулой п-го члена геометрической прогрессии:
КЯ = (ЪгЯп1)Ч = Ьхд\ Из формулы (1) находим:
138
4.16.
ПРОГРЕССИИ
«<7-8 1).
3(д- 1) = Ь1(д"-1),
5 =
_ - 1)
9-1
Это — формула суммы п членов геометрической прогрессии (для случая, когда д * 1).
Пример 8. Дана конечная геометрическая прогрессия «V Ь2, Ъ3,...,Ьп. Известно, что Ьг = 3, д = 2, л = 6. Найти:
а) сумму членов прогрессии; б) сумму квадратов ее членов. Р е ш е н и е. а) Имеем
= 3(2* - 1) = 3.63 = 189. 6 я - 1 2-1
б) Выше (см. с. 132) мы уже отмечали, что если все члены геометрической прогрессии возвести в квадрат, то получится геометрическая прогрессия с первым членом Ь2 и знаменателем д2. Тогда сумма шести членов новой прогрессии будет вычисляться по
Ь2((а2)6 -1)
формуле 8. = -. Подставив в эту формулу Ъ, = 3, д = 2,
0 <7 1
получим
= 9(212-1) = 3 4()95 = 12 285 в 22 -1 Ответ: а) 189; б) 12 285.
Пример 9. Найти 8-й член геометрической прогрессии, у которой Ъх = 3, Ьп = 96, 8п = 189.
Решение. Так как Ьп = Ь^"'1, то получаем:
96 = Зд"1,
_ 32.
Далее,
8 =
д-1 '
139
4.16. ||
ПРОГРЕССИИ
Т.е.
189 =
д-1
63(д-1) = д»-1. (2)
Выше мы нашли, что д"-1 = 32. Умножив обе части этого равенства на <7, получим д" = 32д. Подставив 32д вместо д" в формулу (2), находим:
63(д- 1) = 32д - 1, 31д = 62, д = 2.
Зная, что = 3 и д = 2, вычислим Ь8: ЬВ = Ь1-д7, т.е. Ь8 = 3-27 = 384. О т в е т: Ь8 = 384.
4. Характеристическое свойство геометрической прогрессии.
Пусть дана геометрическая прогрессия Ь2, Ь3, ••■,Ьп, ... . Рассмотрим три ее члена, следующие друг за другом: Ьп1, Ьп, Ьп+1. Известно, что
ц л-1
ъ Ч = Ъ
п* л+1
Перемножив эти равенства, получим
Ьг =Ь ,6
п п-1 Л+1
Это значит, что квадрат каждого члена геометрической прогрессии (кроме первого и последнего)равен произведению предшествующего и последующего членов.
Верно и обратное: если последовательность (Ьп) такова, что для любого п > 1 выполняется равенство
л л-1 л+1'
то (Ьп) — геометрическая прогрессия.
В самом деле, последнее равенство можно переписать в виде Ь :Ь =Ь .. :Ь .
л л-1 л+1 л
Это значит, в частности, что Ь2 : = Ь3 : Ь2, Ь3 : Ь2 = Ь4 : Ь3 и т.д. Иными словами, отношение любого члена последовательности к
140
4.16. ||
ПРОГРЕССИИ
предшествующему члену всегда одно и то же, а это и означает, что задана геометрическая прогрессия.
Фактически мы доказали следующую теорему.
Числовая, последовательность является геометрической прогрессией тогда и только тогда, когда квадрат каждого ее члена, кроме первого Теорема (и последнего, в случае конечной последователь-
ности ),равен произведению предшествующего и последующего членов (характеристическое свойство геометрической прогрессии ).
В предыдущем параграфе мы получили характеристическое свойство арифметической прогрессии: любой ее член равен среднему арифметическому предыдущего и последующего членов. Обратимся теперь к характеристическому свойству геометрической прогрессии и выполним некоторые преобразования равенства
Ьг
' Ьп-1 Ьп+1-
Имеем
т.е.
0+1
Число л/аЬ называют средним геометрическим чисел а и Ь. Таким образом, последнее равенство означает, что модуль любого члена геометрической прогрессии равен среднему геометрическому предыдущего и последующего членов. В такой формулировке отчетливее обнаруживается аналогия между характеристическими свойствами арифметической и геометрической прогрессий.
Пример 10. При каком значении х числа Юх + 7, 4х + 6 и 2х + 3 образуют геометрическую прогрессию?
Решение. Согласно характеристическому свойству, заданные выражения должны удовлетворять соотношению
(4х + б)2 = (Юзе + 7)(2х + 3). Решая это уравнение, находим:
16х2 + 48* + 36 = 20х2 + 44х + 21,
141
4.16. ||
I
ПРОГРЕССИИ
4хг - - 15 = О, хх = 2,5, х2= 1,5.
Подставляя х1 = 2,5 в заданные выражения 10х + 7, 4х + 6, 2х + 3, находим соответственно 32,16, 8. Это — конечная геометрическая прогрессия. Подставляя х2 = -1,5 в заданные выражения 10х + 7, 4х + 6, 2х + 3, находим соответственно -8, 0,0 — это не геометрическая прогрессия.
О т в е т: х = 2,5.
Завершая разговор о прогрессиях, рассмотрим достаточно сложный пример (из серии так называемых «смешанных задач на прогрессии»).
Пример 11. Взяли три числа, которые образуют конечную возрастающую геометрическую прогрессию. Заметили, что если второе число увеличить на 2, а первое и третье числа оставить без изменения, то получится арифметическая прогрессия. Если после этого третье число увеличить на 9, то снова получится геометрическая прогрессия. Какие три числа были взяты сначала?
Решение. Первый этап. Составление математической модели.
Условия задачи можно кратко записать так:
Согласно характеристическому свойству арифметической прогрессии, условие 2) означает, что
Согласно характеристическому свойству геометрической прогрессии, условие 3) означает, что
1) т4 Ь2, Ь3;
2) ^-Ь1,Ь2 + 2, Ь3;
3Ь2 + 2,Ь3 + 9.
т.е.
2(Ь1д + 2) = Ь1 + Ь1д\ 6,(1 + ^-20 = 4.
(3)
т.е.
(Ь2 + 2)2 = Ь1(Ь3 + 9), (Ь1д + 2)2 = Ь1(Ь1д2 + 9),
142
ПРОГРЕССИИ
62д2 + 46,д + 4= б^ + Эб,, 1 6,(9 - 49) = 4. (4)
Таким образом, получаем систему двух уравнений ((3) и (4)) с двумя переменными 6, и д:
|б,(1 + д2-2д) = 4, |б,(9 - 49) = 4,
которая в сочетании с записанным выше условием 1) и представляет собой математическую модель задачи.
Второй этап. Работа с составленной моделью. Приравняв левые части обоих уравнений системы, получим: 6,(1 + д2-2д) = 6,(9 -4д), 1 + д2 - 2д = 9 - 4д (мы разделили обе части уравнения на 6,, т.е. на число, отличное от нуля). Далее имеем
д2 + 2д-8 = 0, д, = 2, д2 = -4.
Подставив значение д = 2 во второе уравнение системы, получим 6, = 4. Зная 6, и д, нетрудно записать три числа, образующие геометрическую прогрессию: 4,8,16.
Подставив значение д = -4 во второе уравнение системы, полу-
4
чим = 25 • Зная 6, и д, нетрудно записать три числа, образующие
4 16 64 геометрическую прогрессию: т^ . _25 ' 25 '
Третий этап. Ответ на вопрос задачи.
Из двух найденных геометрических прогрессий только первая является возрастающей, как того требует условие задачи. О т в е т: 4, 8, 16.
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|