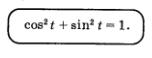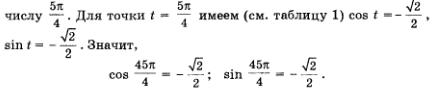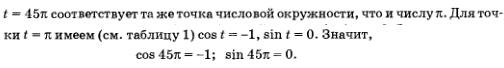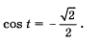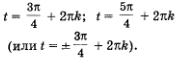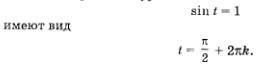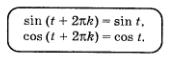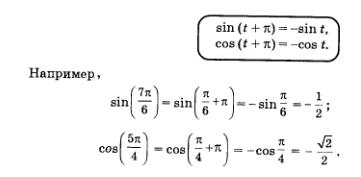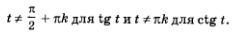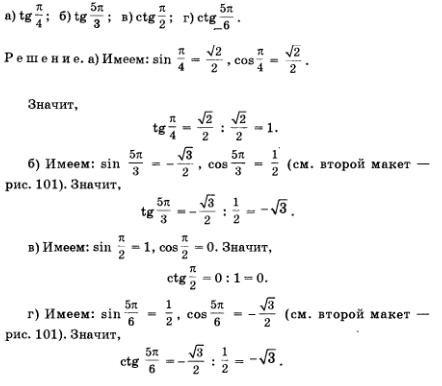|
|
|
| Строка 1: |
Строка 1: |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Синус и косинус. Тангенс и котангенс<metakeywords>Синус и косинус. Тангенс и котангенс</metakeywords>''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика: Синус и косинус. Тангенс и котангенс<metakeywords>Синус, косинус, Тангенс, котангенс, числовой окружности, координаты, синуса, уравнение, точки, косинусе, окружности, модулю, тангенса</metakeywords>''' |
| | | | |
| - | <br> | + | <br> '''Синус и косинус. Тангенс и котангенс.'''<br> |
| | | | |
| - | СИНУС И КОСИНУС. ТАНГЕНС И КОТАНГЕНС.<br>'''1.''' Синус и косинус.<br>Определение. Если точка М числовой окружности соответствует числу t, то абсциссу точки М называют косинусом числа t и обозначают соз t, а ординату точки М называют синусом числа t и обозначают зт t.<br>Итак (см.рис. 109),
| + | '''<br>1. Синус и косинус.'''<br> |
| | | | |
| - | [[Image:Alg31.jpg]]<br>Вооружившись определением, вернемся к предыдущему параграфу и как бы заново перечитаем его.<br>Мы отметили в § 18, что каждая точка числовой окружности имеет в системе хОу свои координаты, причем: | + | '''Определение'''. Если точка М [[2. Числовая окружность|числовой окружности]] соответствует числу t, то абсциссу точки М называют косинусом числа t и обозначают соs t, а ординату точки М называют синусом числа t и обозначают sin t.<br> |
| | | | |
| - | у точек первой четверти х > 0, у > 0;<br>у точек второй четверти х < 0, у > 0;<br>у точек третьей четверти х < 0, у < 0;<br>у точек четвертой четверти х > 0, у < 0 (рис. 104).<br>Это позволяет нам составить соответствующую таблицу знаков синуса и косинуса по четвертям числовой окружности:
| + | Итак (см.рис. 109),<br> |
| | | | |
| - | [[Image:Alg32.jpg]]<br>Мы отметили в § 18, что уравнение числовой окружности имеет вид х<sup>2</sup> + у<sup>2</sup> = 1.<br>Тем самым фактически получено важное равенство, связывающее ат t и соз t:<br>[[Image:Alg33.jpg]]<br>В § 18 было отмечено, как важно научиться отыскивать координаты точек числовой окружности, прежде всего тех, что представлены на первом и втором макетах (рис. 100 и 101). Теперь эта мысль стала, думается, предельно ясной: опираясь на таблицы 1 и 2 из § 18, мы без труда составим соответствующие таблицы для вычисления значений соа t и ат t. | + | [[Image:Alg31.jpg|240px|Синус и косинус]]<br> |
| | | | |
| - | [[Image:Alg34.jpg]]<br>'''Пример 1.''' Вычислить соs t и sin t, если:
| + | <br>Вооружившись определением, вернемся к предыдущему параграфу и как бы заново перечитаем его.<br> |
| | | | |
| - | [[Image:Alg35.jpg]]<br>'''Решение:''' '''а)''' В примере 1а из § 18 мы установили, что числу [[Image:Alg36.jpg]] соответствует та же точка числовой окружности, что и
| + | Мы отметили в § 18, что каждая точка числовой окружности имеет в системе хОу свои [[Шкалы и координаты|координаты]], причем: |
| | | | |
| - | [[Image:Alg37.jpg]]<br>'''б) ''' В примере 16 из § 18 мы установили, что числу
| + | у точек первой четверти х > 0, у > 0;<br>у точек второй четверти х < 0, у > 0;<br>у точек третьей четверти х < 0, у < 0;<br>у точек четвертой четверти х > 0, у < 0 (рис. 104).<br> |
| | | | |
| - | [[Image:Alg38.jpg]] <br>'''Пример 2.''' Решить уравнение [[Image:Alg39.jpg]]<br> | + | Это позволяет нам составить соответствующую таблицу знаков [[4. Синус и косинус|синуса]] и косинуса по четвертям числовой окружности: |
| | | | |
| - | '''Решение.''' Учтем, что sin t — ордината точки М{<sub>1</sub>) числовой окружности. Значит, нам нужно найти на числовой окружности 1<br>точки с ординатой - и записать, каким числам I они соответствуют. Но эта задача уже решена выше — см. пример 2 из § 18:
| + | [[Image:Alg32.jpg|240px|Таблица]]<br> |
| | | | |
| - | [[Image:Alg310.jpg]]<br>'''Пример 3.''' Решить уравнение [[Image:Alg311.jpg]]<br>'''Решение.''' Учтем, что sin t — ордината точки М{<sub>1</sub>) числовой окружности. Значит, нам нужно найти на числовой окружности 1<br> точки с ординатой - и записать, каким числам I они соответствуют. Но эта задача уже решена выше — см. пример 3 из § 18:
| + | Мы отметили в § 18, что уравнение числовой окружности имеет вид х<sup>2</sup> + у<sup>2</sup> = 1.<br> |
| | | | |
| - | [[Image:Alg312.jpg]]<br>'''Пример 4.''' Решить уравнение: | + | Тем самым фактически получено важное равенство, связывающее sin t и соs t:<br>[[Image:Alg33.jpg|180px|Формула]]<br>В § 18 было отмечено, как важно научиться отыскивать координаты точек числовой окружности, прежде всего тех, что представлены на первом и втором макетах (рис. 100 и 101). Теперь эта мысль стала, думается, предельно ясной: опираясь на таблицы 1 и 2 из § 18, мы без труда составим соответствующие таблицы для вычисления значений соs t и sin t. |
| | | | |
| - | [[Image:Alg313.jpg]]<br>'''Р е ш е н и е. а) '''Нам нужно найти на числовой окружности точки с ординатой 0 и записать, каким числам I они соответствуют. Ординату 0 имеют точки А и С (рис. 109), они соответствуют числам 0 (точкаА), п (точка С), 2п (точка А), Зп (точка С), -п (точка С), -2л (точка А) и т.д. Короче это можно записать так: точки А и С соответствуют числам вида пк. | + | [[Image:Alg34.jpg|480px|Таблицы]]<br>'''Пример 1.''' <br> |
| | | | |
| - | [[Image:Alg314.jpg]]<br>
| + | Вычислить соs t и sin t, если: |
| | | | |
| - | '''б) ''' Ординату 1 имеет точка В числовой окружности (рис. 109). <br> Значит, решения уравнения
| + | [[Image:Alg35.jpg|320px|Пример]]<br> |
| | | | |
| - | [[Image:Alg315.jpg]]<br>'''Замечание.''' Напомним еще раз о нашей договоренности: параметр к (или п) принимает любые целочисленные значения (к е 2 ), мы это постоянно подразумеваем, но, краткости ради, не записываем.<br>Завершая разговор о синусе и косинусе, остановимся на их свойствах.<br>'''Свойство 1.''' Для любого значения I справедливы равенства:
| + | <br>'''Решение:'''<br> |
| | | | |
| - | [[Image:Alg316.jpg]]<br>Доказательство. Если числу t соответствует точка М числовой окружности, то числу -1 соответствует точка Р, симметричная точке М относительно горизонтального диаметра окружности (рис. 110), т.е. симметричная точке М относительно оси абсцисс. У таких точек одна и та же абсцисса, а это значит, что сое (-t) = = соs t. У таких точек равные по модулю, но противоположные по знаку ординаты; это значит, что sin (-t) = cos t.<br>'''Свойство 2.''' Для любого значения 1: справедливы равенства | + | а) В примере 1а из § 18 мы установили, что числу [[Image:Alg36.jpg|Решение]] соответствует та же точка числовой окружности, что и |
| | | | |
| - | [[Image:Alg317.jpg]]<br>Это очевидно, поскольку числам t и t + 2nк соответствует одна и та же точка числовой окружности (чем мы не раз уже пользовались).<br>'''Свойство 3. '''Для любого значения t справедливы равенства: | + | [[Image:Alg37.jpg|480px|Решение]]<br> |
| | | | |
| - | [[Image:Alg318.jpg]]<br>Доказательство. Если числу t соответствует точка М числовой окружности, то числу t + n соответствует точка Р, симметричная точке М относительно центра окружности — начала координат (рис. 111). У таких точек абсциссы равны по модулю, но противоположны по знаку, и ординаты равны по модулю, но противоположны по знаку. Это значит, что
| + | <br>б)''' ''' В примере 16 из § 18 мы установили, что числу |
| | | | |
| - | [[Image:Alg319.jpg]]<br>'''2. '''Тангенс и котангенс.<br>'''Определение.''' Отношение синуса числа t к косинусу того же числа называют тангенсом числа t и обозначают Отношение косинуса числа t к синусу того же числа называют котангенсом числа t и обозначают | + | [[Image:Alg38.jpg|480px|Решение]] <br> |
| | | | |
| - | [[Image:Alg320.jpg]]<br>Впредь, говоря о t или t, мы будем подразумевать (не записывая), что аргумент t принимает только допустимые значения:
| + | <br>'''Пример 2.''' <br> |
| | | | |
| - | [[Image:Alg321.jpg]]<br>Опираясь на таблицу знаков синуса и косинуса по четвертям числовой окружности (она имеется в п. 1), нетрудно составить аналогичную таблицу для тангенса и котангенса: | + | Решить [[Рівняння з двома змінними та його розв'язок. Презентація уроку|уравнение]] [[Image:Alg39.jpg|Пример]]<br> |
| | | | |
| - | [[Image:Alg322.jpg]]<br>'''Пример 6.''' Вычислить:
| + | '''Решение.''' <br> |
| | | | |
| - | [[Image:Alg323.jpg]]<br>Как видите, зная значения синуса и косинуса числа I, нетрудно вычислить соответствующие значения тангенса и котангенса. Тем не менее есть смысл составить небольшую таблицу основных значений тангенса и котангенса:
| + | Учтем, что sin t — ордината точки М{<sub>1</sub>) числовой окружности. Значит, нам нужно найти на числовой окружности 1<br>точки с ординатой - и записать, каким числам I они соответствуют. Но эта задача уже решена выше — см. пример 2 из § 18: |
| | | | |
| - | [[Image:Alg324.jpg]]<br><br> | + | [[Image:Alg310.jpg|180px|Решение]]<br>'''Пример 3.''' <br> |
| | | | |
| - | А.Г. Мордкович Алгебра 9 класс | + | Решить уравнение [[Image:Alg311.jpg|Пример]]<br>'''Решение.''' <br> |
| | + | |
| | + | Учтем, что sin t — ордината точки М{<sub>1</sub>) числовой окружности. Значит, нам нужно найти на числовой окружности 1<br> точки с ординатой - и записать, каким числам I они соответствуют. Но эта задача уже решена выше — см. пример 3 из § 18: |
| | + | |
| | + | [[Image:Alg312.jpg|240px|Решение]]<br>'''Пример 4.''' <br> |
| | + | |
| | + | Решить уравнение: |
| | + | |
| | + | [[Image:Alg313.jpg|320px|Пример]]<br> |
| | + | |
| | + | '''Решение.'''<br> |
| | + | |
| | + | а)Нам нужно найти на числовой окружности точки с ординатой 0 и записать, каким числам I они соответствуют. Ординату 0 имеют [[Точка, пряма, площина. Промінь. Відрізок. Презентація уроку|точки]] А и С (рис. 109), они соответствуют числам 0 (точкаА), n (точка С), 2n (точка А), Зn (точка С), -n (точка С), -2k (точка А) и т.д. Короче это можно записать так: точки А и С соответствуют числам вида nk. |
| | + | |
| | + | [[Image:Alg314.jpg|320px|Решение]]<br> |
| | + | |
| | + | б) Ординату 1 имеет точка В числовой окружности (рис. 109). Значит, решения уравнения |
| | + | |
| | + | [[Image:Alg315.jpg|320px|Решение]]<br> |
| | + | |
| | + | '''Замечание.''' <br> |
| | + | |
| | + | Напомним еще раз о нашей договоренности: параметр k (или n) принимает любые целочисленные значения (k е n ), мы это постоянно подразумеваем, но, краткости ради, не записываем. Завершая разговор о синусе и [[Косинус угла. Полные уроки|косинусе]], остановимся на их свойствах.<br> |
| | + | |
| | + | '''Свойство 1.'''<br> |
| | + | |
| | + | Для любого значения I справедливы равенства: |
| | + | |
| | + | [[Image:Alg316.jpg|320px|Свойство]]<br> |
| | + | |
| | + | '''Доказательство'''. Если числу t соответствует точка М числовой окружности, то числу -1 соответствует точка Р, симметричная точке М относительно горизонтального диаметра [[Окружность и круг|окружности]] (рис. 110), т.е. симметричная точке М относительно оси абсцисс. У таких точек одна и та же абсцисса, а это значит, что сое (-t) = = соs t. У таких точек равные по модулю, но противоположные по знаку ординаты; это значит, что sin (-t) = cos t.<br> |
| | + | |
| | + | '''Свойство 2.''' <br> |
| | + | |
| | + | Для любого значения 1: справедливы равенства |
| | + | |
| | + | [[Image:Alg317.jpg|240px|Формула]]<br>Это очевидно, поскольку числам t и t + 2nк соответствует одна и та же точка числовой окружности (чем мы не раз уже пользовались).<br> |
| | + | |
| | + | '''Свойство 3. '''<br> |
| | + | |
| | + | Для любого значения t справедливы равенства: |
| | + | |
| | + | [[Image:Alg318.jpg|420px|Свойство]]<br>'''Доказательство'''. Если числу t соответствует точка М числовой окружности, то числу t + n соответствует точка Р, симметричная точке М относительно центра окружности — начала координат (рис. 111). У таких точек абсциссы равны по [[Задачі до теми «Модуль числа»|модулю]], но противоположны по знаку, и ординаты равны по модулю, но противоположны по знаку. Это значит, что |
| | + | |
| | + | [[Image:Alg319.jpg|480px|Окружности]]<br> |
| | + | |
| | + | <br>'''2. Тангенс и котангенс.'''<br> |
| | + | |
| | + | '''Определение.''' <br> |
| | + | |
| | + | Отношение синуса числа t к косинусу того же числа называют тангенсом числа t и обозначают Отношение косинуса числа t к синусу того же числа называют котангенсом числа t и обозначают |
| | + | |
| | + | [[Image:Alg320.jpg|480px|Тангенс и котангенс.]]<br> |
| | + | |
| | + | Впредь, говоря о t или t, мы будем подразумевать (не записывая), что аргумент t принимает только допустимые значения: |
| | + | |
| | + | [[Image:Alg321.jpg|320px|Тангенс и котангенс.]]<br>Опираясь на таблицу знаков синуса и косинуса по четвертям числовой окружности (она имеется в п. 1), нетрудно составить аналогичную таблицу для [[Значения синуса, косинуса и тангенса некоторых углов. Полные уроки|тангенса]] и котангенса: |
| | + | |
| | + | [[Image:Alg322.jpg|320px|Таблица]]<br> |
| | + | |
| | + | <br>'''Пример 6.''' <br> |
| | + | |
| | + | Вычислить: |
| | + | |
| | + | [[Image:Alg323.jpg|480px|Пример]]<br> |
| | + | |
| | + | Как видите, зная значения синуса и косинуса числа I, нетрудно вычислить соответствующие значения тангенса и котангенса. Тем не менее есть смысл составить небольшую таблицу основных значений тангенса и котангенса: |
| | + | |
| | + | [[Image:Alg324.jpg|240px|Таблица]]<br><br> |
| | + | |
| | + | ''А.Г. Мордкович [http://xvatit.com/vuzi/ Алгебра] 9 класс'' |
| | | | |
| | <br> | | <br> |
| Строка 58: |
Строка 128: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | | | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 18:46, 10 октября 2012
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Синус и косинус. Тангенс и котангенс
Синус и косинус. Тангенс и котангенс.
1. Синус и косинус.
Определение. Если точка М числовой окружности соответствует числу t, то абсциссу точки М называют косинусом числа t и обозначают соs t, а ординату точки М называют синусом числа t и обозначают sin t.
Итак (см.рис. 109),
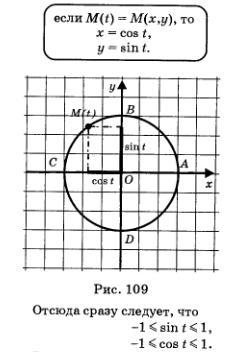
Вооружившись определением, вернемся к предыдущему параграфу и как бы заново перечитаем его.
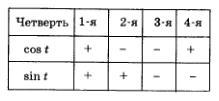
Мы отметили в § 18, что каждая точка числовой окружности имеет в системе хОу свои координаты, причем:
у точек первой четверти х > 0, у > 0;
у точек второй четверти х < 0, у > 0;
у точек третьей четверти х < 0, у < 0;
у точек четвертой четверти х > 0, у < 0 (рис. 104).
Это позволяет нам составить соответствующую таблицу знаков синуса и косинуса по четвертям числовой окружности:
Мы отметили в § 18, что уравнение числовой окружности имеет вид х2 + у2 = 1.
Тем самым фактически получено важное равенство, связывающее sin t и соs t:
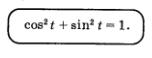
В § 18 было отмечено, как важно научиться отыскивать координаты точек числовой окружности, прежде всего тех, что представлены на первом и втором макетах (рис. 100 и 101). Теперь эта мысль стала, думается, предельно ясной: опираясь на таблицы 1 и 2 из § 18, мы без труда составим соответствующие таблицы для вычисления значений соs t и sin t.
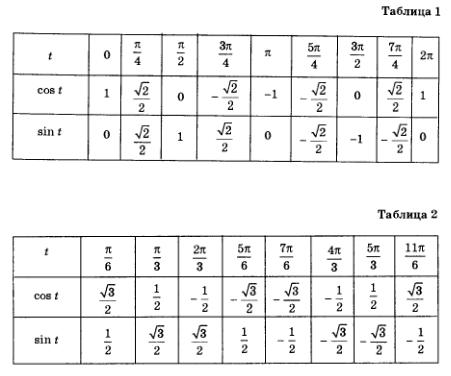
Пример 1.
Вычислить соs t и sin t, если:
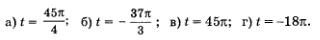
Решение:
а) В примере 1а из § 18 мы установили, что числу 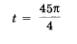 соответствует та же точка числовой окружности, что и соответствует та же точка числовой окружности, что и
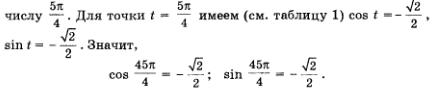
б) В примере 16 из § 18 мы установили, что числу
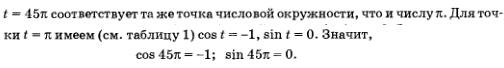
Пример 2.
Решить уравнение 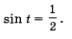
Решение.
Учтем, что sin t — ордината точки М{1) числовой окружности. Значит, нам нужно найти на числовой окружности 1
точки с ординатой - и записать, каким числам I они соответствуют. Но эта задача уже решена выше — см. пример 2 из § 18:
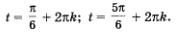
Пример 3.
Решить уравнение 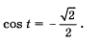
Решение.
Учтем, что sin t — ордината точки М{1) числовой окружности. Значит, нам нужно найти на числовой окружности 1
точки с ординатой - и записать, каким числам I они соответствуют. Но эта задача уже решена выше — см. пример 3 из § 18:
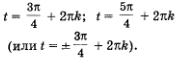
Пример 4.
Решить уравнение:
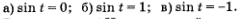
Решение.
а)Нам нужно найти на числовой окружности точки с ординатой 0 и записать, каким числам I они соответствуют. Ординату 0 имеют точки А и С (рис. 109), они соответствуют числам 0 (точкаА), n (точка С), 2n (точка А), Зn (точка С), -n (точка С), -2k (точка А) и т.д. Короче это можно записать так: точки А и С соответствуют числам вида nk.

б) Ординату 1 имеет точка В числовой окружности (рис. 109). Значит, решения уравнения
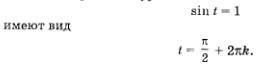
Замечание.
Напомним еще раз о нашей договоренности: параметр k (или n) принимает любые целочисленные значения (k е n ), мы это постоянно подразумеваем, но, краткости ради, не записываем. Завершая разговор о синусе и косинусе, остановимся на их свойствах.
Свойство 1.
Для любого значения I справедливы равенства:
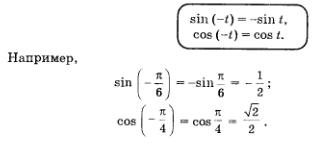
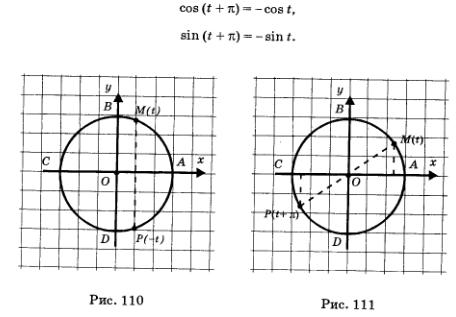
Доказательство. Если числу t соответствует точка М числовой окружности, то числу -1 соответствует точка Р, симметричная точке М относительно горизонтального диаметра окружности (рис. 110), т.е. симметричная точке М относительно оси абсцисс. У таких точек одна и та же абсцисса, а это значит, что сое (-t) = = соs t. У таких точек равные по модулю, но противоположные по знаку ординаты; это значит, что sin (-t) = cos t.
Свойство 2.
Для любого значения 1: справедливы равенства
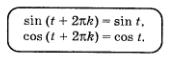
Это очевидно, поскольку числам t и t + 2nк соответствует одна и та же точка числовой окружности (чем мы не раз уже пользовались).
Свойство 3.
Для любого значения t справедливы равенства:
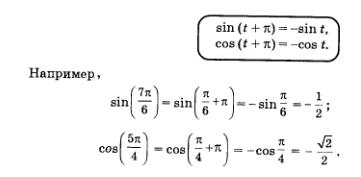
Доказательство. Если числу t соответствует точка М числовой окружности, то числу t + n соответствует точка Р, симметричная точке М относительно центра окружности — начала координат (рис. 111). У таких точек абсциссы равны по модулю, но противоположны по знаку, и ординаты равны по модулю, но противоположны по знаку. Это значит, что
2. Тангенс и котангенс.
Определение.
Отношение синуса числа t к косинусу того же числа называют тангенсом числа t и обозначают Отношение косинуса числа t к синусу того же числа называют котангенсом числа t и обозначают
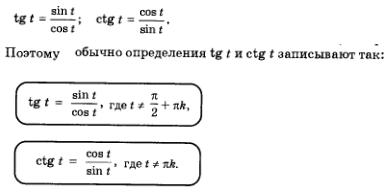
Впредь, говоря о t или t, мы будем подразумевать (не записывая), что аргумент t принимает только допустимые значения:
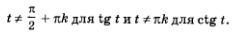
Опираясь на таблицу знаков синуса и косинуса по четвертям числовой окружности (она имеется в п. 1), нетрудно составить аналогичную таблицу для тангенса и котангенса:
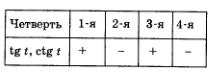
Пример 6.
Вычислить:
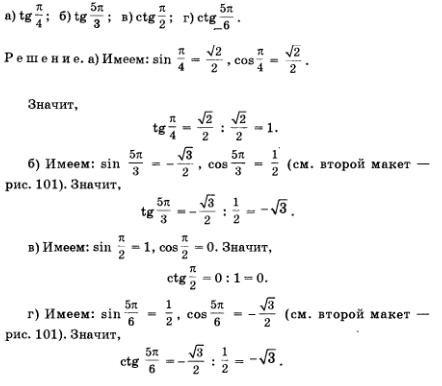
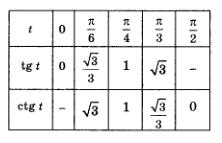
Как видите, зная значения синуса и косинуса числа I, нетрудно вычислить соответствующие значения тангенса и котангенса. Тем не менее есть смысл составить небольшую таблицу основных значений тангенса и котангенса:
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|