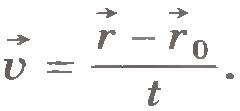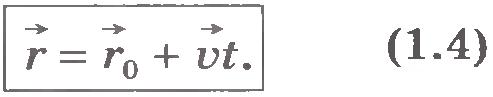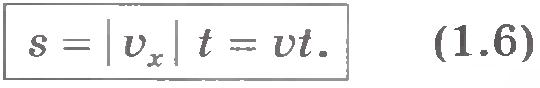|
|
|
| Строка 1: |
Строка 1: |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Физика и астрономия|Физика и астрономия]]>>[[Физика 10 класс|Физика 10 класс]]>>Физика: Уравнение равномерного прямолинейного движения ''' <br> | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Физика и астрономия|Физика и астрономия]]>>[[Физика 10 класс|Физика 10 класс]]>>Физика: Уравнение равномерного прямолинейного движения ''' <br> |
| | | | |
| - | <br> | + | <br> |
| | | | |
| | <metakeywords>Физика, 10 класс, Уравнение равномерного, прямолинейного движения</metakeywords><br> | | <metakeywords>Физика, 10 класс, Уравнение равномерного, прямолинейного движения</metakeywords><br> |
| | | | |
| - | Получим уравнение равномерного прямолинейного движения точки. Для этого воспользуемся определением скорости.<br> Пусть радиус-вектор [[Image:a8-6.jpg]] задает положение точки в начальный момент времени ''t<sub>0</sub>'', а радиус-вектор [[Image:a4-2.jpg]] - в момент времени ''t''. Тогда [[Image:a8-7.jpg]], [[Image:a8-8.jpg]], и выражение для скорости принимает вид [[Image:a8-1.jpg]].<br> Если начальный момент времени ''t<sub>0</sub>'' принять равным нулю, то<br>[[Image:a8-2.jpg|center]]Отсюда<br>[[Image:a8-3.jpg|center]] Последнее уравнение и есть уравнение равномерного прямолинейного движения точки, записанное в векторной форме. Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий ее положение в начальный момент времени.<br> Вместо векторного уравнения (1.4) можно записать три эквивалентных ему уравнения в проекциях на оси координат. Радиус-вектор [[Image:a4-2.jpg]] является суммой двух векторов: радиус-вектора [[Image:a8-6.jpg]] и вектора [[Image:a8-9.jpg]]. Следовательно, проекции радиус-вектора [[Image:a4-2.jpg]] на оси координат должны быть равны сумме проекций этих двух векторов на те же оси.<br> Выберем оси координат так, чтобы тело двигалось по какой-либо оси, например по оси ''ОХ''. Тогда векторы [[Image:a8-6.jpg]] и [[Image:a7-3.jpg]] будут составлять с осями ''ОY'' и ''ОZ'', прямой угол. Поэтому их проекции на эти оси равны нулю. А значит, равны нулю в любой момент времени и проекции радиус-вектора [[Image:a4-2.jpg]] на оси ''ОY'' и ''ОZ''. Так как проекции радиус-вектора на координатные оси равны координатам его конца, то ''r<sub>x</sub>=x'' и''r<sub>0x</sub>=x<sub>0</sub>''. Поэтому в проекциях на ось ''ОХ ''уравнение (1.4) можно записать в виде<br>[[Image:a8-4.jpg|center]] Уравнение (1.5) есть уравнение равномерного прямоли¬нейного движения точки, записанное в координатной фор¬ме. Оно позволяет найти координату х тела при этом движении в любой момент времени, если известны проекция его скоро¬сти на ось ОX и его начальная ко¬ордината х0.<br>Путь s, пройденный точкой при движении вдоль оси ОХ (рис. 1.13), равен модулю изменения ее координаты: *****. Его можно най¬ти, зная модуль скорости *****:<br><br>Отметим, что, строго говоря, равномерного прямоли¬нейного движения не существует. Автомобиль на шоссе никогда не едет абсолютно прямо, небольшие отклонения в ту или иную сторону от прямой всегда имеются. И значе¬ние скорости слегка изменяется. Незначительная неров¬ность шоссе, порыв ветра, чуть-чуть большее нажатие на педаль газа и другие причины вызывают небольшие изме¬нения скорости. Но приближенно на протяжении не слиш¬ком большого промежутка времени движение автомобиля можно считать равномерным и прямолинейным с доста¬точной для практических целей точностью. Таково одно из упрощений действительности, позволяющее без боль¬ших усилий описывать многие движения.<br>Графическое представление равномерного прямолиней¬ного движения. Полученные результаты можно изобразить наглядно с помощью графиков. Особенно прост график за¬висимости проекции скорости от времени (рис. 1.14). Это прямая, параллельная оси времени. Пло¬щадь прямоугольника ОАВС, за¬штрихованная на рисунке, равна изменению координаты точки за время t. Ведь сторона ОА есть vх, а сторона ОС - время движения t, поэтому *****.<br>На рисунке 1.15 приведены примеры графиков зависимости координаты от времени для трех различных случаев равномерного прямолинейного движения. Пря¬мая 1 соответствует случаю х0 = 0, vх1 > 0; прямая 2 - случаю х0 < 0, vх2 > 0, а прямая 3 - случаю х0 > 0, vх3 < 0. Угол наклона α2 прямой 2 больше, чем угол накло¬на α1 прямой 1. За один и тот же промежуток времени t1 точка, движущаяся со скоростью vх2, проходит большее расстояние, чем при движении ее со скоростью vх1. Во втором случае скорость vх больше, чем в первом. Скорость определяет угол наклона прямой к оси t. Очевидно, скорость vх числен¬но равна тангенсу угла а. В случае 3 α3 < 0, движение про¬исходит в сторону, противоположную оси ОХ.<br>Получено уравнение прямолинейного равномерного движения точки. Графики зависимости vх (t) и х (t) позво¬ляют легко проанализировать и сравнить движения.<br><br><br>???<br>1. Как записывается в векторной форме уравнение равномер¬ного прямолинейного движения точки?<br>2. Как записывается в координатной форме уравнение равно¬мерного прямолинейного движения точки, если она движется: по оси ОУ? по оси ОZ?<br> | + | Получим уравнение равномерного прямолинейного движения точки. Для этого воспользуемся определением скорости.<br> Пусть радиус-вектор [[Image:A8-6.jpg]] задает положение точки в начальный момент времени ''t<sub>0</sub>'', а радиус-вектор [[Image:A4-2.jpg]] - в момент времени ''t''. Тогда [[Image:A8-7.jpg]], [[Image:A8-8.jpg]], и выражение для скорости принимает вид [[Image:A8-1.jpg]].<br> Если начальный момент времени ''t<sub>0</sub>'' принять равным нулю, то<br>[[Image:A8-2.jpg|center]]Отсюда<br>[[Image:A8-3.jpg|center]] Последнее уравнение и есть уравнение равномерного прямолинейного движения точки, записанное в векторной форме. Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий ее положение в начальный момент времени.<br> Вместо векторного уравнения (1.4) можно записать три эквивалентных ему уравнения в проекциях на оси координат. Радиус-вектор [[Image:A4-2.jpg]] является суммой двух векторов: радиус-вектора [[Image:A8-6.jpg]] и вектора [[Image:A8-9.jpg]]. Следовательно, проекции радиус-вектора [[Image:A4-2.jpg]] на оси координат должны быть равны сумме проекций этих двух векторов на те же оси.<br> Выберем оси координат так, чтобы тело двигалось по какой-либо оси, например по оси ''ОХ''. Тогда векторы [[Image:A8-6.jpg]] и [[Image:A7-3.jpg]] будут составлять с осями ''ОY'' и ''ОZ'', прямой угол. Поэтому их проекции на эти оси равны нулю. А значит, равны нулю в любой момент времени и проекции радиус-вектора [[Image:A4-2.jpg]] на оси ''ОY'' и ''ОZ''. Так как проекции радиус-вектора на координатные оси равны координатам его конца, то ''r<sub>x</sub>=x'' и''r<sub>0x</sub>=x<sub>0</sub>''. Поэтому в проекциях на ось ''ОХ ''уравнение (1.4) можно записать в виде<br>[[Image:A8-4.jpg|center]] Уравнение (1.5) есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме. Оно позволяет найти координату ''х'' тела при этом движении в любой момент времени, если известны проекция его скорости на ось ''ОX'' и его начальная координата ''х<sub>0</sub>''.<br> Путь ''s'', пройденный точкой при движении вдоль оси ''ОХ ''(''рис.1.13''), равен модулю изменения ее координаты: [[Image:a8-10.jpg]]. Его можно найти, зная модуль скорости [[Image:a8-11.jpg]]:<br>[[Image:a8-5.jpg|center]][[Image:a1.13.jpg|center]] Отметим, что, строго говоря, равномерного прямолинейного движения не существует. Автомобиль на шоссе никогда не едет абсолютно прямо, небольшие отклонения в ту или иную сторону от прямой всегда имеются. И значение скорости слегка изменяется. Незначительная неровность шоссе, порыв ветра, чуть-чуть большее нажатие на педаль газа и другие причины вызывают небольшие изменения скорости. Но приближенно на протяжении не слишком большого промежутка времени движение автомобиля можно считать равномерным и прямолинейным с достаточной для практических целей точностью. Таково одно из упрощений действительности, позволяющее без больших усилий описывать многие движения.<br> '''Графическое представление равномерного прямолинейного движения'''. Полученные результаты можно изобразить наглядно с помощью графиков. Особенно прост график зависимости проекции скорости от времени (''рис.1.14''). Это прямая, параллельная оси времени. Площадь прямоугольника ''ОАВС'', заштрихованная на рисунке, равна изменению координаты точки за время ''t''. Ведь сторона ''ОА'' есть [[Image:a13-16.jpg]], а сторона ''ОС'' - время движения ''t'', поэтому [[Image:a8-12.jpg]]. |
| - | <br> | + | |
| | + | [[Image:a1.14.jpg|center]] На рисунке 1.15 приведены примеры графиков зависимости координаты от времени для трех различных случаев равномерного прямолинейного движения. Прямая ''1'' соответствует случаю ''х<sub>0</sub> = 0'', ''v<sub>х1</sub> > 0''; прямая ''2'' - случаю ''х<sub>0</sub> < 0'', ''v<sub>х2</sub> > 0'', а прямая ''3'' - случаю ''х<sub>0</sub> > 0'', ''v<sub>х3</sub> < 0''. Угол наклона ''α<sub>2</sub>'' прямой ''2'' больше, чем угол наклона ''α<sub>1</sub> ''прямой ''1''. За один и тот же промежуток времени ''t<sub>1</sub>'' точка, движущаяся со скоростью''v<sub>х2</sub>'', проходит большее расстояние, чем при движении ее со скоростью ''v<sub>х1</sub>''. Во втором случае скорость ''v<sub>х</sub>'' больше, чем в первом. Скорость определяет угол наклона прямой к оси ''t''. Очевидно, скорость ''v<sub>х</sub>'' численно равна тангенсу угла ''α''. В случае ''3 α<sub>3</sub> < 0'', движение происходит в сторону, противоположную оси ''ОХ''. |
| | + | |
| | + | [[Image:a1.15.jpg|center]] Получено уравнение прямолинейного равномерного движения точки. Графики зависимости''v<sub>х</sub>(t)'' и ''х(t)'' позволяют легко проанализировать и сравнить движения.<br><br><br> ???<br> 1. Как записывается в векторной форме уравнение равномерного прямолинейного движения точки?<br> 2. Как записывается в координатной форме уравнение равномерного прямолинейного движения точки, если она движется: по оси ''ОY''? по оси ''ОZ''?<br> <br> |
| | | | |
| | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' | | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' |
Версия 19:56, 2 августа 2010
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Уравнение равномерного прямолинейного движения
Получим уравнение равномерного прямолинейного движения точки. Для этого воспользуемся определением скорости.
Пусть радиус-вектор 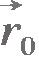 задает положение точки в начальный момент времени t0, а радиус-вектор задает положение точки в начальный момент времени t0, а радиус-вектор 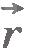 - в момент времени t. Тогда - в момент времени t. Тогда 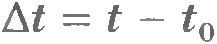 , , 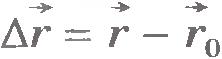 , и выражение для скорости принимает вид , и выражение для скорости принимает вид 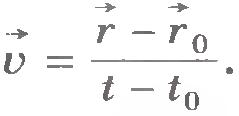 . .
Если начальный момент времени t0 принять равным нулю, то
Отсюда
Последнее уравнение и есть уравнение равномерного прямолинейного движения точки, записанное в векторной форме. Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий ее положение в начальный момент времени.
Вместо векторного уравнения (1.4) можно записать три эквивалентных ему уравнения в проекциях на оси координат. Радиус-вектор 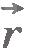 является суммой двух векторов: радиус-вектора является суммой двух векторов: радиус-вектора 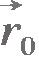 и вектора и вектора 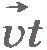 . Следовательно, проекции радиус-вектора . Следовательно, проекции радиус-вектора 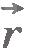 на оси координат должны быть равны сумме проекций этих двух векторов на те же оси. на оси координат должны быть равны сумме проекций этих двух векторов на те же оси.
Выберем оси координат так, чтобы тело двигалось по какой-либо оси, например по оси ОХ. Тогда векторы 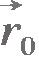 и и 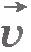 будут составлять с осями ОY и ОZ, прямой угол. Поэтому их проекции на эти оси равны нулю. А значит, равны нулю в любой момент времени и проекции радиус-вектора будут составлять с осями ОY и ОZ, прямой угол. Поэтому их проекции на эти оси равны нулю. А значит, равны нулю в любой момент времени и проекции радиус-вектора 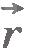 на оси ОY и ОZ. Так как проекции радиус-вектора на координатные оси равны координатам его конца, то rx=x иr0x=x0. Поэтому в проекциях на ось ОХ уравнение (1.4) можно записать в виде на оси ОY и ОZ. Так как проекции радиус-вектора на координатные оси равны координатам его конца, то rx=x иr0x=x0. Поэтому в проекциях на ось ОХ уравнение (1.4) можно записать в виде
Уравнение (1.5) есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме. Оно позволяет найти координату х тела при этом движении в любой момент времени, если известны проекция его скорости на ось ОX и его начальная координата х0.
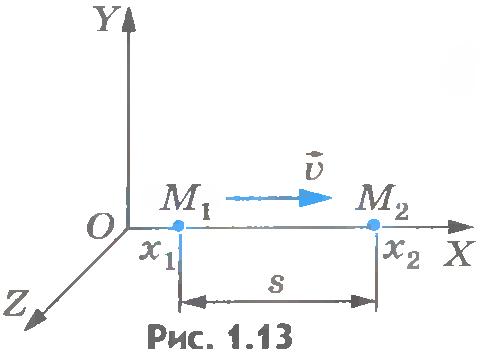
Путь s, пройденный точкой при движении вдоль оси ОХ (рис.1.13), равен модулю изменения ее координаты: 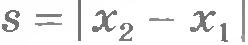 . Его можно найти, зная модуль скорости . Его можно найти, зная модуль скорости  : :
Отметим, что, строго говоря, равномерного прямолинейного движения не существует. Автомобиль на шоссе никогда не едет абсолютно прямо, небольшие отклонения в ту или иную сторону от прямой всегда имеются. И значение скорости слегка изменяется. Незначительная неровность шоссе, порыв ветра, чуть-чуть большее нажатие на педаль газа и другие причины вызывают небольшие изменения скорости. Но приближенно на протяжении не слишком большого промежутка времени движение автомобиля можно считать равномерным и прямолинейным с достаточной для практических целей точностью. Таково одно из упрощений действительности, позволяющее без больших усилий описывать многие движения.
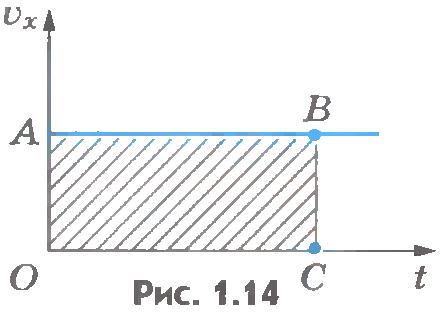
Графическое представление равномерного прямолинейного движения. Полученные результаты можно изобразить наглядно с помощью графиков. Особенно прост график зависимости проекции скорости от времени (рис.1.14). Это прямая, параллельная оси времени. Площадь прямоугольника ОАВС, заштрихованная на рисунке, равна изменению координаты точки за время t. Ведь сторона ОА есть 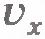 , а сторона ОС - время движения t, поэтому , а сторона ОС - время движения t, поэтому  .
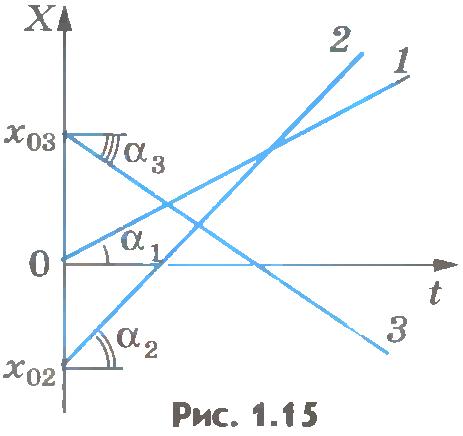
На рисунке 1.15 приведены примеры графиков зависимости координаты от времени для трех различных случаев равномерного прямолинейного движения. Прямая 1 соответствует случаю х0 = 0, vх1 > 0; прямая 2 - случаю х0 < 0, vх2 > 0, а прямая 3 - случаю х0 > 0, vх3 < 0. Угол наклона α2 прямой 2 больше, чем угол наклона α1 прямой 1. За один и тот же промежуток времени t1 точка, движущаяся со скоростьюvх2, проходит большее расстояние, чем при движении ее со скоростью vх1. Во втором случае скорость vх больше, чем в первом. Скорость определяет угол наклона прямой к оси t. Очевидно, скорость vх численно равна тангенсу угла α. В случае 3 α3 < 0, движение происходит в сторону, противоположную оси ОХ.
Получено уравнение прямолинейного равномерного движения точки. Графики зависимостиvх(t) и х(t) позволяют легко проанализировать и сравнить движения. .
На рисунке 1.15 приведены примеры графиков зависимости координаты от времени для трех различных случаев равномерного прямолинейного движения. Прямая 1 соответствует случаю х0 = 0, vх1 > 0; прямая 2 - случаю х0 < 0, vх2 > 0, а прямая 3 - случаю х0 > 0, vх3 < 0. Угол наклона α2 прямой 2 больше, чем угол наклона α1 прямой 1. За один и тот же промежуток времени t1 точка, движущаяся со скоростьюvх2, проходит большее расстояние, чем при движении ее со скоростью vх1. Во втором случае скорость vх больше, чем в первом. Скорость определяет угол наклона прямой к оси t. Очевидно, скорость vх численно равна тангенсу угла α. В случае 3 α3 < 0, движение происходит в сторону, противоположную оси ОХ.
Получено уравнение прямолинейного равномерного движения точки. Графики зависимостиvх(t) и х(t) позволяют легко проанализировать и сравнить движения.
???
1. Как записывается в векторной форме уравнение равномерного прямолинейного движения точки?
2. Как записывается в координатной форме уравнение равномерного прямолинейного движения точки, если она движется: по оси ОY? по оси ОZ?
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Планирования по физике, учебники и книги онлайн, курсы и задания по физике для 10 класса
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|
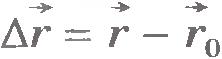 , и выражение для скорости принимает вид
, и выражение для скорости принимает вид 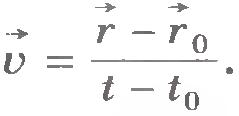 .
.