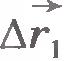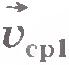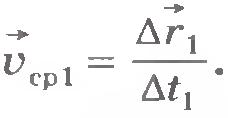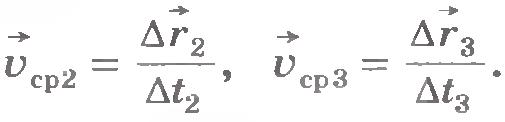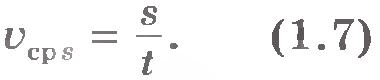|
|
|
| Строка 5: |
Строка 5: |
| | <metakeywords>Физика, 10 класс, Мгновенная скорость</metakeywords> | | <metakeywords>Физика, 10 класс, Мгновенная скорость</metakeywords> |
| | | | |
| - | Ни одно тело не движется все время с постоянной скоростью. Трогаясь с места, автомобиль начинает двигаться все быстрее и быстрее. Некоторое время он может двигаться равномерно или почти равномерно, но рано или поздно замедляет движение и останавливается. При этом он проходит различные расстояния за одни и те же интервалы времени, т. е. движется неравномерно.<br> Неравномерное движение может быть как прямолинейным, так и криволинейным.<br> Чтобы полностью описать неравномерное движение точки, надо знать ее положение и скорость в каждый момент времени. Скорость в данный момент времени называется мгновенной скоростью. <br> Что же понимают под мгновенной скоростью? <br> Пусть точка, двигаясь неравномерно и криволинейно, в некоторый момент времени ''t'' занимает положение ''М'' (''рис.1.18''). По прошествии времени [[Image:A9-4.jpg]] от этого момента точка займет положение ''М<sub>1</sub>'', совершив перемещение [[Image:A9-5.jpg]]. Поделив вектор [[Image:A9-5.jpg]], на промежуток времени [[Image:A9-4.jpg]], найдем скорость такого равномерного прямолинейного движения, с которой должна была бы двигаться точка, чтобы за время [[Image:A6-5.jpg]] попасть из положения ''М'' в положение ''М<sub>1</sub>''. Эту скорость называют '''средней''' скоростью перемещения точки за время [[Image:A9-4.jpg]]. Обозначив ее через [[Image:a9-7.jpg]][[Image:A9-7.jpg]], запишем: [[Image:a9-1.jpg]][[Image:A9-1.jpg]]. | + | Ни одно тело не движется все время с постоянной скоростью. Трогаясь с места, автомобиль начинает двигаться все быстрее и быстрее. Некоторое время он может двигаться равномерно или почти равномерно, но рано или поздно замедляет движение и останавливается. При этом он проходит различные расстояния за одни и те же интервалы времени, т. е. движется неравномерно.<br> Неравномерное движение может быть как прямолинейным, так и криволинейным.<br> Чтобы полностью описать неравномерное движение точки, надо знать ее положение и скорость в каждый момент времени. Скорость в данный момент времени называется мгновенной скоростью. <br> Что же понимают под мгновенной скоростью? <br> Пусть точка, двигаясь неравномерно и криволинейно, в некоторый момент времени ''t'' занимает положение ''М'' (''рис.1.18''). По прошествии времени [[Image:A9-4.jpg]] от этого момента точка займет положение ''М<sub>1</sub>'', совершив перемещение [[Image:A9-5.jpg]]. Поделив вектор [[Image:A9-5.jpg]], на промежуток времени [[Image:A9-4.jpg]], найдем скорость такого равномерного прямолинейного движения, с которой должна была бы двигаться точка, чтобы за время [[Image:A6-5.jpg]] попасть из положения ''М'' в положение ''М<sub>1</sub>''. Эту скорость называют '''средней''' скоростью перемещения точки за время [[Image:A9-4.jpg]]. Обозначив ее через[[Image:A9-7.jpg]][[Image:A9-7.jpg]], запишем:[[Image:A9-1.jpg]][[Image:A9-1.jpg]]. |
| | | | |
| - | [[Image:a1.18.jpg|center]] Найдем средние скорости за все меньшие и меньшие промежутки времени: | + | [[Image:A1.18.jpg|center]] Найдем средние скорости за все меньшие и меньшие промежутки времени: |
| | | | |
| | [[Image:A9-2.jpg|center]] При уменьшении промежутка времени [[Image:A6-5.jpg]] перемещения точки уменьшаются по модулю и меняются по направлению. Соответственно этому, средние скорости также меняются как по модулю так и направлению. Но по мере приближения промежутка времени [[Image:A6-5.jpg]] к нулю средние скорости все меньше и меньше будут отличаться друг от друга. А это означает, что при стремлении промежутка времени [[Image:A6-5.jpg]] к нулю отношение [[Image:A9-8.jpg]] стремится к определенному вектору как к своему предельному значению. В механике такую величину называют скоростью точки в данный момент времени, или просто мгновенной скоростью, и обозначают [[Image:A7-3.jpg]].<br> '''Мгновенная скорость точки''' есть величина, равная пределу отношения перемещения [[Image:A6-6.jpg]] к промежутку времени [[Image:A6-5.jpg]], в течение которого это перемещение произошло, при стремлении промежутка [[Image:A6-5.jpg]] к нулю.<br> Выясним теперь, как направлен вектор мгновенной скорости. В любой точке траектории вектор мгновенной скорости направлен так, как в пределе, при стремлении промежутка времени [[Image:A6-5.jpg]] к нулю, направлена средняя скорость перемещения. Эта средняя скорость направлена так, как направлен вектор перемещения [[Image:A6-6.jpg]]. Из рисунка 1.18 видно, что при уменьшении промежутка времени [[Image:A6-5.jpg]] вектор [[Image:A6-6.jpg]], уменьшая свою длину, одновременно поворачивается. Чем короче становится вектор [[Image:A6-6.jpg]], тем ближе он к касательной, проведенной к траектории в данной точке ''М''. | | [[Image:A9-2.jpg|center]] При уменьшении промежутка времени [[Image:A6-5.jpg]] перемещения точки уменьшаются по модулю и меняются по направлению. Соответственно этому, средние скорости также меняются как по модулю так и направлению. Но по мере приближения промежутка времени [[Image:A6-5.jpg]] к нулю средние скорости все меньше и меньше будут отличаться друг от друга. А это означает, что при стремлении промежутка времени [[Image:A6-5.jpg]] к нулю отношение [[Image:A9-8.jpg]] стремится к определенному вектору как к своему предельному значению. В механике такую величину называют скоростью точки в данный момент времени, или просто мгновенной скоростью, и обозначают [[Image:A7-3.jpg]].<br> '''Мгновенная скорость точки''' есть величина, равная пределу отношения перемещения [[Image:A6-6.jpg]] к промежутку времени [[Image:A6-5.jpg]], в течение которого это перемещение произошло, при стремлении промежутка [[Image:A6-5.jpg]] к нулю.<br> Выясним теперь, как направлен вектор мгновенной скорости. В любой точке траектории вектор мгновенной скорости направлен так, как в пределе, при стремлении промежутка времени [[Image:A6-5.jpg]] к нулю, направлена средняя скорость перемещения. Эта средняя скорость направлена так, как направлен вектор перемещения [[Image:A6-6.jpg]]. Из рисунка 1.18 видно, что при уменьшении промежутка времени [[Image:A6-5.jpg]] вектор [[Image:A6-6.jpg]], уменьшая свою длину, одновременно поворачивается. Чем короче становится вектор [[Image:A6-6.jpg]], тем ближе он к касательной, проведенной к траектории в данной точке ''М''. |
Версия 20:55, 2 августа 2010
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Мгновенная скорость
Ни одно тело не движется все время с постоянной скоростью. Трогаясь с места, автомобиль начинает двигаться все быстрее и быстрее. Некоторое время он может двигаться равномерно или почти равномерно, но рано или поздно замедляет движение и останавливается. При этом он проходит различные расстояния за одни и те же интервалы времени, т. е. движется неравномерно.
Неравномерное движение может быть как прямолинейным, так и криволинейным.
Чтобы полностью описать неравномерное движение точки, надо знать ее положение и скорость в каждый момент времени. Скорость в данный момент времени называется мгновенной скоростью.
Что же понимают под мгновенной скоростью?
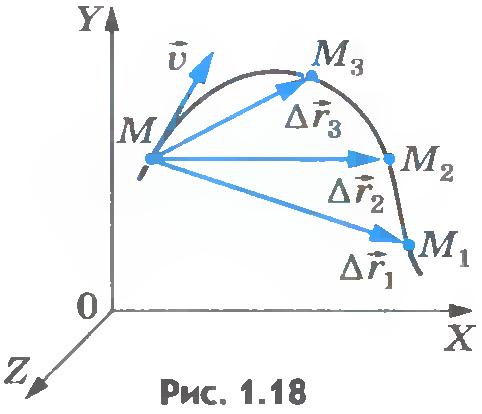
Пусть точка, двигаясь неравномерно и криволинейно, в некоторый момент времени t занимает положение М (рис.1.18). По прошествии времени 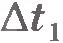 от этого момента точка займет положение М1, совершив перемещение от этого момента точка займет положение М1, совершив перемещение 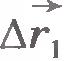 . Поделив вектор . Поделив вектор 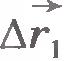 , на промежуток времени , на промежуток времени 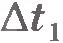 , найдем скорость такого равномерного прямолинейного движения, с которой должна была бы двигаться точка, чтобы за время , найдем скорость такого равномерного прямолинейного движения, с которой должна была бы двигаться точка, чтобы за время  попасть из положения М в положение М1. Эту скорость называют средней скоростью перемещения точки за время попасть из положения М в положение М1. Эту скорость называют средней скоростью перемещения точки за время 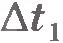 . Обозначив ее через . Обозначив ее через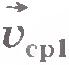 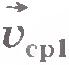 , запишем: , запишем: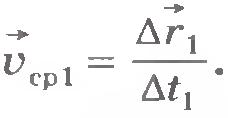 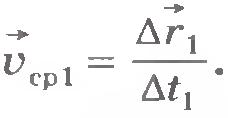 . .
Найдем средние скорости за все меньшие и меньшие промежутки времени:
При уменьшении промежутка времени  перемещения точки уменьшаются по модулю и меняются по направлению. Соответственно этому, средние скорости также меняются как по модулю так и направлению. Но по мере приближения промежутка времени перемещения точки уменьшаются по модулю и меняются по направлению. Соответственно этому, средние скорости также меняются как по модулю так и направлению. Но по мере приближения промежутка времени  к нулю средние скорости все меньше и меньше будут отличаться друг от друга. А это означает, что при стремлении промежутка времени к нулю средние скорости все меньше и меньше будут отличаться друг от друга. А это означает, что при стремлении промежутка времени  к нулю отношение к нулю отношение 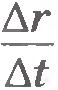 стремится к определенному вектору как к своему предельному значению. В механике такую величину называют скоростью точки в данный момент времени, или просто мгновенной скоростью, и обозначают стремится к определенному вектору как к своему предельному значению. В механике такую величину называют скоростью точки в данный момент времени, или просто мгновенной скоростью, и обозначают 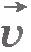 . .
Мгновенная скорость точки есть величина, равная пределу отношения перемещения 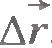 к промежутку времени к промежутку времени  , в течение которого это перемещение произошло, при стремлении промежутка , в течение которого это перемещение произошло, при стремлении промежутка  к нулю. к нулю.
Выясним теперь, как направлен вектор мгновенной скорости. В любой точке траектории вектор мгновенной скорости направлен так, как в пределе, при стремлении промежутка времени  к нулю, направлена средняя скорость перемещения. Эта средняя скорость направлена так, как направлен вектор перемещения к нулю, направлена средняя скорость перемещения. Эта средняя скорость направлена так, как направлен вектор перемещения 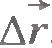 . Из рисунка 1.18 видно, что при уменьшении промежутка времени . Из рисунка 1.18 видно, что при уменьшении промежутка времени  вектор вектор 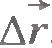 , уменьшая свою длину, одновременно поворачивается. Чем короче становится вектор , уменьшая свою длину, одновременно поворачивается. Чем короче становится вектор 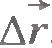 , тем ближе он к касательной, проведенной к траектории в данной точке М.
Следовательно, мгновенная скорость направлена по касательной к траектории (см. рис.1.18). , тем ближе он к касательной, проведенной к траектории в данной точке М.
Следовательно, мгновенная скорость направлена по касательной к траектории (см. рис.1.18).
В частности, скорость точки, движущейся по окружности, направлена по касательной к этой окружности. В этом нетрудно убедиться. Если маленькие частички отделяются от вращающегося диска, то они летят по касательной, так как имеют в момент отрыва скорость, равную скорости точек на окружности диска. Вот почему грязь из-под колес буксующей автомашины летит по касательной к окружности колес (рис.1.19).
Помимо средней скорости перемещения, для описания движения чаще пользуются средней путевой скоростью 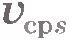 . Эта средняя скорость определяется отношением пути к промежутку времени, за который этот путь пройден: . Эта средняя скорость определяется отношением пути к промежутку времени, за который этот путь пройден:
Когда мы говорим, что путь от Москвы до Санкт-Петербурга поезд прошел со скоростью 80 км/ч, мы имеем в виду именно среднюю путевую скорость движения поезда между этими городами. Модуль средней скорости перемещения при этом будет меньше средней путевой скорости, так как  . .
Понятие мгновенной скорости - одно из основных понятий кинематики. Это понятие относится к точке. Поэтому в дальнейшем, говоря о скорости движения тела, которое нельзя считать точкой, мы можем говорить о скорости какой-нибудь его точки.
???
1. Что называется средней скоростью перемещения?
2. Что такое мгновенная скорость?
3. Как направлена мгновенная скорость в данной точке траектории?
4. Точка движется по криволинейной траектории так, что модуль ее скорости не изменяется. Означает ли это, что скорость точки постоянна?
5. Что такое средняя путевая скорость?
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Планирования по физике, учебники и книги онлайн, курсы и задания по физике для 10 класса
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|
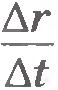 стремится к определенному вектору как к своему предельному значению. В механике такую величину называют скоростью точки в данный момент времени, или просто мгновенной скоростью, и обозначают
стремится к определенному вектору как к своему предельному значению. В механике такую величину называют скоростью точки в данный момент времени, или просто мгновенной скоростью, и обозначают  .
.