|
|
| Строка 5: |
Строка 5: |
| | <metakeywords>Физика, 10 класс, Сложение скоростей</metakeywords> | | <metakeywords>Физика, 10 класс, Сложение скоростей</metakeywords> |
| | | | |
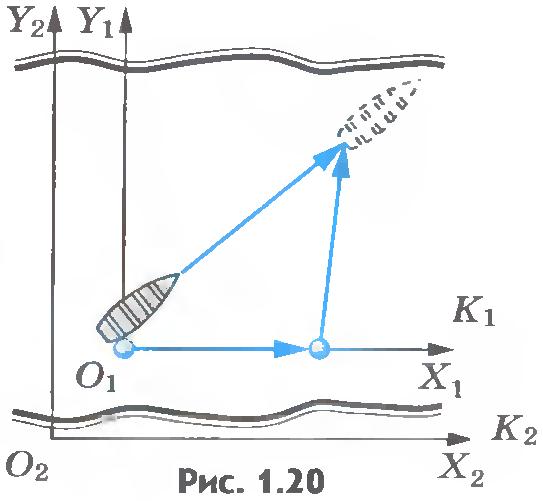
| - | Пусть по реке плывет моторная лодка и нам известна ее скорость [[Image:A10-5.jpg|19x29px]], относительно воды, точнее, относительно системы отсчета ''К<sub>1</sub>'', движущейся вместе с водой.<br> Такую систему отсчета можно связать, например, с мячом, выпавшим из лодки и плывущим по течению. Если известна еще и скорость течения реки [[Image:A10-6.jpg|15x25px]] относительно системы отсчета ''К<sub>2</sub>'', связанной с берегом, т. е. скорость системы отсчета''К<sub>1</sub>'' относительно системы отсчета ''К<sub>2</sub>'', то можно определить скорость лодки [[Image:A10-7.jpg|20x28px]] относительно берега (''рис.1.20''). | + | Пусть по реке плывет моторная лодка и нам известна ее скорость [[Image:A10-5.jpg|19x29px|A10-5.jpg]], относительно [[Тема_46._Вода_у_небезпеці|воды]], точнее, относительно системы отсчета ''К<sub>1</sub>'', движущейся вместе с водой.<br> Такую систему отсчета можно связать, например, с мячом, выпавшим из лодки и плывущим по течению. Если известна еще и скорость течения реки [[Image:A10-6.jpg|15x25px|A10-6.jpg]] относительно системы отсчета ''К<sub>2</sub>'', связанной с берегом, т. е. скорость системы отсчета''К<sub>1</sub>'' относительно системы отсчета ''К<sub>2</sub>'', то можно определить скорость лодки [[Image:A10-7.jpg|20x28px|A10-7.jpg]] относительно берега (''рис.1.20''). |
| | | | |
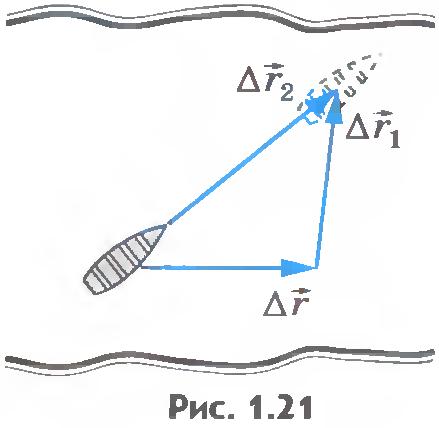
| - | [[Image:A1.20.jpg|center|227x214px]] За промежуток времени [[Image:A10-8.jpg|24x17px]] перемещения лодки и мяча относительно берега равны [[Image:A10-9.jpg|26x23px]] и [[Image:A10-10.jpg|25x21px]] (''рис.1.20''), а перемещение лодки относительно мяча равно [[Image:A10-11.jpg|28x26px]]. Из рисунка 1.21 видно, что <br> | + | [[Image:A1.20.jpg|center|227x214px|Сложение скоростей]] За промежуток времени [[Image:A10-8.jpg|24x17px|A10-8.jpg]] перемещения лодки и мяча относительно берега равны [[Image:A10-9.jpg|26x23px|A10-9.jpg]] и [[Image:A10-10.jpg|25x21px|A10-10.jpg]] (''рис.1.20''), а перемещение лодки относительно мяча равно [[Image:A10-11.jpg|28x26px|A10-11.jpg]]. Из рисунка 1.21 видно, что <br> |
| | | | |
| - | [[Image:A10-1.jpg|center|215x30px]][[Image:A1.21.jpg|center|175x171px]] Разделив левую и правую части уравнения (1.8) на [[Image:A10-8.jpg|22x16px]], получим<br>[[Image:A10-2.jpg|center|140x43px]] Учтем также, что отношения перемещений к интервалу времени равны скоростям. Поэтому<br>[[Image:A10-3.jpg|center|196x40px]] Скорости складываются геометрически, как и все другие векторы.<br> Мы получили простой и замечательный результат, который называется законом сложения скоростей: '''если тело движется относительно некоторой системы отсчета ''К<sub>1</sub>'' со скоростью [[Image:A10-5.jpg|19x29px]] и сама система отсчета''К<sub>1</sub> ''движется относительно другой системы отсчета ''К<sub>2</sub> ''со скоростью [[Image:A10-7.jpg|21x30px]], то скорость тела относительно второй системы отсчета равна геометрической сумме скоростей [[Image:A10-5.jpg|21x32px]] и [[Image:A10-6.jpg|16x27px]].''' Закон сложения скоростей справедлив и для неравномерного движения. В этом случае складываются мгновенные скорости.<br> Как и любое векторное уравнение, уравнение (1.9) представляет собой компактную запись скалярных уравнений, в данном случае - для сложения проекций скоростей движения на плоскости:<br>[[Image:A10-4.jpg|center|258x45px]] Проекции скоростей складываются алгебраически.<br> Закон сложения скоростей позволяет определять скорость тела относительно разных систем отсчета, движущихся относительно друг друга.<br> <br> | + | [[Image:A10-1.jpg|center|215x30px|A10-1.jpg]][[Image:A1.21.jpg|center|175x171px|Сложение скоростей]] Разделив левую и правую части уравнения (1.8) на [[Image:A10-8.jpg|22x16px|A10-8.jpg]], получим<br>[[Image:A10-2.jpg|center|140x43px|Сложение скоростей]] Учтем также, что отношения перемещений к интервалу времени равны [[Мгновенная_скорость|скоростям]]. Поэтому<br>[[Image:A10-3.jpg|center|196x40px|Сложение скоростей]] Скорости складываются геометрически, как и все другие векторы.<br> Мы получили простой и замечательный результат, который называется законом сложения скоростей: '''если тело движется относительно некоторой системы отсчета ''К<sub>1</sub>'' со скоростью [[Image:A10-5.jpg|19x29px|A10-5.jpg]] и сама система отсчета''К<sub>1</sub> ''движется относительно другой системы отсчета ''К<sub>2</sub> ''со скоростью [[Image:A10-7.jpg|21x30px|A10-7.jpg]], то скорость тела относительно второй системы отсчета равна геометрической сумме скоростей [[Image:A10-5.jpg|21x32px|A10-5.jpg]] и [[Image:A10-6.jpg|16x27px|A10-6.jpg]].''' Закон сложения скоростей справедлив и для неравномерного движения. В этом случае складываются мгновенные скорости.<br> Как и любое векторное уравнение, уравнение (1.9) представляет собой компактную запись скалярных уравнений, в данном случае - для сложения проекций скоростей движения на [[Плоскость._Прямая._Луч|плоскости]]:<br>[[Image:A10-4.jpg|center|258x45px|Сложение скоростей]] Проекции скоростей складываются алгебраически.<br> Закон сложения скоростей позволяет определять скорость тела относительно разных систем отсчета, движущихся относительно друг друга.<br> <br> |
| | | | |
| - | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' | + | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, [[Физика_10_класс|Физика 10 класс]]'' |
| | | | |
| | <br> <sub>Скачать календарно-тематическое планирование [[Физика и астрономия|по физике]], ответы на тесты, задания и ответы школьнику, [[Гипермаркет знаний - первый в мире!|книги и учебники]], курсы учителю [[Физика 10 класс|по физике для 10 класса]]</sub> | | <br> <sub>Скачать календарно-тематическое планирование [[Физика и астрономия|по физике]], ответы на тесты, задания и ответы школьнику, [[Гипермаркет знаний - первый в мире!|книги и учебники]], курсы учителю [[Физика 10 класс|по физике для 10 класса]]</sub> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | | | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
перемещения лодки и мяча относительно берега равны 
и 
(рис.1.20), а перемещение лодки относительно мяча равно 
. Из рисунка 1.21 видно, что 
и сама система отсчетаК1 движется относительно другой системы отсчета К2 со скоростью 
, то скорость тела относительно второй системы отсчета равна геометрической сумме скоростей 
. Закон сложения скоростей справедлив и для неравномерного движения. В этом случае складываются мгновенные скорости.
