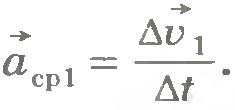|
|
|
| Строка 5: |
Строка 5: |
| | <metakeywords>Физика, 10 класс, Ускорение</metakeywords> | | <metakeywords>Физика, 10 класс, Ускорение</metakeywords> |
| | | | |
| - | При движении тел их скорости обычно меняются либо по модулю, либо по направлению, либо же одновременно как по модулю, так и по направлению.<br> Так, скорость шайбы, скользящей по льду, уменьшается с течением времени до полной ее остановки. Если взять в руки камень и разжать пальцы, то при падении камня его скорость постепенно нарастает (''рис.1.24''). <br>[[Image:A1.24.jpg|center|79x267px]]Скорость любой точки окружности точильного круга при неизменном числе оборотов в единицу времени меняется только по направлению, оставаясь постоянной по модулю (''рис.1.25''). Если бросить камень под углом к горизонту, то его скорость будет меняться и по модулю, и по направлению.<br>[[Image:A1.25.jpg|center|145x173px]] Изменение скорости тела может происходить как очень быстро (движение пули в канале ствола при выстреле из винтовки), так и сравнительно медленно (движение поезда при его отправлении). Чтобы уметь находить скорость в любой момент времени, необходимо ввести величину, характеризующую быстроту изменения скорости. Эту величину называют '''ускорением'''. Ускорение - еще одна важнейшая физическая величина.<br> Рассмотрим случай криволинейного и неравномерного движения точки. В этом случае ее скорость с течением времени изменяется как по модулю, так и по направлению. Пусть в некоторый момент времени ''t ''точка занимает положение ''М'' и имеет скорость [[Image:A11-4.jpg|15x24px]]. По прошествии промежутка времени [[Image:A11-5.jpg|24x17px]] точка займет положение''M<sub>1</sub>''и будет иметь скорость [[Image:A11-6.jpg|19x28px]] (''рис.1.26''). <br>[[Image:A1.26.jpg|center|209x177px]]Чтобы найти изменение скорости за время [[Image:A11-5.jpg|25x18px]] надо из вектора [[Image:A11-6.jpg|18x24px]] вычесть вектор [[Image:A11-4.jpg|14x23px]]: [[Image:A11-7.jpg|104x24px]].Вычитание вектора [[Image:A11-4.jpg|15x25px]] можно произвести путем прибавления к вектору [[Image:A11-6.jpg|18x27px]] вектора [[Image:A11-8.jpg|37x23px]]:<br>[[Image:A11-1.jpg|center|225x31px]] Согласно правилу сложения векторов, вектор изменения скорости [[Image:A11-9.jpg|29x27px]] направлен из начала вектора [[Image:A11-6.jpg|19x28px]] в конец вектора [[Image:A11-8.jpg|39x24px]], как это показано на ''рисунке 1.27''.<br>[[Image:A1.27.jpg|center|213x178px]] Поделив вектор [[Image:A11-9.jpg|29x26px]] на промежуток времени [[Image:A11-5.jpg|26x20px]], получим вектор, направленный так же, как и вектор изменения скорости [[Image:A11-9.jpg|29x24px]]. Этот вектор называют средним ускорением точки за промежуток времени [[Image:A11-5.jpg|29x21px]]. Обозначив его через [[Image:A11-10.jpg|34x29px]], запишем:<br>[[Image:A11-2.jpg|center|109x51px]] Найдем теперь средние ускорения точки за все меньшие и меньшие промежутки времени:<br>[[Image:A11-3.jpg|center|160x49px]] При уменьшении промежутка времени [[Image:A6-5.jpg|22x16px]] вектор [[Image:A11-9.jpg|29x24px]] уменьшается по модулю и меняется по направлению (''рис.1.28''). Соответственно средние ускорения также меняются по модулю и направлению. Но при стремлении промежутка времени [[Image:A6-5.jpg|20x16px]] к нулю отношение изменения скорости к изменению времени стремится к определенному вектору как к своему предельному значению. В механике эту величину называют ускорением точки в данный момент времени, или просто ускорением, и обозначают [[Image:A11-12.jpg|17x29px]].<br>[[Image:A1.28.jpg|center|173x145px]] '''Ускорением тела''' называется предел отношения изменения скорости [[Image:A11-11.jpg|27x21px]] к промежутку времени [[Image:A6-5.jpg|22x16px]], в течение которого это изменение произошло, при стремлении [[Image:A6-5.jpg|20x16px]] к нулю.<br> Ускорение направлено так, как в пределе, при стремлении промежутка времени [[Image:A6-5.jpg|20x16px]] к нулю, направлен вектор изменения скорости [[Image:A11-11.jpg|30x23px]]. В отличие от направления скорости, направление вектора ускорения нельзя определить, зная траекторию точки и направление движения точки по траектории. В дальнейшем на простых примерах мы увидим, как можно определить направление ускорения тела при прямолинейном и криволинейном движениях. Пока же надо запомнить, что при данном направлении скорости ускорение может иметь любое направление.<br> Могут возникнуть вопросы: ведь может существовать движение с переменным ускорением? Не следует ли ввести величину, характеризующую быстроту изменения ускорения? Конечно, такую величину ввести можно, но обычно в этом нет необходимости.<br> При движении скорость тел, как правило, изменяется. Знать быстроту ее изменения со временем, т. е. знать ускорение необходимо для вычисления скорости и определения положения тела.<br><br><br> ???<br> 1. Что такое ускорение?<br> 2. Куда направлено ускорение при прямолинейном движении тела, если модуль его скорости увеличивается? Уменьшается?<br> 3. Может ли тело иметь ускорение, если его скорость равна нулю?<br> | + | При [[Путь_при_равноускоренном_движении|движении]] тел их скорости обычно меняются либо по модулю, либо по направлению, либо же одновременно как по модулю, так и по направлению.<br> Так, скорость шайбы, скользящей по льду, уменьшается с течением времени до полной ее остановки. Если взять в руки камень и разжать пальцы, то при падении камня его скорость постепенно нарастает (''рис.1.24''). <br>[[Image:A1.24.jpg|center|79x267px|Ускорение]]Скорость любой точки окружности точильного круга при неизменном числе оборотов в единицу времени меняется только по направлению, оставаясь постоянной по модулю (''рис.1.25''). Если бросить камень под углом к горизонту, то его скорость будет меняться и по модулю, и по направлению.<br>[[Image:A1.25.jpg|center|145x173px|Ускорение]] Изменение скорости тела может происходить как очень быстро (движение пули в канале ствола при выстреле из винтовки), так и сравнительно медленно (движение поезда при его отправлении). Чтобы уметь находить скорость в любой момент времени, необходимо ввести величину, характеризующую быстроту изменения скорости. Эту величину называют '''ускорением'''. [[Единица_ускорения|Ускорение]] - еще одна важнейшая физическая величина.<br> Рассмотрим случай криволинейного и неравномерного движения точки. В этом случае ее скорость с течением времени изменяется как по модулю, так и по направлению. Пусть в некоторый момент времени ''t ''точка занимает положение ''М'' и имеет скорость [[Image:A11-4.jpg|15x24px|A11-4.jpg]]. По прошествии промежутка времени [[Image:A11-5.jpg|24x17px|A11-5.jpg]] точка займет положение''M<sub>1</sub>''и будет иметь скорость [[Image:A11-6.jpg|19x28px|A11-6.jpg]] (''рис.1.26''). <br>[[Image:A1.26.jpg|center|209x177px|Ускорение]]Чтобы найти изменение скорости за время [[Image:A11-5.jpg|25x18px|A11-5.jpg]] надо из вектора [[Image:A11-6.jpg|18x24px|A11-6.jpg]] вычесть вектор [[Image:A11-4.jpg|14x23px|A11-4.jpg]]: [[Image:A11-7.jpg|104x24px|Ускорение]].Вычитание вектора [[Image:A11-4.jpg|15x25px|A11-4.jpg]] можно произвести путем прибавления к вектору [[Image:A11-6.jpg|18x27px|A11-6.jpg]] [[Вектор_магнитной_индукции._Линии_магнитной_индукции|вектора]] [[Image:A11-8.jpg|37x23px|A11-8.jpg]]:<br>[[Image:A11-1.jpg|center|225x31px|Ускорение]] Согласно правилу сложения векторов, вектор изменения скорости [[Image:A11-9.jpg|29x27px|A11-9.jpg]] направлен из начала вектора [[Image:A11-6.jpg|19x28px|A11-6.jpg]] в конец вектора [[Image:A11-8.jpg|39x24px|A11-8.jpg]], как это показано на ''рисунке 1.27''.<br>[[Image:A1.27.jpg|center|213x178px|Ускорение]] Поделив вектор [[Image:A11-9.jpg|29x26px|A11-9.jpg]] на промежуток времени [[Image:A11-5.jpg|26x20px|A11-5.jpg]], получим вектор, направленный так же, как и вектор изменения скорости [[Image:A11-9.jpg|29x24px|A11-9.jpg]]. Этот вектор называют средним ускорением точки за промежуток времени [[Image:A11-5.jpg|29x21px|A11-5.jpg]]. Обозначив его через [[Image:A11-10.jpg|34x29px|A11-10.jpg]], запишем:<br>[[Image:A11-2.jpg|center|109x51px|Ускорение]] Найдем теперь средние ускорения точки за все меньшие и меньшие промежутки времени:<br>[[Image:A11-3.jpg|center|160x49px|Ускорение]] При уменьшении промежутка времени [[Image:A6-5.jpg|22x16px|A6-5.jpg]] вектор [[Image:A11-9.jpg|29x24px|A11-9.jpg]] уменьшается по модулю и меняется по направлению (''рис.1.28''). Соответственно средние ускорения также меняются по модулю и направлению. Но при стремлении промежутка времени [[Image:A6-5.jpg|20x16px|A6-5.jpg]] к нулю отношение изменения скорости к изменению времени стремится к определенному вектору как к своему предельному значению. В механике эту величину называют ускорением точки в данный момент времени, или просто ускорением, и обозначают [[Image:A11-12.jpg|17x29px|A11-12.jpg]].<br>[[Image:A1.28.jpg|center|173x145px|Ускорение]] '''[[Скорость_при_движении_с_постоянным_ускорением|Ускорением тела]]''' называется предел отношения изменения скорости [[Image:A11-11.jpg|27x21px|A11-11.jpg]] к промежутку времени [[Image:A6-5.jpg|22x16px|A6-5.jpg]], в течение которого это изменение произошло, при стремлении [[Image:A6-5.jpg|20x16px|A6-5.jpg]] к нулю.<br> Ускорение направлено так, как в пределе, при стремлении промежутка времени [[Image:A6-5.jpg|20x16px|A6-5.jpg]] к нулю, направлен вектор изменения скорости [[Image:A11-11.jpg|30x23px|A11-11.jpg]]. В отличие от направления скорости, направление вектора ускорения нельзя определить, зная траекторию точки и направление движения точки по траектории. В дальнейшем на простых примерах мы увидим, как можно определить направление ускорения тела при прямолинейном и криволинейном движениях. Пока же надо запомнить, что при данном направлении скорости ускорение может иметь любое направление.<br> Могут возникнуть вопросы: ведь может существовать движение с переменным ускорением? Не следует ли ввести величину, характеризующую быстроту изменения ускорения? Конечно, такую величину ввести можно, но обычно в этом нет необходимости.<br> При движении скорость тел, как правило, изменяется. Знать быстроту ее изменения со временем, т. е. знать ускорение необходимо для вычисления скорости и определения положения тела.<br><br><br> ???<br> 1. Что такое ускорение?<br> 2. Куда направлено ускорение при прямолинейном движении тела, если модуль его скорости увеличивается? Уменьшается?<br> 3. Может ли тело иметь ускорение, если его скорость равна нулю?<br> |
| | | | |
| - | <br> ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' | + | <br> ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, [[Физика_10_класс|Физика 10 класс]]'' |
| | | | |
| | <br> <sub>Планирования [[Физика и астрономия|по физике]], учебники и книги онлайн, курсы и задания [[Физика 10 класс|по физике для 10 класса]]</sub> | | <br> <sub>Планирования [[Физика и астрономия|по физике]], учебники и книги онлайн, курсы и задания [[Физика 10 класс|по физике для 10 класса]]</sub> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | | | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 12:55, 4 июля 2012
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Ускорение
При движении тел их скорости обычно меняются либо по модулю, либо по направлению, либо же одновременно как по модулю, так и по направлению.
Так, скорость шайбы, скользящей по льду, уменьшается с течением времени до полной ее остановки. Если взять в руки камень и разжать пальцы, то при падении камня его скорость постепенно нарастает (рис.1.24).
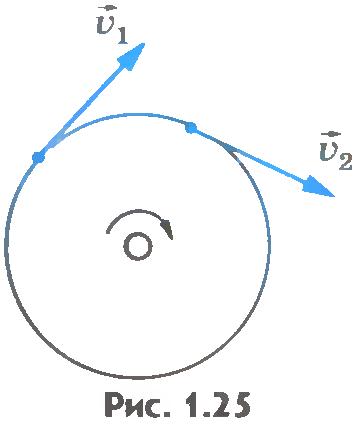
Скорость любой точки окружности точильного круга при неизменном числе оборотов в единицу времени меняется только по направлению, оставаясь постоянной по модулю (рис.1.25). Если бросить камень под углом к горизонту, то его скорость будет меняться и по модулю, и по направлению.
Изменение скорости тела может происходить как очень быстро (движение пули в канале ствола при выстреле из винтовки), так и сравнительно медленно (движение поезда при его отправлении). Чтобы уметь находить скорость в любой момент времени, необходимо ввести величину, характеризующую быстроту изменения скорости. Эту величину называют ускорением. Ускорение - еще одна важнейшая физическая величина.
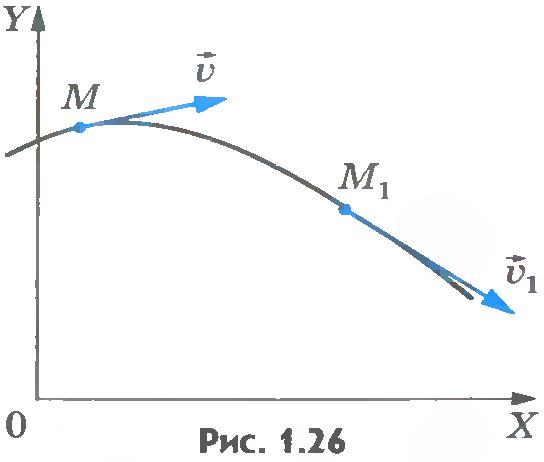
Рассмотрим случай криволинейного и неравномерного движения точки. В этом случае ее скорость с течением времени изменяется как по модулю, так и по направлению. Пусть в некоторый момент времени t точка занимает положение М и имеет скорость 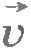 . По прошествии промежутка времени . По прошествии промежутка времени  точка займет положениеM1и будет иметь скорость точка займет положениеM1и будет иметь скорость 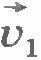 (рис.1.26). (рис.1.26).
Чтобы найти изменение скорости за время  надо из вектора надо из вектора 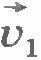 вычесть вектор вычесть вектор 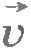 : : 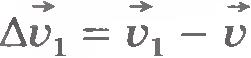 .Вычитание вектора .Вычитание вектора 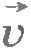 можно произвести путем прибавления к вектору можно произвести путем прибавления к вектору 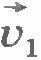 вектора вектора 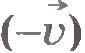 : :
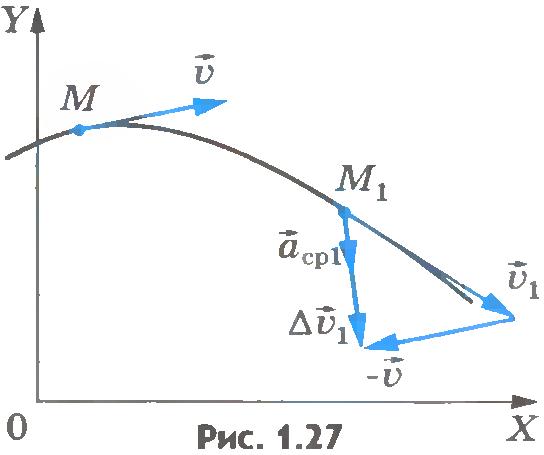
Согласно правилу сложения векторов, вектор изменения скорости 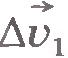 направлен из начала вектора направлен из начала вектора 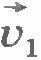 в конец вектора в конец вектора 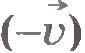 , как это показано на рисунке 1.27. , как это показано на рисунке 1.27.
Поделив вектор 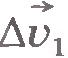 на промежуток времени на промежуток времени  , получим вектор, направленный так же, как и вектор изменения скорости , получим вектор, направленный так же, как и вектор изменения скорости 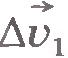 . Этот вектор называют средним ускорением точки за промежуток времени . Этот вектор называют средним ускорением точки за промежуток времени  . Обозначив его через . Обозначив его через 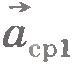 , запишем: , запишем:
Найдем теперь средние ускорения точки за все меньшие и меньшие промежутки времени:
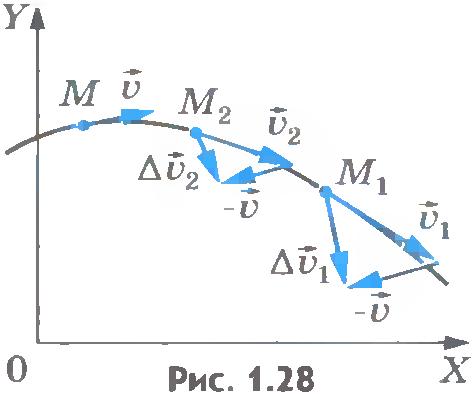
При уменьшении промежутка времени  вектор вектор 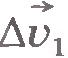 уменьшается по модулю и меняется по направлению (рис.1.28). Соответственно средние ускорения также меняются по модулю и направлению. Но при стремлении промежутка времени уменьшается по модулю и меняется по направлению (рис.1.28). Соответственно средние ускорения также меняются по модулю и направлению. Но при стремлении промежутка времени  к нулю отношение изменения скорости к изменению времени стремится к определенному вектору как к своему предельному значению. В механике эту величину называют ускорением точки в данный момент времени, или просто ускорением, и обозначают к нулю отношение изменения скорости к изменению времени стремится к определенному вектору как к своему предельному значению. В механике эту величину называют ускорением точки в данный момент времени, или просто ускорением, и обозначают 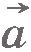 . .
Ускорением тела называется предел отношения изменения скорости 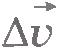 к промежутку времени к промежутку времени  , в течение которого это изменение произошло, при стремлении , в течение которого это изменение произошло, при стремлении  к нулю. к нулю.
Ускорение направлено так, как в пределе, при стремлении промежутка времени  к нулю, направлен вектор изменения скорости к нулю, направлен вектор изменения скорости 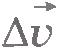 . В отличие от направления скорости, направление вектора ускорения нельзя определить, зная траекторию точки и направление движения точки по траектории. В дальнейшем на простых примерах мы увидим, как можно определить направление ускорения тела при прямолинейном и криволинейном движениях. Пока же надо запомнить, что при данном направлении скорости ускорение может иметь любое направление. . В отличие от направления скорости, направление вектора ускорения нельзя определить, зная траекторию точки и направление движения точки по траектории. В дальнейшем на простых примерах мы увидим, как можно определить направление ускорения тела при прямолинейном и криволинейном движениях. Пока же надо запомнить, что при данном направлении скорости ускорение может иметь любое направление.
Могут возникнуть вопросы: ведь может существовать движение с переменным ускорением? Не следует ли ввести величину, характеризующую быстроту изменения ускорения? Конечно, такую величину ввести можно, но обычно в этом нет необходимости.
При движении скорость тел, как правило, изменяется. Знать быстроту ее изменения со временем, т. е. знать ускорение необходимо для вычисления скорости и определения положения тела.
???
1. Что такое ускорение?
2. Куда направлено ускорение при прямолинейном движении тела, если модуль его скорости увеличивается? Уменьшается?
3. Может ли тело иметь ускорение, если его скорость равна нулю?
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Планирования по физике, учебники и книги онлайн, курсы и задания по физике для 10 класса
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|