|
|
|
| Строка 5: |
Строка 5: |
| | <metakeywords>Физика, 10 класс, Способы описания, движения, Система отсчета</metakeywords> | | <metakeywords>Физика, 10 класс, Способы описания, движения, Система отсчета</metakeywords> |
| | | | |
| - | Если тело можно считать точкой, то для описания его движения нужно научиться рассчитывать положение точки в любой момент времени относительно выбранного тела отсчета.<br> Существует несколько способов описания, или, что одно и то же, задания, движения точки. Рассмотрим два из них, которые наиболее часто применяются.<br> '''Координатный способ.''' Будем задавать положение точки с помощью координат (''рис.1.7''). Если точка движется, то ее координаты изменяются с течением времени. Так как координаты точки зависят от времени, то можно сказать, что они являются функциями времени. | + | Если тело можно считать точкой, то для описания его движения нужно научиться рассчитывать положение точки в любой момент времени относительно выбранного тела отсчета.<br> Существует несколько способов описания, или, что одно и то же, задания, движения точки. Рассмотрим два из них, которые наиболее часто применяются.<br> '''Координатный способ.''' Будем задавать положение точки с помощью координат (''рис.1.7''). Если точка движется, то ее координаты изменяются с течением времени. Так как координаты точки зависят от времени, то можно сказать, что они являются функциями [[Урок_18._Меры_времени._Календарь|времени]]. |
| | | | |
| - | [[Image:A1.7.jpg|center|220x173px]]Математически это принято записывать в виде<br>[[Image:A5-1.jpg|center|219x88px]] Уравнения (1.1) называют '''кинематическими уравнениями движения точки''', записанными в координатной форме. Если они известны, то для каждого момента времени мы сможем рассчитать координаты точки, а следовательно, и ее положение относительно выбранного тела отсчета. Вид уравнений (1.1) для каждого конкретного движения будет вполне определенным.<br> Линия, по которой движется точка в пространстве, называется '''траекторией'''.<br> В зависимости от формы траектории все движения точки делятся на прямолинейные и криволинейные. Если траекторией является прямая линия, движение точки называется ''прямолинейным'', а если кривая - ''криволинейным''.<br> '''Векторный способ'''. Положение точки можно задать, как известно, и с помощью радиус-вектора. При движении материальной точки радиус-вектор, определяющий ее положение, с течением времени изменяется (поворачивается и меняет длину; ''рис.1.8''), т. е. является функцией времени:<br>[[Image:A5-2.jpg|center|200x31px]][[Image:A1.8.jpg|center|192x177px]] Последнее уравнение есть закон движения точки, записанный в векторной форме. Если он известен, то мы можем для любого момента времени рассчитать радиус-вектор точки, а значит, определить ее положение. Таким образом, задание трех скалярных уравнений (1.1) равносильно заданию одного векторного уравнения (1.2).<br> '''Система отсчета'''. Движение любого тела есть движение относительное. Это значит, что движение данного тела может быть совершенно различным по отношению к другим телам.<br> Так, если для наблюдателя, находящегося на палубе плывущего теплохода, какой-нибудь лежащий на ней предмет неподвижен, для наблюдателя, находящегося на берегу, он движется.<br> В безветренную погоду капли дождя падают относительно земли по вертикальным линиям. Но относительно вагона, движущегося равномерно и прямолинейно, эти же капли движутся по прямым, наклонным к вертикали. Если какое-либо тело находится в покое по отношению к Земле, то оно движется по отношению к Солнцу. Таким образом, изучая движение интересующего нас тела, мы обязательно должны указать, относительно какого тела это движение рассматривается.<br> Тело, относительно которого рассматривается движение, называется '''телом отсчета'''.<br> Чтобы рассчитать положение точки (тела) относительно выбранного тела отсчета в зависимости от времени, надо не только связать с ним систему координат, но и суметь измерить время. Время измеряют с помощью часов. Современные часы - это сложные устройства. Они позволяют измерять время в секундах с точностью до тринадцатого знака после запятой. Естественно, ни одни механические часы такой точности обеспечить не могут. Так, самые точные в мире механические часы, циферблат которых мы можем каждый день видеть на телеэкране, в десять тысяч раз менее точны, чем Государственный эталон времени. Если эталонные часы не корректировать, то на одну секунду они убегут или отстанут за триста тысяч лет. Понятно, что в быту нет необходимости измерять время с очень большой точностью. Но для физических исследований, космонавтики, геодезии, радиоастрономии, управления воздушным транспортом высокая точность в измерении времени просто необходима. От точности измерения времени зависит точность, с которой мы сумеем рассчитать положение тела в какой-либо момент времени.<br> Совокупность тела отсчета, связанной с ним системы координат и часов называют '''системой отсчета'''. На рисунке 1.9 показана система отсчета, выбранная для рассмотрения полета брошенного мяча. В данном случае телом отсчета является дом, оси координат выбраны так, что мяч летит в плоскости ''ХОY'', для определения времени берется секундомер.<br>Кинематические уравнения движения, записанные в координатной или векторной форме, позволяют определить положение точки в любой момент времени.<br> | + | [[Image:A1.7.jpg|center|220x173px|Система отсчета]]Математически это принято записывать в виде<br>[[Image:A5-1.jpg|center|219x88px|Система отсчета]] Уравнения (1.1) называют '''кинематическими уравнениями движения точки''', записанными в координатной форме. Если они известны, то для каждого момента времени мы сможем рассчитать координаты точки, а следовательно, и ее положение относительно выбранного тела отсчета. Вид уравнений (1.1) для каждого конкретного движения будет вполне определенным.<br> Линия, по которой движется точка в пространстве, называется '''[[Траекторія_руху._Шлях_і_переміщення.|траекторией]]'''.<br> В зависимости от формы траектории все движения точки делятся на прямолинейные и криволинейные. Если траекторией является прямая линия, движение точки называется ''прямолинейным'', а если кривая - ''криволинейным''.<br> '''Векторный способ'''. Положение точки можно задать, как известно, и с помощью радиус-вектора. При движении материальной точки радиус-вектор, определяющий ее положение, с течением времени изменяется (поворачивается и меняет длину; ''рис.1.8''), т. е. является функцией времени:<br>[[Image:A5-2.jpg|center|200x31px|Система отсчета]][[Image:A1.8.jpg|center|192x177px|Система отсчета]] Последнее уравнение есть закон движения точки, записанный в [[Векторная_графика._Полные_уроки|векторной]] форме. Если он известен, то мы можем для любого момента времени рассчитать радиус-вектор точки, а значит, определить ее положение. Таким образом, задание трех скалярных уравнений (1.1) равносильно заданию одного векторного уравнения (1.2).<br> '''Система отсчета'''. Движение любого тела есть движение относительное. Это значит, что движение данного тела может быть совершенно различным по отношению к другим телам.<br> Так, если для наблюдателя, находящегося на палубе плывущего теплохода, какой-нибудь лежащий на ней предмет неподвижен, для наблюдателя, находящегося на берегу, он движется.<br> В безветренную погоду капли дождя падают относительно земли по вертикальным линиям. Но относительно вагона, движущегося равномерно и прямолинейно, эти же капли движутся по прямым, наклонным к вертикали. Если какое-либо тело находится в покое по отношению к Земле, то оно движется по отношению к Солнцу. Таким образом, изучая движение интересующего нас тела, мы обязательно должны указать, относительно какого тела это движение рассматривается.<br> Тело, относительно которого рассматривается движение, называется '''телом отсчета'''.<br> Чтобы рассчитать положение точки (тела) относительно выбранного тела отсчета в зависимости от времени, надо не только связать с ним систему координат, но и суметь измерить время. Время измеряют с помощью часов. Современные часы - это сложные устройства. Они позволяют измерять время в секундах с точностью до тринадцатого знака после запятой. Естественно, ни одни механические часы такой точности обеспечить не могут. Так, самые точные в мире механические часы, циферблат которых мы можем каждый день видеть на телеэкране, в десять тысяч раз менее точны, чем Государственный эталон времени. Если эталонные часы не корректировать, то на одну секунду они убегут или отстанут за триста тысяч лет. Понятно, что в быту нет необходимости измерять время с очень большой точностью. Но для [[Физические_свойства_металлов|физических]] исследований, космонавтики, геодезии, радиоастрономии, управления воздушным транспортом высокая точность в измерении времени просто необходима. От точности измерения времени зависит точность, с которой мы сумеем рассчитать положение тела в какой-либо момент времени.<br> Совокупность тела отсчета, связанной с ним системы координат и часов называют '''системой отсчета'''. На рисунке 1.9 показана система отсчета, выбранная для рассмотрения полета брошенного мяча. В данном случае телом отсчета является дом, оси [[Метод_координат|координат]] выбраны так, что мяч летит в плоскости ''ХОY'', для определения времени берется секундомер.<br>Кинематические уравнения движения, записанные в координатной или векторной форме, позволяют определить положение точки в любой момент времени.<br> |
| | | | |
| - | [[Image:A1.9.jpg|center|224x189px]]<br> ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' | + | [[Image:A1.9.jpg|center|224x189px|Система отсчета]]<br> ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' |
| | | | |
| | <br> <sub>Материалы [[Физика и астрономия|по физике]], задание и ответы по классам, планы конспектов уроков [[Физика 10 класс|по физике для 10 класса]]</sub> | | <br> <sub>Материалы [[Физика и астрономия|по физике]], задание и ответы по классам, планы конспектов уроков [[Физика 10 класс|по физике для 10 класса]]</sub> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | | | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 12:26, 4 июля 2012
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Способы описания движения. Система отсчета
Если тело можно считать точкой, то для описания его движения нужно научиться рассчитывать положение точки в любой момент времени относительно выбранного тела отсчета.
Существует несколько способов описания, или, что одно и то же, задания, движения точки. Рассмотрим два из них, которые наиболее часто применяются.
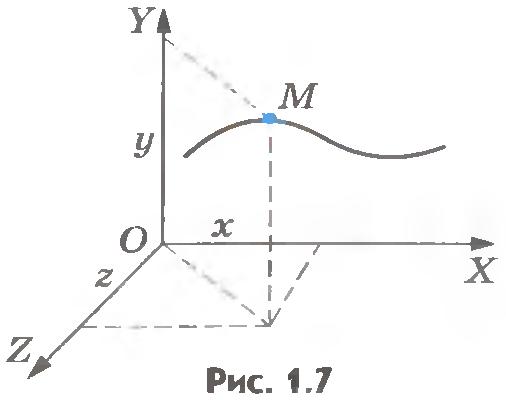
Координатный способ. Будем задавать положение точки с помощью координат (рис.1.7). Если точка движется, то ее координаты изменяются с течением времени. Так как координаты точки зависят от времени, то можно сказать, что они являются функциями времени.
Математически это принято записывать в виде
Уравнения (1.1) называют кинематическими уравнениями движения точки, записанными в координатной форме. Если они известны, то для каждого момента времени мы сможем рассчитать координаты точки, а следовательно, и ее положение относительно выбранного тела отсчета. Вид уравнений (1.1) для каждого конкретного движения будет вполне определенным.
Линия, по которой движется точка в пространстве, называется траекторией.
В зависимости от формы траектории все движения точки делятся на прямолинейные и криволинейные. Если траекторией является прямая линия, движение точки называется прямолинейным, а если кривая - криволинейным.
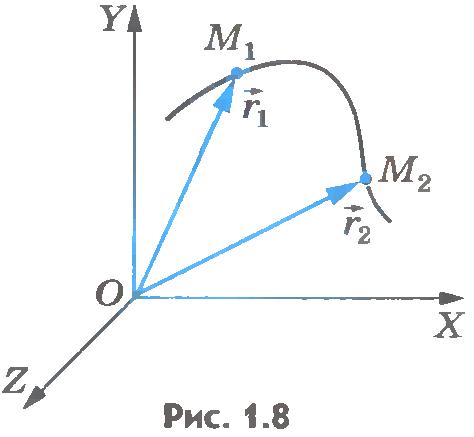
Векторный способ. Положение точки можно задать, как известно, и с помощью радиус-вектора. При движении материальной точки радиус-вектор, определяющий ее положение, с течением времени изменяется (поворачивается и меняет длину; рис.1.8), т. е. является функцией времени:
Последнее уравнение есть закон движения точки, записанный в векторной форме. Если он известен, то мы можем для любого момента времени рассчитать радиус-вектор точки, а значит, определить ее положение. Таким образом, задание трех скалярных уравнений (1.1) равносильно заданию одного векторного уравнения (1.2).
Система отсчета. Движение любого тела есть движение относительное. Это значит, что движение данного тела может быть совершенно различным по отношению к другим телам.
Так, если для наблюдателя, находящегося на палубе плывущего теплохода, какой-нибудь лежащий на ней предмет неподвижен, для наблюдателя, находящегося на берегу, он движется.
В безветренную погоду капли дождя падают относительно земли по вертикальным линиям. Но относительно вагона, движущегося равномерно и прямолинейно, эти же капли движутся по прямым, наклонным к вертикали. Если какое-либо тело находится в покое по отношению к Земле, то оно движется по отношению к Солнцу. Таким образом, изучая движение интересующего нас тела, мы обязательно должны указать, относительно какого тела это движение рассматривается.
Тело, относительно которого рассматривается движение, называется телом отсчета.
Чтобы рассчитать положение точки (тела) относительно выбранного тела отсчета в зависимости от времени, надо не только связать с ним систему координат, но и суметь измерить время. Время измеряют с помощью часов. Современные часы - это сложные устройства. Они позволяют измерять время в секундах с точностью до тринадцатого знака после запятой. Естественно, ни одни механические часы такой точности обеспечить не могут. Так, самые точные в мире механические часы, циферблат которых мы можем каждый день видеть на телеэкране, в десять тысяч раз менее точны, чем Государственный эталон времени. Если эталонные часы не корректировать, то на одну секунду они убегут или отстанут за триста тысяч лет. Понятно, что в быту нет необходимости измерять время с очень большой точностью. Но для физических исследований, космонавтики, геодезии, радиоастрономии, управления воздушным транспортом высокая точность в измерении времени просто необходима. От точности измерения времени зависит точность, с которой мы сумеем рассчитать положение тела в какой-либо момент времени.
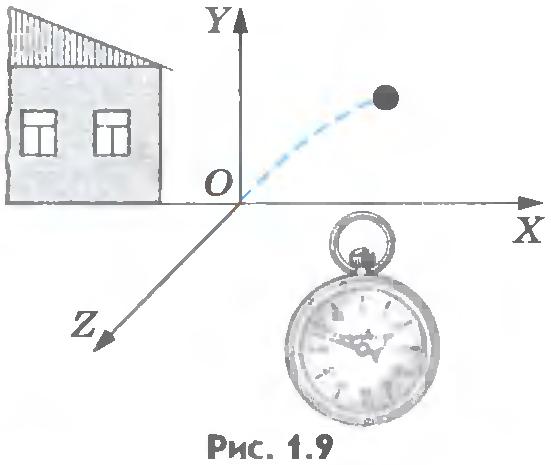
Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета. На рисунке 1.9 показана система отсчета, выбранная для рассмотрения полета брошенного мяча. В данном случае телом отсчета является дом, оси координат выбраны так, что мяч летит в плоскости ХОY, для определения времени берется секундомер.
Кинематические уравнения движения, записанные в координатной или векторной форме, позволяют определить положение точки в любой момент времени.
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Материалы по физике, задание и ответы по классам, планы конспектов уроков по физике для 10 класса
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|