|
|
|
| Строка 5: |
Строка 5: |
| | <metakeywords>Физика, 10 класс, Инерциальные системы, отсчета и принцип, относительности в механике</metakeywords> | | <metakeywords>Физика, 10 класс, Инерциальные системы, отсчета и принцип, относительности в механике</metakeywords> |
| | | | |
| - | Законы механики справедливы в инерциальных системах отсчета. Какие системы отсчета можно считать инерциальными?<br> '''Инерциальные и неинерциальные системы отсчета.''' Легко понять, что любая система отсчета, которая движется равномерно и прямолинейно относительно данной инерциальной системы отсчета, также является инерциальной. В самом деле, если тело относительно определенной инерциальной системы отсчета движется с постоянной скоростью [[Image:A28-2.jpg|18x28px]], то по отношению к системе отсчета, которая сама движется со скоростью [[Image:A28-3.jpg|13x21px]], это тело согласно закону сложения скоростей будет двигаться с некоторой новой, но также постоянной скоростью [[Image:A28-4.jpg|19x26px]].<br> Ускорение тела в обеих системах отсчета равно нулю.<br> Напротив, любая система отсчета, движущаяся с ускорением относительно инерциальной системы отсчета, уже будет неинерциальной. Действительно, если [[Image:A28-5.jpg|89x26px]], а скорость [[Image:A28-3.jpg|15x24px]] изменяется, то скорость [[Image:A28-4.jpg|19x24px]] также будет меняться с течением времени: [[Image:A28-6.jpg|86x24px]].<br> Следовательно, характер движения тела будет изменяться при переходе от одной системы отсчета к другой.<br> Так как систему отсчета, связанную с Землей, можно приближенно рассматривать как инерциальную, то и системы отсчета, связанные с поездом, движущимся с постоянной скоростью, или с кораблем, плывущим по прямой с неизменной скоростью, также будут инерциальными. Но как только поезд начнет увеличивать свою скорость, связанная с ним система отсчета перестанет быть инерциальной. Закон инерции и второй закон Ньютона перестанут выполняться, если рассматривать движение по отношению к таким системам.<br> '''Геоцентрическая система отсчета инерциальна лишь приближенно.''' В действительности геоцентрическая система не является строго инерциальной. Наиболее близка к инерциальной система отсчета, связанная с Солнцем и неподвижными звездами. Земля же движется по отношению к этой системе отсчета с ускорением. Во-первых, она вращается вокруг своей оси и, во-вторых, движется по замкнутой орбите вокруг Солнца.<br> Ускорение, обусловленное обращением Земли вокруг Солнца, очень мало, так как велик период обращения (год). Значительно больше (примерно в 6 раз) ускорение, возникающее из-за вращения Земли вокруг оси с периодом ''Т'' = 24 ч. Но и оно невелико. На поверхности Земли у экватора, где это ускорение наибольшее, оно равно:<br>[[Image:A28-1.jpg|center|271x45px]]т. е. составляет всего 0,35% от ускорения свободного падения ''g''=9,8 м/с<sup>2</sup>. Именно поэтому систему отсчета, связанную с Землей, можно приближенно рассматривать как инерциальную.<br> '''Доказательство вращения Земли.''' Однако существуют явления, которые нельзя объяснить, если считать геоцентрическую систему отсчета инерциальной. К ним относится вращение относительно Земли плоскости колебаний маятника в знаменитом опыте Фуко, доказывающем вращение Земли.<br> Рассмотрим колебания маятника в гелиоцентрической инерциальной системе отсчета. Для большей наглядности и простоты будем считать, что опыт проводится на полюсе.<br> Пусть в начальный момент маятник отклоняют от положения равновесия. Действующие на маятник сила притяжения к Земле [[Image:A28-7.jpg|19x26px]] и сила упругости подвеса маятника [[Image:A28-8.jpg|15x22px]] лежат в той же вертикальной плоскости (''рис.3.14''). Согласно второму закону Ньютона ускорение маятника совпадает по направлению с равнодействующей силой [[Image:F28-9.jpg|15x22px]] и поэтому лежит в той же вертикальной плоскости. А это значит, что с течением времени плоскость колебаний маятника в инерциальной системе отсчета должна оставаться неизменной. Так и происходит в гелиоцентрической системе. Однако система отсчета, связанная с Землей, не является инерциальной, и относительно нее плоскость колебаний маятника поворачивается вследствие вращения Земли. Чтобы это обнаружить, необходимо подвес сделать таким, чтобы трение в нем было мало, а сам маятник - достаточно массивным. Иначе трение в подвесе заставит плоскость колебаний следовать за вращением Земли. <br>[[Image:A3.14.jpg|center|194x258px]] Смещение плоскости колебаний маятника относительно Земли становится заметным уже через несколько минут. На средних широтах колебания маятника будут выглядеть несколько сложнее, но суть явления не изменится. Впервые такой опыт был произведен Ж. Фуко в 1850 г. в Париже.<br> '''Равномерное прямолинейное движение не влияет на механические процессы.''' Галилей первым обратил внимание на то, что равномерное прямолинейное движение по отношению к Земле совершенно не сказывается на течении всех механических явлений.<br> Допустим, вы находитесь в каюте корабля или в вагоне поезда, движущегося плавно, без толчков. Вы можете спокойно играть в бадминтон или пинг-понг, как и на земле. Мяч или волан будет по отношению к стенам и полу перемещаться точно так же, как и по отношению к Земле при игре в обычных условиях. Если не посмотреть в окно, то с уверенностью нельзя сказать, что же происходит с поездом: движется он или стоит.<br> Если в движущемся с постоянной скоростью вагоне изучать падение тел, колебания маятника и другие явления, то результаты будут точно такими же, как и при исследовании этих явлений на Земле. Когда современный реактивный самолет летит со скоростью около 1000 км/ч, в его салоне не происходит ничего, что позволяло бы ощутить эту огромную скорость. Вы можете есть, спать, играть в шахматы, чувствуя себя как дома.<br> Лишь при резком торможении поезда нужно прилагать дополнительные усилия, чтобы устоять на ногах. При большой болтанке самолета или качке парохода на большой волне об игре с мячом не может быть и речи. Все предметы приходится закреплять, чтобы они оставались на своих местах.<br> '''Принцип относительности.''' На основании подобных наблюдений можно сформулировать один из самых фундаментальных законов природы - '''''принцип относительности:'''''<br> '''''Все механические процессы протекают одинаково во всех инерциальных системах отсчета.'''''<br> Это утверждение известно как принцип относительности в механике. Его еще называют принципом относительности Галилея.<br> Не нужно думать, что выполнение принципа относительности означает полную тождественность движения одного и того же тела относительно различных инерциальных систем отсчета. Тождественны лишь законы динамики. Законы движения тел определяются не только законами динамики, но и начальными скоростями и начальными координатами тел. А начальные скорости и начальные координаты данного тела относительно разных систем отсчета различны.<br> Так, камень будет падать отвесно, если его начальная скорость равна нулю по отношению к Земле. В равномерно движущемся поезде камень также будет падать отвесно по отношению к стенам вагона, если начальная скорость камня по отношению к поезду равна нулю. Но, с точки зрения наблюдателя на Земле, камень, падающий отвесно в поезде, будет двигаться по параболе (''рис.3.15, 3.16''). Дело в том, что начальная скорость камня по отношению к системе отсчета, связанной с Землей, отлична от нуля и равна скорости поезда.<br>
| + | Законы [[Основное_утверждение_механики|механики]] справедливы в инерциальных системах отсчета. Какие системы отсчета можно считать инерциальными?<br> '''Инерциальные и неинерциальные системы отсчета.''' Легко понять, что любая система отсчета, которая движется равномерно и прямолинейно относительно данной инерциальной системы отсчета, также является инерциальной. В самом деле, если тело относительно определенной инерциальной системы отсчета движется с постоянной скоростью [[Image:A28-2.jpg|18x28px|A28-2.jpg]], то по отношению к системе отсчета, которая сама движется со скоростью [[Image:A28-3.jpg|13x21px|A28-3.jpg]], это тело согласно закону сложения скоростей будет двигаться с некоторой новой, но также постоянной скоростью [[Image:A28-4.jpg|19x26px|A28-4.jpg]].<br> Ускорение тела в обеих системах отсчета равно нулю.<br> Напротив, любая система отсчета, движущаяся с [[Единица_ускорения|ускорением]] относительно инерциальной системы отсчета, уже будет неинерциальной. Действительно, если [[Image:A28-5.jpg|89x26px|A28-5.jpg]], а скорость [[Image:A28-3.jpg|15x24px|A28-3.jpg]] изменяется, то скорость [[Image:A28-4.jpg|19x24px|A28-4.jpg]] также будет меняться с течением времени: [[Image:A28-6.jpg|86x24px|A28-6.jpg]].<br> Следовательно, характер движения тела будет изменяться при переходе от одной системы отсчета к другой.<br> Так как систему отсчета, связанную с Землей, можно приближенно рассматривать как инерциальную, то и системы отсчета, связанные с поездом, движущимся с постоянной скоростью, или с кораблем, плывущим по прямой с неизменной скоростью, также будут инерциальными. Но как только поезд начнет увеличивать свою скорость, связанная с ним система отсчета перестанет быть инерциальной. Закон инерции и второй закон Ньютона перестанут выполняться, если рассматривать движение по отношению к таким системам.<br> '''Геоцентрическая система отсчета инерциальна лишь приближенно.''' В действительности геоцентрическая система не является строго инерциальной. Наиболее близка к инерциальной система отсчета, связанная с Солнцем и неподвижными звездами. Земля же движется по отношению к этой системе отсчета с ускорением. Во-первых, она вращается вокруг своей оси и, во-вторых, движется по замкнутой орбите вокруг [[Солнце|Солнца]].<br> Ускорение, обусловленное обращением Земли вокруг Солнца, очень мало, так как велик период обращения (год). Значительно больше (примерно в 6 раз) ускорение, возникающее из-за вращения Земли вокруг оси с периодом ''Т'' = 24 ч. Но и оно невелико. На поверхности Земли у экватора, где это ускорение наибольшее, оно равно:<br>[[Image:A28-1.jpg|center|271x45px|A28-1.jpg]]т. е. составляет всего 0,35% от ускорения свободного падения ''g''=9,8 м/с<sup>2</sup>. Именно поэтому систему отсчета, связанную с Землей, можно приближенно рассматривать как инерциальную.<br> '''Доказательство вращения Земли.''' Однако существуют явления, которые нельзя объяснить, если считать геоцентрическую систему отсчета инерциальной. К ним относится вращение относительно Земли плоскости колебаний маятника в знаменитом опыте Фуко, доказывающем вращение Земли.<br> Рассмотрим колебания маятника в гелиоцентрической инерциальной системе отсчета. Для большей наглядности и простоты будем считать, что опыт проводится на полюсе.<br> Пусть в начальный момент маятник отклоняют от положения равновесия. Действующие на маятник сила притяжения к Земле [[Image:A28-7.jpg|19x26px|A28-7.jpg]] и сила упругости подвеса [[Математический_маятник|маятника]] [[Image:A28-8.jpg|15x22px|A28-8.jpg]] лежат в той же вертикальной плоскости (''рис.3.14''). Согласно второму закону Ньютона ускорение маятника совпадает по направлению с равнодействующей силой [[Image:F28-9.jpg|15x22px|F28-9.jpg]] и поэтому лежит в той же вертикальной плоскости. А это значит, что с течением времени плоскость колебаний маятника в инерциальной системе отсчета должна оставаться неизменной. Так и происходит в гелиоцентрической системе. Однако система отсчета, связанная с Землей, не является инерциальной, и относительно нее плоскость колебаний маятника поворачивается вследствие вращения Земли. Чтобы это обнаружить, необходимо подвес сделать таким, чтобы трение в нем было мало, а сам маятник - достаточно массивным. Иначе трение в подвесе заставит плоскость колебаний следовать за вращением Земли. <br>[[Image:A3.14.jpg|center|194x258px|Инерциальные системы отсчета]] Смещение плоскости колебаний маятника относительно Земли становится заметным уже через несколько минут. На средних широтах колебания маятника будут выглядеть несколько сложнее, но суть явления не изменится. Впервые такой опыт был произведен Ж. Фуко в 1850 г. в Париже.<br> '''Равномерное прямолинейное движение не влияет на механические процессы.''' Галилей первым обратил внимание на то, что равномерное прямолинейное движение по отношению к Земле совершенно не сказывается на течении всех механических явлений.<br> Допустим, вы находитесь в каюте корабля или в вагоне поезда, движущегося плавно, без толчков. Вы можете спокойно играть в бадминтон или пинг-понг, как и на земле. Мяч или волан будет по отношению к стенам и полу перемещаться точно так же, как и по отношению к Земле при игре в обычных условиях. Если не посмотреть в окно, то с уверенностью нельзя сказать, что же происходит с поездом: движется он или стоит.<br> Если в движущемся с постоянной скоростью вагоне изучать падение тел, колебания маятника и другие явления, то результаты будут точно такими же, как и при исследовании этих явлений на Земле. Когда современный реактивный самолет летит со скоростью около 1000 км/ч, в его салоне не происходит ничего, что позволяло бы ощутить эту огромную скорость. Вы можете есть, спать, играть в шахматы, чувствуя себя как дома.<br> Лишь при резком торможении поезда нужно прилагать дополнительные усилия, чтобы устоять на ногах. При большой болтанке самолета или качке парохода на большой волне об игре с мячом не может быть и речи. Все предметы приходится закреплять, чтобы они оставались на своих местах.<br> '''Принцип относительности.''' На основании подобных наблюдений можно сформулировать один из самых фундаментальных законов природы - '''''принцип относительности:'''''<br> '''''Все механические процессы протекают одинаково во всех инерциальных системах отсчета.'''''<br> Это утверждение известно как принцип относительности в механике. Его еще называют принципом относительности Галилея.<br> Не нужно думать, что выполнение принципа относительности означает полную тождественность движения одного и того же тела относительно различных инерциальных систем отсчета. Тождественны лишь законы динамики. Законы движения тел определяются не только законами [[Элементы_релятивистской_динамики|динамики]], но и начальными скоростями и начальными координатами тел. А начальные скорости и начальные координаты данного тела относительно разных систем отсчета различны.<br> Так, камень будет падать отвесно, если его начальная скорость равна нулю по отношению к Земле. В равномерно движущемся поезде камень также будет падать отвесно по отношению к стенам вагона, если начальная скорость камня по отношению к поезду равна нулю. Но, с точки зрения наблюдателя на Земле, камень, падающий отвесно в поезде, будет двигаться по параболе (''рис.3.15, 3.16''). Дело в том, что начальная скорость камня по отношению к системе отсчета, связанной с Землей, отлична от нуля и равна скорости поезда.<br> |
| | | | |
| - | [[Image:A3.15.jpg|center|188x116px]][[Image:A3.16.jpg|center|330x139px]] Открытие принципа относительности - одно из величайших достижений человеческого разума. Оно оказалось возможным лишь после того, как люди поняли, что ни Земля, ни Солнце не являются центром Вселенной.<br> <br> | + | [[Image:A3.15.jpg|center|188x116px|мальчик]][[Image:A3.16.jpg|center|330x139px|Инерциальные системы отсчета]] Открытие принципа относительности - одно из величайших достижений человеческого разума. Оно оказалось возможным лишь после того, как люди поняли, что ни Земля, ни Солнце не являются центром [[Две_концепции_Вселенной|Вселенной]].<br> <br> |
| | | | |
| | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' | | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' |
| Строка 14: |
Строка 14: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | | | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 15:19, 4 июля 2012
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Инерциальные системы отсчета и принцип относительности в механике
Законы механики справедливы в инерциальных системах отсчета. Какие системы отсчета можно считать инерциальными?
Инерциальные и неинерциальные системы отсчета. Легко понять, что любая система отсчета, которая движется равномерно и прямолинейно относительно данной инерциальной системы отсчета, также является инерциальной. В самом деле, если тело относительно определенной инерциальной системы отсчета движется с постоянной скоростью 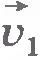 , то по отношению к системе отсчета, которая сама движется со скоростью , то по отношению к системе отсчета, которая сама движется со скоростью 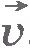 , это тело согласно закону сложения скоростей будет двигаться с некоторой новой, но также постоянной скоростью , это тело согласно закону сложения скоростей будет двигаться с некоторой новой, но также постоянной скоростью 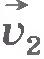 . .
Ускорение тела в обеих системах отсчета равно нулю.
Напротив, любая система отсчета, движущаяся с ускорением относительно инерциальной системы отсчета, уже будет неинерциальной. Действительно, если  , а скорость , а скорость 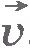 изменяется, то скорость изменяется, то скорость 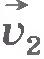 также будет меняться с течением времени: также будет меняться с течением времени: 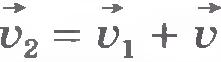 . .
Следовательно, характер движения тела будет изменяться при переходе от одной системы отсчета к другой.
Так как систему отсчета, связанную с Землей, можно приближенно рассматривать как инерциальную, то и системы отсчета, связанные с поездом, движущимся с постоянной скоростью, или с кораблем, плывущим по прямой с неизменной скоростью, также будут инерциальными. Но как только поезд начнет увеличивать свою скорость, связанная с ним система отсчета перестанет быть инерциальной. Закон инерции и второй закон Ньютона перестанут выполняться, если рассматривать движение по отношению к таким системам.
Геоцентрическая система отсчета инерциальна лишь приближенно. В действительности геоцентрическая система не является строго инерциальной. Наиболее близка к инерциальной система отсчета, связанная с Солнцем и неподвижными звездами. Земля же движется по отношению к этой системе отсчета с ускорением. Во-первых, она вращается вокруг своей оси и, во-вторых, движется по замкнутой орбите вокруг Солнца.
Ускорение, обусловленное обращением Земли вокруг Солнца, очень мало, так как велик период обращения (год). Значительно больше (примерно в 6 раз) ускорение, возникающее из-за вращения Земли вокруг оси с периодом Т = 24 ч. Но и оно невелико. На поверхности Земли у экватора, где это ускорение наибольшее, оно равно:
т. е. составляет всего 0,35% от ускорения свободного падения g=9,8 м/с2. Именно поэтому систему отсчета, связанную с Землей, можно приближенно рассматривать как инерциальную.
Доказательство вращения Земли. Однако существуют явления, которые нельзя объяснить, если считать геоцентрическую систему отсчета инерциальной. К ним относится вращение относительно Земли плоскости колебаний маятника в знаменитом опыте Фуко, доказывающем вращение Земли.
Рассмотрим колебания маятника в гелиоцентрической инерциальной системе отсчета. Для большей наглядности и простоты будем считать, что опыт проводится на полюсе.
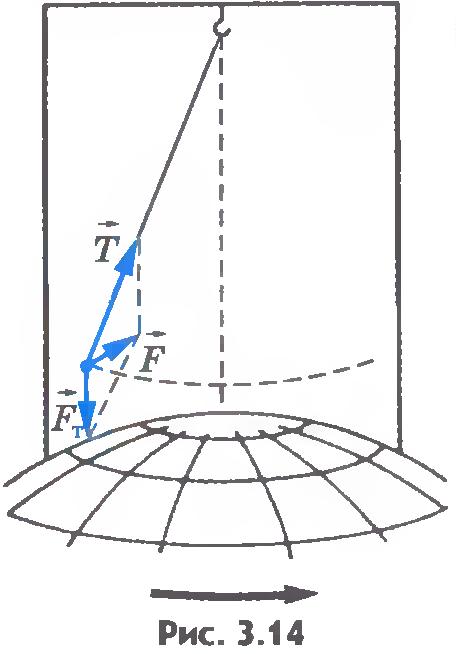
Пусть в начальный момент маятник отклоняют от положения равновесия. Действующие на маятник сила притяжения к Земле 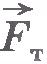 и сила упругости подвеса маятника и сила упругости подвеса маятника  лежат в той же вертикальной плоскости (рис.3.14). Согласно второму закону Ньютона ускорение маятника совпадает по направлению с равнодействующей силой лежат в той же вертикальной плоскости (рис.3.14). Согласно второму закону Ньютона ускорение маятника совпадает по направлению с равнодействующей силой  и поэтому лежит в той же вертикальной плоскости. А это значит, что с течением времени плоскость колебаний маятника в инерциальной системе отсчета должна оставаться неизменной. Так и происходит в гелиоцентрической системе. Однако система отсчета, связанная с Землей, не является инерциальной, и относительно нее плоскость колебаний маятника поворачивается вследствие вращения Земли. Чтобы это обнаружить, необходимо подвес сделать таким, чтобы трение в нем было мало, а сам маятник - достаточно массивным. Иначе трение в подвесе заставит плоскость колебаний следовать за вращением Земли. и поэтому лежит в той же вертикальной плоскости. А это значит, что с течением времени плоскость колебаний маятника в инерциальной системе отсчета должна оставаться неизменной. Так и происходит в гелиоцентрической системе. Однако система отсчета, связанная с Землей, не является инерциальной, и относительно нее плоскость колебаний маятника поворачивается вследствие вращения Земли. Чтобы это обнаружить, необходимо подвес сделать таким, чтобы трение в нем было мало, а сам маятник - достаточно массивным. Иначе трение в подвесе заставит плоскость колебаний следовать за вращением Земли.
Смещение плоскости колебаний маятника относительно Земли становится заметным уже через несколько минут. На средних широтах колебания маятника будут выглядеть несколько сложнее, но суть явления не изменится. Впервые такой опыт был произведен Ж. Фуко в 1850 г. в Париже.
Равномерное прямолинейное движение не влияет на механические процессы. Галилей первым обратил внимание на то, что равномерное прямолинейное движение по отношению к Земле совершенно не сказывается на течении всех механических явлений.
Допустим, вы находитесь в каюте корабля или в вагоне поезда, движущегося плавно, без толчков. Вы можете спокойно играть в бадминтон или пинг-понг, как и на земле. Мяч или волан будет по отношению к стенам и полу перемещаться точно так же, как и по отношению к Земле при игре в обычных условиях. Если не посмотреть в окно, то с уверенностью нельзя сказать, что же происходит с поездом: движется он или стоит.
Если в движущемся с постоянной скоростью вагоне изучать падение тел, колебания маятника и другие явления, то результаты будут точно такими же, как и при исследовании этих явлений на Земле. Когда современный реактивный самолет летит со скоростью около 1000 км/ч, в его салоне не происходит ничего, что позволяло бы ощутить эту огромную скорость. Вы можете есть, спать, играть в шахматы, чувствуя себя как дома.
Лишь при резком торможении поезда нужно прилагать дополнительные усилия, чтобы устоять на ногах. При большой болтанке самолета или качке парохода на большой волне об игре с мячом не может быть и речи. Все предметы приходится закреплять, чтобы они оставались на своих местах.
Принцип относительности. На основании подобных наблюдений можно сформулировать один из самых фундаментальных законов природы - принцип относительности:
Все механические процессы протекают одинаково во всех инерциальных системах отсчета.
Это утверждение известно как принцип относительности в механике. Его еще называют принципом относительности Галилея.
Не нужно думать, что выполнение принципа относительности означает полную тождественность движения одного и того же тела относительно различных инерциальных систем отсчета. Тождественны лишь законы динамики. Законы движения тел определяются не только законами динамики, но и начальными скоростями и начальными координатами тел. А начальные скорости и начальные координаты данного тела относительно разных систем отсчета различны.
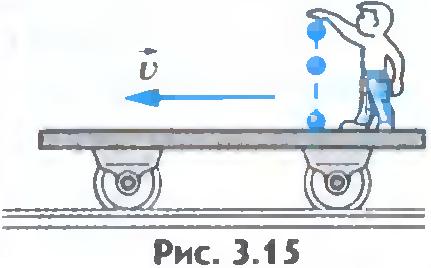
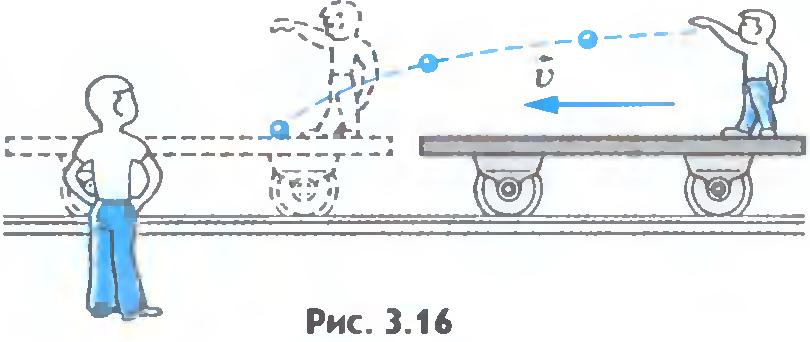
Так, камень будет падать отвесно, если его начальная скорость равна нулю по отношению к Земле. В равномерно движущемся поезде камень также будет падать отвесно по отношению к стенам вагона, если начальная скорость камня по отношению к поезду равна нулю. Но, с точки зрения наблюдателя на Земле, камень, падающий отвесно в поезде, будет двигаться по параболе (рис.3.15, 3.16). Дело в том, что начальная скорость камня по отношению к системе отсчета, связанной с Землей, отлична от нуля и равна скорости поезда.
Открытие принципа относительности - одно из величайших достижений человеческого разума. Оно оказалось возможным лишь после того, как люди поняли, что ни Земля, ни Солнце не являются центром Вселенной.
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Планирования по физике, учебники и книги онлайн, курсы и задания по физике для 10 класса
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|