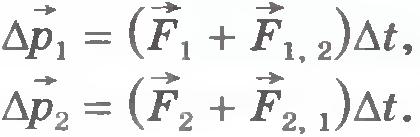|
|
|
| Строка 5: |
Строка 5: |
| | <metakeywords>Физика, 10 класс, Закон сохранения импульса</metakeywords> | | <metakeywords>Физика, 10 класс, Закон сохранения импульса</metakeywords> |
| | | | |
| - | Закон сохранения импульса является следствием второго и третьего законов Ньютона.<br> Для простоты будем считать, что система состоит всего из двух тел. Это могут быть две звезды, два бильярдных шара или два других тела.<br> Силы, возникающие в результате взаимодействия тела, принадлежащего системе, с телом, не принадлежащим ей, называются '''внешними силами'''. Если рассматривать систему, состоящую из двух бильярдных шаров, то сила взаимодействия шаров с краем стола при ударе о него, сила трения шара о поверхность стола - внешние силы. Пусть на тела системы действуют внешние силы [[Image:A40-10.jpg|21x30px]] и [[Image:A40-11.jpg|23x30px]].<br> Силы, возникающие в результате взаимодействия тел, принадлежащих системе, называются '''внутренними силами'''. Обозначим их через [[Image:A40-12.jpg|41x26px]] и [[Image:A40-13.jpg|34x26px]] (''рис.5.3''). <br>[[Image:A5.3.jpg|center|221x138px]]По третьему закону Ньютона [[Image:A40-14.jpg|101x26px]]. Отсюда следует, что сумма внутренних сил всегда равна нулю:<br>[[Image:A40-1.jpg|center|238x29px]] Вследствие действия сил на тела системы их импульсы изменяются. Если взаимодействие рассматривается за малый промежуток времени [[Image:A40-15.jpg|23x17px]], то для тел системы можно записать второй закон Ньютона в виде<br>[[Image:A40-2.jpg|center|184x60px]] Сложив эти равенства, получим<br>[[Image:A40-3.jpg|center|309x29px]] В левой части равенства (5.5) стоит сумма изменений импульсов всех тел системы, т. е. изменение импульса самой системы (под импульсом системы мы будем понимать геометрическую сумму импульсов всех тел системы):<br>[[Image:A40-4.jpg|center|278x29px]] Учитывая равенство (5.5), можно равенство (5.6) записать так:<br>[[Image:A40-5.jpg|center|403x28px]]где [[Image:A40-16.jpg|19x25px]] - геометрическая сумма всех внешних сил, действующих на тела системы.<br> Мы доказали весьма важное положение: '''импульс системы тел могут изменить только внешние силы, причем изменение импульса системы [[Image:A40-17.jpg|49x24px]] совпадает по направлению с суммарной внешней силой.''' Внутренние силы изменяют импульсы отдельных тел системы, но изменить суммарный импульс системы они не могут.<br> Уравнение (5.7) справедливо для любого интервала времени [[Image:A40-15.jpg|22x16px]], если сумма внешних сил остается постоянной.<br> Из уравнения (5.7) вытекает закон сохранения импульса. Если внешние силы на систему не действуют или их сумма равна нулю, то [[Image:A40-18.jpg|61x26px]] и импульс системы остается неизменным, или, как говорят, сохраняется:<br>[[Image:A40-6.jpg|center|344x41px]] '''''Закон сохранения импульса'''''формулируется так:'''''если сумма внешних сил равна нулю, то импульс системы тел сохраняется.''''' Иначе говоря, в этом случае тела могут только обмениваться импульсами, суммарное же значение импульса не изменяется.<br> Импульс, очевидно, сохраняется в изолированной системе тел, так как в этой системе на тела вообще не действуют внешние силы. Но область применения закона сохранения импульса шире: если даже на тела системы действуют внешние силы, но их сумма равна нулю (т. е. система является ''замкнутой''), то импульс системы все равно сохраняется.<br> Полученный результат справедлив для системы, содержащей произвольное число тел:<br>[[Image:A40-7.jpg|center|483x30px]]где [[Image:A40-8.jpg|143x32px]] - скорости тел в начальный момент времени; [[Image:A40-9.jpg|150x30px]] - скорости тел в конечный момент.<br> Так как импульс - векторная величина, то уравнение (5.9) представляет собой компактную запись трех уравнений для проекций импульсов системы на оси координат.<br> Если сумма внешних сил не равна нулю, но сумма проекций сил на какое-то направление равна нулю, то проекция суммарного импульса системы на это направление не меняется. Например, систему тел на Земле или вблизи поверхности Земли нельзя считать изолированной, так как на тела действует внешняя сила - сила тяжести. Однако вдоль горизонтального направления сила тяжести не действует и сумма проекций импульсов тел на это направление будет оставаться неизменной, если действием сил трения можно пренебречь.<br> В изолированной системе тел импульс системы сохраняется. Также он может сохраняться в случае, если сумма внешних сил, действующих на систему, равна нулю.<br><br><br> ???<br> 1. Сформулируйте закон сохранения импульса. <br> 2. В каких случаях можно применять закон сохранения импульса?<br> 3. В лежащий на гладком столе брусок попадает пуля, летящая горизонтально. Почему для нахождения скорости бруска с пулей можно применять закон сохранения импульса, хотя на брусок и пулю действуют внешние силы: сила тяжести, нормальная сила реакции стола?<br> | + | Закон сохранения импульса является следствием второго и [[Третий_закон_Ньютона|третьего законов Ньютона]].<br> Для простоты будем считать, что система состоит всего из двух тел. Это могут быть две звезды, два бильярдных шара или два других тела.<br> Силы, возникающие в результате взаимодействия тела, принадлежащего системе, с телом, не принадлежащим ей, называются '''внешними силами'''. Если рассматривать систему, состоящую из двух бильярдных шаров, то сила взаимодействия шаров с краем стола при ударе о него, сила трения шара о поверхность стола - внешние силы. Пусть на тела системы действуют внешние силы [[Image:A40-10.jpg|21x30px|A40-10.jpg]] и [[Image:A40-11.jpg|23x30px|A40-11.jpg]].<br> Силы, возникающие в результате взаимодействия тел, принадлежащих системе, называются '''внутренними силами'''. Обозначим их через [[Image:A40-12.jpg|41x26px|A40-12.jpg]] и [[Image:A40-13.jpg|34x26px|A40-13.jpg]] (''рис.5.3''). <br>[[Image:A5.3.jpg|center|221x138px|Закон сохранения импульса]]По третьему закону Ньютона [[Image:A40-14.jpg|101x26px|A40-14.jpg]]. Отсюда следует, что сумма внутренних сил всегда равна нулю:<br>[[Image:A40-1.jpg|center|238x29px|A40-1.jpg]] Вследствие действия сил на тела системы их импульсы изменяются. Если взаимодействие рассматривается за малый промежуток времени [[Image:A40-15.jpg|23x17px|A40-15.jpg]], то для тел системы можно записать [[Второй_закон_Ньютона._Масса|второй закон Ньютона]] в виде<br>[[Image:A40-2.jpg|center|184x60px|Закон сохранения импульса]] Сложив эти равенства, получим<br>[[Image:A40-3.jpg|center|309x29px|Закон сохранения импульса]] В левой части равенства (5.5) стоит сумма изменений импульсов всех тел системы, т. е. изменение импульса самой системы (под импульсом системы мы будем понимать геометрическую сумму импульсов всех тел системы):<br>[[Image:A40-4.jpg|center|278x29px|A40-4.jpg]] Учитывая равенство (5.5), можно равенство (5.6) записать так:<br>[[Image:A40-5.jpg|center|403x28px|Закон сохранения импульса]]где [[Image:A40-16.jpg|19x25px|A40-16.jpg]] - геометрическая сумма всех внешних сил, действующих на тела системы.<br> Мы доказали весьма важное положение: '''импульс системы тел могут изменить только внешние силы, причем изменение импульса системы [[Image:A40-17.jpg|49x24px|A40-17.jpg]] совпадает по направлению с суммарной внешней [[Роль_сил_трения|силой]].''' Внутренние силы изменяют импульсы отдельных тел системы, но изменить суммарный импульс системы они не могут.<br> Уравнение (5.7) справедливо для любого интервала времени [[Image:A40-15.jpg|22x16px|A40-15.jpg]], если сумма внешних сил остается постоянной.<br> Из уравнения (5.7) вытекает закон сохранения импульса. Если внешние силы на систему не действуют или их сумма равна нулю, то [[Image:A40-18.jpg|61x26px|A40-18.jpg]] и импульс системы остается неизменным, или, как говорят, сохраняется:<br>[[Image:A40-6.jpg|center|344x41px|Закон сохранения импульса]] '''''Закон сохранения импульса'''''формулируется так:'''''если сумма внешних сил равна нулю, то импульс системы тел сохраняется.''''' Иначе говоря, в этом случае тела могут только обмениваться импульсами, суммарное же значение импульса не изменяется.<br> Импульс, очевидно, сохраняется в изолированной системе тел, так как в этой системе на тела вообще не действуют внешние силы. Но область применения закона сохранения импульса шире: если даже на тела системы действуют внешние силы, но их сумма равна нулю (т. е. система является ''замкнутой''), то импульс системы все равно сохраняется.<br> Полученный результат справедлив для системы, содержащей произвольное число тел:<br>[[Image:A40-7.jpg|center|483x30px|Закон сохранения импульса]]где [[Image:A40-8.jpg|143x32px|A40-8.jpg]] - скорости тел в начальный момент времени; [[Image:A40-9.jpg|150x30px|A40-9.jpg]] - скорости тел в конечный момент.<br> Так как импульс - векторная величина, то уравнение (5.9) представляет собой компактную запись трех уравнений для проекций импульсов системы на [[Метод_координат|оси координат]].<br> Если сумма внешних сил не равна нулю, но сумма проекций сил на какое-то направление равна нулю, то проекция суммарного импульса системы на это направление не меняется. Например, систему тел на Земле или вблизи поверхности Земли нельзя считать изолированной, так как на тела действует внешняя сила - сила тяжести. Однако вдоль горизонтального направления сила тяжести не действует и сумма проекций импульсов тел на это направление будет оставаться неизменной, если действием сил трения можно пренебречь.<br> В изолированной системе тел импульс системы сохраняется. Также он может сохраняться в случае, если сумма внешних сил, действующих на систему, равна нулю.<br><br><br> ???<br> 1. Сформулируйте закон сохранения [[Импульс_материальной_точки._Другая_формулировка_второго_закона_Ньютона|импульса]]. <br> 2. В каких случаях можно применять закон сохранения импульса?<br> 3. В лежащий на гладком столе брусок попадает пуля, летящая горизонтально. Почему для нахождения скорости бруска с пулей можно применять закон сохранения импульса, хотя на брусок и пулю действуют внешние силы: сила тяжести, нормальная сила реакции стола?<br> |
| | | | |
| | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' | | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' |
| Строка 12: |
Строка 12: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | | | |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Версия 04:34, 5 июля 2012
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Закон сохранения импульса
Закон сохранения импульса является следствием второго и третьего законов Ньютона.
Для простоты будем считать, что система состоит всего из двух тел. Это могут быть две звезды, два бильярдных шара или два других тела.
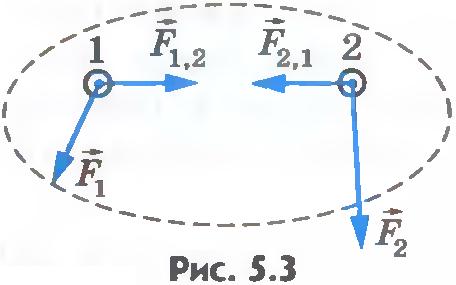
Силы, возникающие в результате взаимодействия тела, принадлежащего системе, с телом, не принадлежащим ей, называются внешними силами. Если рассматривать систему, состоящую из двух бильярдных шаров, то сила взаимодействия шаров с краем стола при ударе о него, сила трения шара о поверхность стола - внешние силы. Пусть на тела системы действуют внешние силы 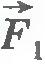 и и 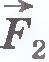 . .
Силы, возникающие в результате взаимодействия тел, принадлежащих системе, называются внутренними силами. Обозначим их через 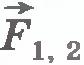 и и 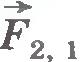 (рис.5.3). (рис.5.3).
По третьему закону Ньютона  . Отсюда следует, что сумма внутренних сил всегда равна нулю: . Отсюда следует, что сумма внутренних сил всегда равна нулю:
Вследствие действия сил на тела системы их импульсы изменяются. Если взаимодействие рассматривается за малый промежуток времени  , то для тел системы можно записать второй закон Ньютона в виде , то для тел системы можно записать второй закон Ньютона в виде
Сложив эти равенства, получим
В левой части равенства (5.5) стоит сумма изменений импульсов всех тел системы, т. е. изменение импульса самой системы (под импульсом системы мы будем понимать геометрическую сумму импульсов всех тел системы):
Учитывая равенство (5.5), можно равенство (5.6) записать так:
где  - геометрическая сумма всех внешних сил, действующих на тела системы. - геометрическая сумма всех внешних сил, действующих на тела системы.
Мы доказали весьма важное положение: импульс системы тел могут изменить только внешние силы, причем изменение импульса системы  совпадает по направлению с суммарной внешней силой. Внутренние силы изменяют импульсы отдельных тел системы, но изменить суммарный импульс системы они не могут. совпадает по направлению с суммарной внешней силой. Внутренние силы изменяют импульсы отдельных тел системы, но изменить суммарный импульс системы они не могут.
Уравнение (5.7) справедливо для любого интервала времени  , если сумма внешних сил остается постоянной. , если сумма внешних сил остается постоянной.
Из уравнения (5.7) вытекает закон сохранения импульса. Если внешние силы на систему не действуют или их сумма равна нулю, то 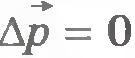 и импульс системы остается неизменным, или, как говорят, сохраняется: и импульс системы остается неизменным, или, как говорят, сохраняется:
Закон сохранения импульсаформулируется так:если сумма внешних сил равна нулю, то импульс системы тел сохраняется. Иначе говоря, в этом случае тела могут только обмениваться импульсами, суммарное же значение импульса не изменяется.
Импульс, очевидно, сохраняется в изолированной системе тел, так как в этой системе на тела вообще не действуют внешние силы. Но область применения закона сохранения импульса шире: если даже на тела системы действуют внешние силы, но их сумма равна нулю (т. е. система является замкнутой), то импульс системы все равно сохраняется.
Полученный результат справедлив для системы, содержащей произвольное число тел:
где 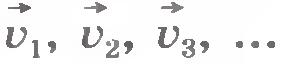 - скорости тел в начальный момент времени; - скорости тел в начальный момент времени; 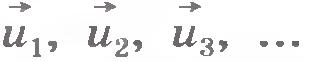 - скорости тел в конечный момент. - скорости тел в конечный момент.
Так как импульс - векторная величина, то уравнение (5.9) представляет собой компактную запись трех уравнений для проекций импульсов системы на оси координат.
Если сумма внешних сил не равна нулю, но сумма проекций сил на какое-то направление равна нулю, то проекция суммарного импульса системы на это направление не меняется. Например, систему тел на Земле или вблизи поверхности Земли нельзя считать изолированной, так как на тела действует внешняя сила - сила тяжести. Однако вдоль горизонтального направления сила тяжести не действует и сумма проекций импульсов тел на это направление будет оставаться неизменной, если действием сил трения можно пренебречь.
В изолированной системе тел импульс системы сохраняется. Также он может сохраняться в случае, если сумма внешних сил, действующих на систему, равна нулю.
???
1. Сформулируйте закон сохранения импульса.
2. В каких случаях можно применять закон сохранения импульса?
3. В лежащий на гладком столе брусок попадает пуля, летящая горизонтально. Почему для нахождения скорости бруска с пулей можно применять закон сохранения импульса, хотя на брусок и пулю действуют внешние силы: сила тяжести, нормальная сила реакции стола?
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Материалы по физике, задание и ответы по классам, планы конспектов уроков по физике для 10 класса
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|