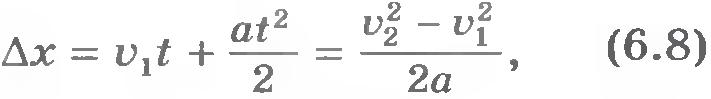|
|
|
| Строка 5: |
Строка 5: |
| | <metakeywords>Физика, 10 класс, Кинетическая энергия, и ее изменение</metakeywords> | | <metakeywords>Физика, 10 класс, Кинетическая энергия, и ее изменение</metakeywords> |
| | | | |
| - | В механике состояние системы определяется положением тел и их скоростями. Сначала выясним, как энергия тел зависит от их скоростей.<br> Подсчитаем работу постоянной силы [[Image:a46-9.jpg]], действующей на тело (материальную точку) массой ''m'' при его прямолинейном движении. Пусть направление силы совпадает с направлением скорости тела. В этом случае направления вектора перемещения [[Image:a46-10.jpg]] и вектора силы совпадают (''рис.6.4''). Поэтому работа силы [[Image:a46-9.jpg]] равна:<br>[[Image:a46-1.jpg|center]][[Image:a6.4.jpg|center]] Выберем координатную ось ''ОХ'' так, чтобы векторы [[Image:a46-11.jpg]] и [[Image:a46-10.jpg]] были направлены в сторону положительного направления этой оси. Тогда [[Image:a46-12.jpg]], и формулу для работы можно записать так: <br>[[Image:a46-2.jpg|center]] Согласно второму закону Ньютона<br>[[Image:a46-3.jpg|center]] Так как точка движется с постоянным ускорением, то изменение ее координаты [[Image:a46-13.jpg]] при переходе из начального положения в конечное можно найти по известной нам из кинематики формуле<br>[[Image:a46-4.jpg|center]]где<br>[[Image:a46-5.jpg|center]]Подставляя формулу (6.8) в формулу (6.6), получим<br>[[Image:a46-6.jpg|center]] Можно показать, что формула (6.9), выведенная для случая прямолинейного движения тела, на которое действует постоянная сила, справедлива и в тех случаях, когда на тело действует переменная сила и оно движется по криволинейной траектории.<br> Таким образом, работа силы при перемещении тела из начального положения в конечное равна изменению величины [[Image:a46-15.jpg]].<br> Величина [[Image:a46-15.jpg]] представляет собой энергию, которую имеет тело, движущееся со скоростью [[Image:a46-14.jpg]]. Эту энергию называют '''кинетической''' (от греческого слова «кинема» - движение).<br> Как видим, '''кинетическая энергия''' тела равна половине произведения массы тела на квадрат его скорости.<br> Будем обозначать кинетическую энергию буквой ''Е<sub>к</sub>'':<br>[[Image:a46-7.jpg|center]] Энергия измеряется, в тех же единицах, что и работа. Учитывая равенство (6.10), можно уравнение (6.9) записать так:<br>[[Image:a46-8.jpg|center]] Равенство (6.11) выражает теорему об изменении кинетической энергии: '''изменение кинетической энергии тела (материальной точки) за некоторый промежуток времени равно работе, совершенной за то же время силой, действующей на тело.''' Если на тело действует несколько сил, то изменение его кинетической энергии равно сумме работ всех сил, действующих на тело.<br> Кинетическая энергия тел зависит только от их масс и скоростей. Как мы увидим дальше, полная механическая энергия системы зависит от скоростей тел и расстояний между ними. Для того чтобы вычислить ту часть энергии, которая зависит от расстояний между телами, нужно предварительно рассмотреть вопрос о работе силы тяжести и силы упругости.<br> Движущееся тело обладает кинетической энергией. Эта энергия равна работе, которую надо совершить, чтобы увеличить скорость тела от нуля до значения ''v''.<br><br><br> ???<br> 1. Как выглядит график изменения кинетической энергии тела в зависимости от модуля его скорости? Начертите его.<br> 2. Какую работу совершила сила, действующая на тело, если направление его скорости изменилось на противоположное, а модуль ее остался без изменения?<br> 3. Три тела массами [[Image:a46-16.jpg]] имеют скорости [[Image:a46-17.jpg]], направленные под углом друг к другу. Запишите выражение для кинетической энергии системы этих трех тел.<br> 4. Зависит ли кинетическая энергия тела от выбора системы отсчета?<br> | + | В механике состояние системы определяется положением тел и их скоростями. Сначала выясним, как энергия тел зависит от их скоростей.<br> Подсчитаем работу постоянной силы [[Image:A46-9.jpg|16x24px]], действующей на тело (материальную точку) массой ''m'' при его прямолинейном движении. Пусть направление силы совпадает с направлением скорости тела. В этом случае направления вектора перемещения [[Image:A46-10.jpg|25x22px]] и вектора силы совпадают (''рис.6.4''). Поэтому работа силы [[Image:A46-9.jpg|16x24px]] равна:<br>[[Image:A46-1.jpg|center|94x23px]][[Image:A6.4.jpg|center|196x99px]] Выберем координатную ось ''ОХ'' так, чтобы векторы [[Image:A46-11.jpg|89x28px]] и [[Image:A46-10.jpg|26x22px]] были направлены в сторону положительного направления этой оси. Тогда [[Image:A46-12.jpg|86x21px]], и формулу для работы можно записать так: <br>[[Image:A46-2.jpg|center|195x20px]] Согласно второму закону Ньютона<br>[[Image:A46-3.jpg|center|174x21px]] Так как точка движется с постоянным ускорением, то изменение ее координаты [[Image:A46-13.jpg|27x17px]] при переходе из начального положения в конечное можно найти по известной нам из кинематики формуле<br>[[Image:A46-4.jpg|center|374x52px]]где<br>[[Image:A46-5.jpg|center|137x23px]]Подставляя формулу (6.8) в формулу (6.6), получим<br>[[Image:A46-6.jpg|center|391x47px]] Можно показать, что формула (6.9), выведенная для случая прямолинейного движения тела, на которое действует постоянная сила, справедлива и в тех случаях, когда на тело действует переменная сила и оно движется по криволинейной траектории.<br> Таким образом, работа силы при перемещении тела из начального положения в конечное равна изменению величины [[Image:A46-15.jpg|43x46px]].<br> Величина [[Image:A46-15.jpg|40x43px]] представляет собой энергию, которую имеет тело, движущееся со скоростью [[Image:A46-14.jpg|15x27px]]. Эту энергию называют '''кинетической''' (от греческого слова «кинема» - движение).<br> Как видим, '''кинетическая энергия''' тела равна половине произведения массы тела на квадрат его скорости.<br> Будем обозначать кинетическую энергию буквой ''Е<sub>к</sub>'':<br>[[Image:A46-7.jpg|center|250x62px]] Энергия измеряется, в тех же единицах, что и работа. Учитывая равенство (6.10), можно уравнение (6.9) записать так:<br>[[Image:A46-8.jpg|center|298x23px]] Равенство (6.11) выражает теорему об изменении кинетической энергии: '''изменение кинетической энергии тела (материальной точки) за некоторый промежуток времени равно работе, совершенной за то же время силой, действующей на тело.''' Если на тело действует несколько сил, то изменение его кинетической энергии равно сумме работ всех сил, действующих на тело.<br> Кинетическая энергия тел зависит только от их масс и скоростей. Как мы увидим дальше, полная механическая энергия системы зависит от скоростей тел и расстояний между ними. Для того чтобы вычислить ту часть энергии, которая зависит от расстояний между телами, нужно предварительно рассмотреть вопрос о работе силы тяжести и силы упругости.<br> Движущееся тело обладает кинетической энергией. Эта энергия равна работе, которую надо совершить, чтобы увеличить скорость тела от нуля до значения ''v''.<br><br><br> ???<br> 1. Как выглядит график изменения кинетической энергии тела в зависимости от модуля его скорости? Начертите его.<br> 2. Какую работу совершила сила, действующая на тело, если направление его скорости изменилось на противоположное, а модуль ее остался без изменения?<br> 3. Три тела массами [[Image:A46-16.jpg|102x19px]] имеют скорости [[Image:A46-17.jpg|88x20px]], направленные под углом друг к другу. Запишите выражение для кинетической энергии системы этих трех тел.<br> 4. Зависит ли кинетическая энергия тела от выбора системы отсчета?<br> |
| | | | |
| - | | + | <br> ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' |
| - | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' | + | |
| | | | |
| | <br> <sub>Материалы [[Физика и астрономия|по физике]], задание и ответы по классам, планы конспектов уроков [[Физика 10 класс|по физике для 10 класса]]</sub> | | <br> <sub>Материалы [[Физика и астрономия|по физике]], задание и ответы по классам, планы конспектов уроков [[Физика 10 класс|по физике для 10 класса]]</sub> |
Версия 21:56, 16 августа 2010
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Кинетическая энергия и ее изменение
В механике состояние системы определяется положением тел и их скоростями. Сначала выясним, как энергия тел зависит от их скоростей.
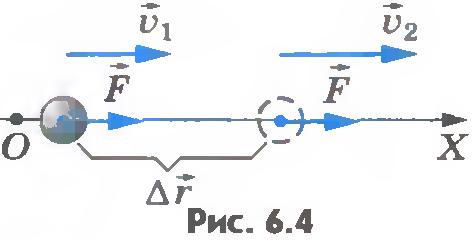
Подсчитаем работу постоянной силы 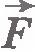 , действующей на тело (материальную точку) массой m при его прямолинейном движении. Пусть направление силы совпадает с направлением скорости тела. В этом случае направления вектора перемещения , действующей на тело (материальную точку) массой m при его прямолинейном движении. Пусть направление силы совпадает с направлением скорости тела. В этом случае направления вектора перемещения 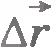 и вектора силы совпадают (рис.6.4). Поэтому работа силы и вектора силы совпадают (рис.6.4). Поэтому работа силы 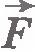 равна: равна:
Выберем координатную ось ОХ так, чтобы векторы 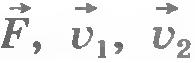 и и 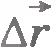 были направлены в сторону положительного направления этой оси. Тогда были направлены в сторону положительного направления этой оси. Тогда  , и формулу для работы можно записать так: , и формулу для работы можно записать так:
Согласно второму закону Ньютона
Так как точка движется с постоянным ускорением, то изменение ее координаты  при переходе из начального положения в конечное можно найти по известной нам из кинематики формуле при переходе из начального положения в конечное можно найти по известной нам из кинематики формуле
где
Подставляя формулу (6.8) в формулу (6.6), получим
Можно показать, что формула (6.9), выведенная для случая прямолинейного движения тела, на которое действует постоянная сила, справедлива и в тех случаях, когда на тело действует переменная сила и оно движется по криволинейной траектории.
Таким образом, работа силы при перемещении тела из начального положения в конечное равна изменению величины 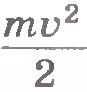 . .
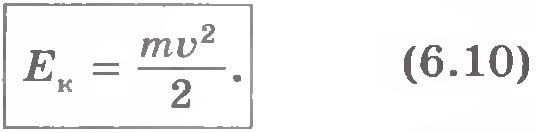
Величина 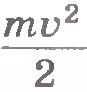 представляет собой энергию, которую имеет тело, движущееся со скоростью представляет собой энергию, которую имеет тело, движущееся со скоростью 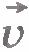 . Эту энергию называют кинетической (от греческого слова «кинема» - движение). . Эту энергию называют кинетической (от греческого слова «кинема» - движение).
Как видим, кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости.
Будем обозначать кинетическую энергию буквой Ек:
Энергия измеряется, в тех же единицах, что и работа. Учитывая равенство (6.10), можно уравнение (6.9) записать так:
Равенство (6.11) выражает теорему об изменении кинетической энергии: изменение кинетической энергии тела (материальной точки) за некоторый промежуток времени равно работе, совершенной за то же время силой, действующей на тело. Если на тело действует несколько сил, то изменение его кинетической энергии равно сумме работ всех сил, действующих на тело.
Кинетическая энергия тел зависит только от их масс и скоростей. Как мы увидим дальше, полная механическая энергия системы зависит от скоростей тел и расстояний между ними. Для того чтобы вычислить ту часть энергии, которая зависит от расстояний между телами, нужно предварительно рассмотреть вопрос о работе силы тяжести и силы упругости.
Движущееся тело обладает кинетической энергией. Эта энергия равна работе, которую надо совершить, чтобы увеличить скорость тела от нуля до значения v.
???
1. Как выглядит график изменения кинетической энергии тела в зависимости от модуля его скорости? Начертите его.
2. Какую работу совершила сила, действующая на тело, если направление его скорости изменилось на противоположное, а модуль ее остался без изменения?
3. Три тела массами  имеют скорости имеют скорости  , направленные под углом друг к другу. Запишите выражение для кинетической энергии системы этих трех тел. , направленные под углом друг к другу. Запишите выражение для кинетической энергии системы этих трех тел.
4. Зависит ли кинетическая энергия тела от выбора системы отсчета?
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Материалы по физике, задание и ответы по классам, планы конспектов уроков по физике для 10 класса
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|