|
|
|
| Строка 5: |
Строка 5: |
| | <metakeywords>Физика, 10 класс, Работа силы упругости</metakeywords> | | <metakeywords>Физика, 10 класс, Работа силы упругости</metakeywords> |
| | | | |
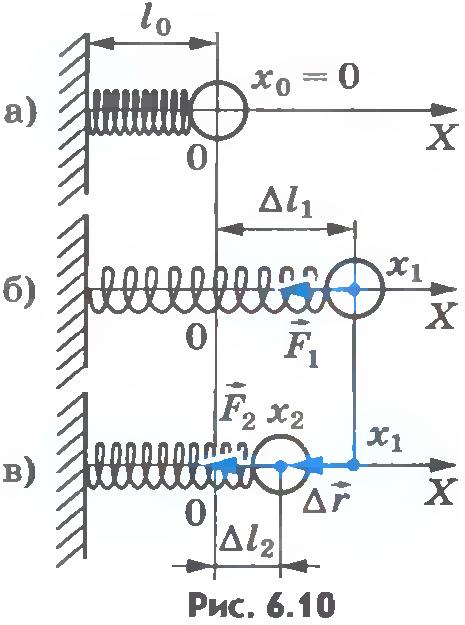
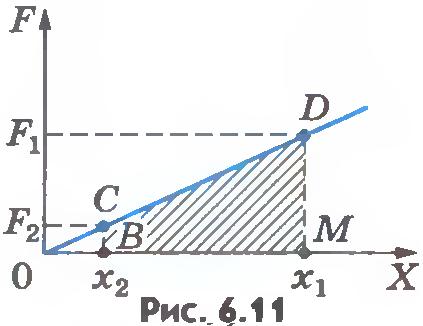
| - | Подобно силе тяжести, сила упругости тоже является консервативной. Чтобы убедиться в этом, вычислим работу, которую совершает пружина при перемещении груза.<br> На рисунке 6.10, а показана пружина, у которой один конец закреплен неподвижно, а к другому концу прикреплен шар. Если пружина растянута, то она действует на шар с силой [[Image:a48-7.jpg]] (''рис.6.10,б''), направленной к положению равновесия шара, в котором пружина не деформирована. Начальное удлинение пружины равно [[Image:a48-8.jpg]]. Вычислим работу силы упругости при перемещении шара из точки с координатой ''x<sub>1</sub>'' в точку с координатой ''x<sub>2</sub>''. Из рисунка 6.10, в видно, что модуль перемещения равен:<br>[[Image:a48-1.jpg|center]]где [[Image:a48-9.jpg]] - конечное удлинение пружины.<br>[[Image:a6.10.jpg|center]] Вычислить работу силы упругости по формуле (6.2) нельзя, так как эта формула справедлива лишь для постоянной силы, а сила упругости при изменении деформации пружины не остается постоянной. Для вычисления работы силы упругости воспользуемся графиком за¬висимости модуля силы упругости от координаты шара (''рис.6.11'').<br>[[Image:a6.11.jpg|center]] В § 43 мы показали, что при постоянном значении проекции силы на перемещение точки приложения силы ее работа может быть определена по графику зависимости ''F<sub>x</sub> ''от ''x'' и что эта работа численно равна площади прямоугольника. При произвольной зависимости ''F<sub>x</sub> ''от ''x'', разбивая перемещение на малые отрезки, в пределах каждого из которых силу можно считать постоянной, увидим, что работа будет численно равна площади трапеции.<br> В нашем примере работа силы упругости на перемещении точки ее приложения [[Image:a48-2.jpg]] численно равна площади трапеции ''ВCDM''. Следовательно,<br>[[Image:a48-3.jpg|center]] Согласно закону Гука [[Image:a48-10.jpg]] и [[Image:a48-11.jpg]]. Подставляя эти выражения для сил в уравнение (6.17) и учитывая, что [[Image:a48-.jpg]], получим<br>[[Image:a48-5.jpg|center]]Или окончательно<br>[[Image:a48-6.jpg|center]] Мы рассмотрели случай, когда направления силы упругости и перемещения тела совпадали: [[Image:a48-12.jpg]]. Но можно было бы найти работу силы упругости, когда ее направление противоположно перемещению тела или составляет с ним произвольный угол, а также при перемещении тела вдоль кривой произвольной формы.<br> Во всех этих случаях движения тела под действием силы упругости мы пришли бы к той же формуле для работы (6.18). Работа сил упругости зависит лишь от деформаций пружины [[Image:a48-8.jpg]] и [[Image:a48-9.jpg]] в начальном и конечном состояниях.<br> Таким образом, работа силы упругости не зависит от формы траектории и, так же как и сила тяжести, сила упругости является консервативной.<br><br><br> ???<br> 1. Чему равна работа силы упругости при перемещении тела по замкнутой траектории?<br> 2. Какие силы называют консервативными?<br> | + | Подобно силе тяжести, сила упругости тоже является консервативной. Чтобы убедиться в этом, вычислим работу, которую совершает пружина при перемещении груза.<br> На рисунке 6.10, а показана пружина, у которой один конец закреплен неподвижно, а к другому концу прикреплен шар. Если пружина растянута, то она действует на шар с силой [[Image:A48-7.jpg|18x24px]] (''рис.6.10,б''), направленной к положению равновесия шара, в котором пружина не деформирована. Начальное удлинение пружины равно [[Image:A48-8.jpg|25x20px]]. Вычислим работу силы упругости при перемещении шара из точки с координатой ''x<sub>1</sub>'' в точку с координатой ''x<sub>2</sub>''. Из рисунка 6.10, в видно, что модуль перемещения равен:<br>[[Image:A48-1.jpg|center|283x26px]]где [[Image:A48-9.jpg|25x18px]] - конечное удлинение пружины.<br>[[Image:A6.10.jpg|center|214x288px]] Вычислить работу силы упругости по формуле (6.2) нельзя, так как эта формула справедлива лишь для постоянной силы, а сила упругости при изменении деформации пружины не остается постоянной. Для вычисления работы силы упругости воспользуемся графиком за¬висимости модуля силы упругости от координаты шара (''рис.6.11'').<br>[[Image:A6.11.jpg|center|182x140px]] В § 43 мы показали, что при постоянном значении проекции силы на перемещение точки приложения силы ее работа может быть определена по графику зависимости ''F<sub>x</sub> ''от ''x'' и что эта работа численно равна площади прямоугольника. При произвольной зависимости ''F<sub>x</sub> ''от ''x'', разбивая перемещение на малые отрезки, в пределах каждого из которых силу можно считать постоянной, увидим, что работа будет численно равна площади трапеции.<br> В нашем примере работа силы упругости на перемещении точки ее приложения [[Image:A48-2.jpg|121x25px]] численно равна площади трапеции ''ВCDM''. Следовательно,<br>[[Image:A48-3.jpg|center|347x34px]] Согласно закону Гука [[Image:A48-10.jpg|80x19px]] и [[Image:A48-11.jpg|87x20px]]. Подставляя эти выражения для сил в уравнение (6.17) и учитывая, что [[Image:A48-.jpg|134x25px]], получим<br>[[Image:A48-5.jpg|center|396x45px]]Или окончательно<br>[[Image:A48-6.jpg|center|270x40px]] Мы рассмотрели случай, когда направления силы упругости и перемещения тела совпадали: [[Image:A48-12.jpg|143x20px]]. Но можно было бы найти работу силы упругости, когда ее направление противоположно перемещению тела или составляет с ним произвольный угол, а также при перемещении тела вдоль кривой произвольной формы.<br> Во всех этих случаях движения тела под действием силы упругости мы пришли бы к той же формуле для работы (6.18). Работа сил упругости зависит лишь от деформаций пружины [[Image:A48-8.jpg|27x21px]] и [[Image:A48-9.jpg|29x21px]] в начальном и конечном состояниях.<br> Таким образом, работа силы упругости не зависит от формы траектории и, так же как и сила тяжести, сила упругости является консервативной.<br><br><br> ???<br> 1. Чему равна работа силы упругости при перемещении тела по замкнутой траектории?<br> 2. Какие силы называют консервативными?<br> |
| | | | |
| - | | + | <br> ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' |
| - | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' | + | |
| | | | |
| | <br> | | <br> |
Версия 23:36, 16 августа 2010
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Работа силы упругости
Подобно силе тяжести, сила упругости тоже является консервативной. Чтобы убедиться в этом, вычислим работу, которую совершает пружина при перемещении груза.
На рисунке 6.10, а показана пружина, у которой один конец закреплен неподвижно, а к другому концу прикреплен шар. Если пружина растянута, то она действует на шар с силой 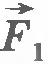 (рис.6.10,б), направленной к положению равновесия шара, в котором пружина не деформирована. Начальное удлинение пружины равно (рис.6.10,б), направленной к положению равновесия шара, в котором пружина не деформирована. Начальное удлинение пружины равно 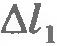 . Вычислим работу силы упругости при перемещении шара из точки с координатой x1 в точку с координатой x2. Из рисунка 6.10, в видно, что модуль перемещения равен: . Вычислим работу силы упругости при перемещении шара из точки с координатой x1 в точку с координатой x2. Из рисунка 6.10, в видно, что модуль перемещения равен:
где 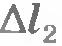 - конечное удлинение пружины. - конечное удлинение пружины.
Вычислить работу силы упругости по формуле (6.2) нельзя, так как эта формула справедлива лишь для постоянной силы, а сила упругости при изменении деформации пружины не остается постоянной. Для вычисления работы силы упругости воспользуемся графиком за¬висимости модуля силы упругости от координаты шара (рис.6.11).
В § 43 мы показали, что при постоянном значении проекции силы на перемещение точки приложения силы ее работа может быть определена по графику зависимости Fx от x и что эта работа численно равна площади прямоугольника. При произвольной зависимости Fx от x, разбивая перемещение на малые отрезки, в пределах каждого из которых силу можно считать постоянной, увидим, что работа будет численно равна площади трапеции.
В нашем примере работа силы упругости на перемещении точки ее приложения 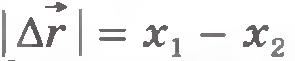 численно равна площади трапеции ВCDM. Следовательно, численно равна площади трапеции ВCDM. Следовательно,
Согласно закону Гука 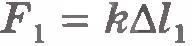 и и  . Подставляя эти выражения для сил в уравнение (6.17) и учитывая, что . Подставляя эти выражения для сил в уравнение (6.17) и учитывая, что 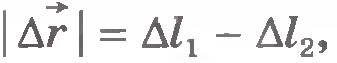 , получим , получим
Или окончательно
Мы рассмотрели случай, когда направления силы упругости и перемещения тела совпадали: 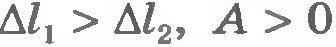 . Но можно было бы найти работу силы упругости, когда ее направление противоположно перемещению тела или составляет с ним произвольный угол, а также при перемещении тела вдоль кривой произвольной формы. . Но можно было бы найти работу силы упругости, когда ее направление противоположно перемещению тела или составляет с ним произвольный угол, а также при перемещении тела вдоль кривой произвольной формы.
Во всех этих случаях движения тела под действием силы упругости мы пришли бы к той же формуле для работы (6.18). Работа сил упругости зависит лишь от деформаций пружины 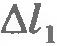 и и 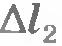 в начальном и конечном состояниях. в начальном и конечном состояниях.
Таким образом, работа силы упругости не зависит от формы траектории и, так же как и сила тяжести, сила упругости является консервативной.
???
1. Чему равна работа силы упругости при перемещении тела по замкнутой траектории?
2. Какие силы называют консервативными?
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Планирования по физике, учебники и книги онлайн, курсы и задания по физике для 10 класса
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|