|
|
|
| Строка 5: |
Строка 5: |
| | <metakeywords>Физика, 10 класс, Работа в термодинамике</metakeywords> | | <metakeywords>Физика, 10 класс, Работа в термодинамике</metakeywords> |
| | | | |
| - | В результате каких процессов может меняться внутренняя энергия? Вы уже знаете, что есть два вида таких процессов: совершение работы и теплопередача. Начнем с работы. Чему она равна при сжатии и расширении газа и других тел?<br> '''Работа в механике и термодинамике.''' В ''механике'' работа определяется как произведение модуля силы, модуля перемещения точки ее приложения и косинуса угла между ними. При действии силы на движущееся тело работа равна изменению его кинетической энергии.<br> В ''термодинамике'' движение тела как целого не рассматривается, речь идет о перемещении частей макроскопического тела друг относительно друга. В результате может меняться объем тела, а его скорость остается равной нулю. Работа в термодинамике определяется так же, как и в механике, но она равна не изменению кинетической энергии тела, а изменению его внутренней энергии.<br> '''Изменение внутренней энергии при совершении работы.''' Почему при сжатии или расширении тела меняется его внутренняя энергия тела? Почему, в частности, нагревается воздух при накачивании велосипедной шины?<br> Причина изменения температуры газа в процессе его сжатия состоит в следующем: ''при упругих соударениях молекул газа с движущимся поршнем изменяется их кинетическая энергия''. Так, при движении навстречу молекулам газа поршень во время столкновений передает им часть своей механической энергии, в результате чего газ нагревается. Поршень действует подобно футболисту, встречающему летящий мяч ударом ноги. Нога сообщает мячу скорость, значительно большую той, которой он обладал до удара.<br> И наоборот, если газ расширяется, то после столкновения с удаляющимся поршнем скорости молекул уменьшаются, в результате чего газ охлаждается. Так же действует и футболист, для того чтобы уменьшить скорость летящего мяча или остановить его, - нога футболиста движется от мяча, как бы уступая ему дорогу.<br> При сжатии или расширении меняется и средняя потенциальная энергия взаимодействия молекул, так как при этом меняется среднее расстояние между молекулами.<br> '''Вычисление работы.''' Вычислим работу в зависимости от изменения объема на примере газа в цилиндре под поршнем (''рис.13.1''). <br>[[Image:a13.1.jpg|center]]Проще всего вначале вычислить не работу силы [[Image:a76-5.jpg]], действующей на газ со стороны внешнего тела (поршня), а работу, которую совершает сила давления газа, действуя на поршень с силой [[Image:a76-6.jpg]]. Согласно третьему закону Ньютона [[Image:a76-7.jpg]]. Модуль силы, действующей со стороны газа на поршень, равен [[Image:a76-8.jpg]], где ''p'' - давление газа, а ''S'' - площадь поверхности поршня. Пусть газ расширяется изобарно и поршень смещается в направлении силы [[Image:a76-6.jpg]] на малое расстояние [[Image:a76-9.jpg]]. Так как давление газа постоянно, то работа газа равна:<br>[[Image:a76-1.jpg|center]] Эту работу можно выразить через изменение объема газа. Начальный его объем ''V<sub>1</sub>=Sh<sub>1</sub>'', а конечный ''V<sub>2</sub>=Sh<sub>2</sub>''. Поэтому<br>[[Image:a76-2.jpg|center]]где [[Image:a76-12.jpg]] - изменение объема газа.<br> При расширении газ совершает положительную работу, так как направление силы и направление перемещения поршня совпадают.<br> Если газ сжимается, то формула (13.3) для работы газа остается справедливой. Но теперь [[Image:a76-13.jpg]], и поэтому [[Image:a76-14.jpg]] (''рис.13.2'').<br>[[Image:a13.2.jpg|center]] Работа ''A'', совершаемая внешними телами над газом, отличается от работы самого газа ''A''´ только знаком: [[Image:a76-16.jpg]], так как сила [[Image:a76-5.jpg]], действующая на газ, направлена против силы [[Image:a76-6.jpg]] а перемещение поршня остается тем же самым. Поэтому работа внешних сил, действующих на газ, равна:<br>[[Image:a76-3.jpg|center]] При сжатии газа, когда [[Image:a76-17.jpg]], работа внешней силы оказывается положительной. Так и должно быть: при сжатии газа направления силы и перемещения точки ее приложения совпадают.<br> Если давление не поддерживать постоянным, то при расширении газ теряет энергию и передает ее окружающим телам: поднимающемуся поршню, воздуху и т. д. Газ при этом охлаждается. При сжатии газа, наоборот, внешние тела передают ему энергию и газ нагревается.<br> '''Геометрическое истолкование работы.''' Работе ''A´ ''газа для случая постоянного давления можно дать простое геометрическое истолкование.<br> Построим график зависимости давления газа от занимаемого им объема (''рис.13.3''). Здесь площадь прямоугольника ''abdc'', ограниченная графиком ''p<sub>1</sub>''=const, осью ''V'' и отрезками ''ab'' и ''cd'', равными давлению газа, численно равна работе (13.3):<br>[[Image:a76-4.jpg|center]][[Image:a13.3.jpg|center]] В общем случае давление газа не остается неизменным. Например, при изотермическом процессе оно убывает обратно пропорционально объему (''рис.13.4''). В этом случае для вычисления работы нужно разделить общее изменение объема на малые части и вычислить элементарные (малые) работы, а потом все их сложить. Работа газа по-прежнему численно равна площади фигуры, ограниченной графиком зависимости ''p'' от ''V'', осью ''V'' и отрезками ''ab'' и ''cd'', равными давлениям ''p<sub>1</sub>'', ''p<sub>2</sub>'' в начальном и конечном состояниях газа.<br>[[Image:a13.4.jpg|center]]<br><br> ???<br> 1. Почему газы при сжатии нагреваются?<br> 2. Положительную или отрицательную работу совершают внешние силы при изотермическом процессе, изображенном на рисунке 13.2?<br> | + | В результате каких процессов может меняться внутренняя энергия? Вы уже знаете, что есть два вида таких процессов: совершение работы и теплопередача. Начнем с работы. Чему она равна при сжатии и расширении газа и других тел?<br> '''Работа в механике и термодинамике.''' В ''механике'' работа определяется как произведение модуля силы, модуля перемещения точки ее приложения и косинуса угла между ними. При действии силы на движущееся тело работа равна изменению его кинетической энергии.<br> В ''термодинамике'' движение тела как целого не рассматривается, речь идет о перемещении частей макроскопического тела друг относительно друга. В результате может меняться объем тела, а его скорость остается равной нулю. Работа в термодинамике определяется так же, как и в механике, но она равна не изменению кинетической энергии тела, а изменению его внутренней энергии.<br> '''Изменение внутренней энергии при совершении работы.''' Почему при сжатии или расширении тела меняется его внутренняя энергия тела? Почему, в частности, нагревается воздух при накачивании велосипедной шины?<br> Причина изменения температуры газа в процессе его сжатия состоит в следующем: ''при упругих соударениях молекул газа с движущимся поршнем изменяется их кинетическая энергия''. Так, при движении навстречу молекулам газа поршень во время столкновений передает им часть своей механической энергии, в результате чего газ нагревается. Поршень действует подобно футболисту, встречающему летящий мяч ударом ноги. Нога сообщает мячу скорость, значительно большую той, которой он обладал до удара.<br> И наоборот, если газ расширяется, то после столкновения с удаляющимся поршнем скорости молекул уменьшаются, в результате чего газ охлаждается. Так же действует и футболист, для того чтобы уменьшить скорость летящего мяча или остановить его, - нога футболиста движется от мяча, как бы уступая ему дорогу.<br> При сжатии или расширении меняется и средняя потенциальная энергия взаимодействия молекул, так как при этом меняется среднее расстояние между молекулами.<br> '''Вычисление работы.''' Вычислим работу в зависимости от изменения объема на примере газа в цилиндре под поршнем (''рис.13.1''). <br>[[Image:A13.1.jpg|center|182x217px]]Проще всего вначале вычислить не работу силы [[Image:A76-5.jpg|14x21px]], действующей на газ со стороны внешнего тела (поршня), а работу, которую совершает сила давления газа, действуя на поршень с силой [[Image:A76-6.jpg|22x25px]]. Согласно третьему закону Ньютона [[Image:A76-7.jpg|60x20px]]. Модуль силы, действующей со стороны газа на поршень, равен [[Image:A76-8.jpg|66x20px]], где ''p'' - давление газа, а ''S'' - площадь поверхности поршня. Пусть газ расширяется изобарно и поршень смещается в направлении силы [[Image:A76-6.jpg|19x22px]] на малое расстояние [[Image:A76-9.jpg|113x20px]]. Так как давление газа постоянно, то работа газа равна:<br>[[Image:A76-1.jpg|center|441x20px]] Эту работу можно выразить через изменение объема газа. Начальный его объем ''V<sub>1</sub>=Sh<sub>1</sub>'', а конечный ''V<sub>2</sub>=Sh<sub>2</sub>''. Поэтому<br>[[Image:A76-2.jpg|center|269x19px]]где [[Image:A76-12.jpg|104x17px]] - изменение объема газа.<br> При расширении газ совершает положительную работу, так как направление силы и направление перемещения поршня совпадают.<br> Если газ сжимается, то формула (13.3) для работы газа остается справедливой. Но теперь [[Image:A76-13.jpg|57x17px]], и поэтому [[Image:A76-14.jpg|52x14px]] (''рис.13.2'').<br>[[Image:A13.2.jpg|center|192x212px]] Работа ''A'', совершаемая внешними телами над газом, отличается от работы самого газа ''A''´ только знаком: [[Image:A76-16.jpg|69x14px]], так как сила [[Image:A76-5.jpg|16x24px]], действующая на газ, направлена против силы [[Image:A76-6.jpg|21x24px]] а перемещение поршня остается тем же самым. Поэтому работа внешних сил, действующих на газ, равна:<br>[[Image:A76-3.jpg|center|233x30px]] При сжатии газа, когда [[Image:A76-17.jpg|135x18px]], работа внешней силы оказывается положительной. Так и должно быть: при сжатии газа направления силы и перемещения точки ее приложения совпадают.<br> Если давление не поддерживать постоянным, то при расширении газ теряет энергию и передает ее окружающим телам: поднимающемуся поршню, воздуху и т. д. Газ при этом охлаждается. При сжатии газа, наоборот, внешние тела передают ему энергию и газ нагревается.<br> '''Геометрическое истолкование работы.''' Работе ''A´ ''газа для случая постоянного давления можно дать простое геометрическое истолкование.<br> Построим график зависимости давления газа от занимаемого им объема (''рис.13.3''). Здесь площадь прямоугольника ''abdc'', ограниченная графиком ''p<sub>1</sub>''=const, осью ''V'' и отрезками ''ab'' и ''cd'', равными давлению газа, численно равна работе (13.3):<br>[[Image:A76-4.jpg|center|298x22px]][[Image:A13.3.jpg|center|250x181px]] В общем случае давление газа не остается неизменным. Например, при изотермическом процессе оно убывает обратно пропорционально объему (''рис.13.4''). В этом случае для вычисления работы нужно разделить общее изменение объема на малые части и вычислить элементарные (малые) работы, а потом все их сложить. Работа газа по-прежнему численно равна площади фигуры, ограниченной графиком зависимости ''p'' от ''V'', осью ''V'' и отрезками ''ab'' и ''cd'', равными давлениям ''p<sub>1</sub>'', ''p<sub>2</sub>'' в начальном и конечном состояниях газа.<br>[[Image:A13.4.jpg|center|253x180px]]<br><br> ???<br> 1. Почему газы при сжатии нагреваются?<br> 2. Положительную или отрицательную работу совершают внешние силы при изотермическом процессе, изображенном на рисунке 13.2?<br> |
| | | | |
| - | | + | <br> ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' |
| - | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' | + | |
| | | | |
| | <br> <sub>Планирования [[Физика и астрономия|по физике,]] учебники и книги онлайн, курсы и задания [[Физика 10 класс|по физике для 10 класса]]</sub> | | <br> <sub>Планирования [[Физика и астрономия|по физике,]] учебники и книги онлайн, курсы и задания [[Физика 10 класс|по физике для 10 класса]]</sub> |
Версия 17:52, 21 августа 2010
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Работа в термодинамике
В результате каких процессов может меняться внутренняя энергия? Вы уже знаете, что есть два вида таких процессов: совершение работы и теплопередача. Начнем с работы. Чему она равна при сжатии и расширении газа и других тел?
Работа в механике и термодинамике. В механике работа определяется как произведение модуля силы, модуля перемещения точки ее приложения и косинуса угла между ними. При действии силы на движущееся тело работа равна изменению его кинетической энергии.
В термодинамике движение тела как целого не рассматривается, речь идет о перемещении частей макроскопического тела друг относительно друга. В результате может меняться объем тела, а его скорость остается равной нулю. Работа в термодинамике определяется так же, как и в механике, но она равна не изменению кинетической энергии тела, а изменению его внутренней энергии.
Изменение внутренней энергии при совершении работы. Почему при сжатии или расширении тела меняется его внутренняя энергия тела? Почему, в частности, нагревается воздух при накачивании велосипедной шины?
Причина изменения температуры газа в процессе его сжатия состоит в следующем: при упругих соударениях молекул газа с движущимся поршнем изменяется их кинетическая энергия. Так, при движении навстречу молекулам газа поршень во время столкновений передает им часть своей механической энергии, в результате чего газ нагревается. Поршень действует подобно футболисту, встречающему летящий мяч ударом ноги. Нога сообщает мячу скорость, значительно большую той, которой он обладал до удара.
И наоборот, если газ расширяется, то после столкновения с удаляющимся поршнем скорости молекул уменьшаются, в результате чего газ охлаждается. Так же действует и футболист, для того чтобы уменьшить скорость летящего мяча или остановить его, - нога футболиста движется от мяча, как бы уступая ему дорогу.
При сжатии или расширении меняется и средняя потенциальная энергия взаимодействия молекул, так как при этом меняется среднее расстояние между молекулами.
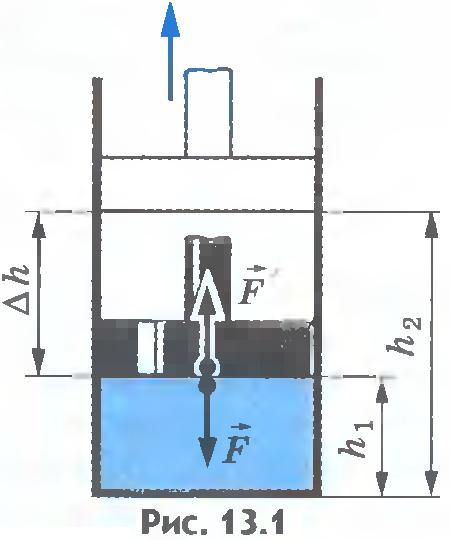
Вычисление работы. Вычислим работу в зависимости от изменения объема на примере газа в цилиндре под поршнем (рис.13.1).
Проще всего вначале вычислить не работу силы 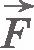 , действующей на газ со стороны внешнего тела (поршня), а работу, которую совершает сила давления газа, действуя на поршень с силой , действующей на газ со стороны внешнего тела (поршня), а работу, которую совершает сила давления газа, действуя на поршень с силой 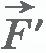 . Согласно третьему закону Ньютона . Согласно третьему закону Ньютона  . Модуль силы, действующей со стороны газа на поршень, равен . Модуль силы, действующей со стороны газа на поршень, равен 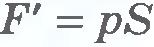 , где p - давление газа, а S - площадь поверхности поршня. Пусть газ расширяется изобарно и поршень смещается в направлении силы , где p - давление газа, а S - площадь поверхности поршня. Пусть газ расширяется изобарно и поршень смещается в направлении силы 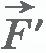 на малое расстояние на малое расстояние 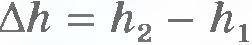 . Так как давление газа постоянно, то работа газа равна: . Так как давление газа постоянно, то работа газа равна:
Эту работу можно выразить через изменение объема газа. Начальный его объем V1=Sh1, а конечный V2=Sh2. Поэтому
где 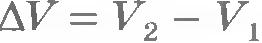 - изменение объема газа. - изменение объема газа.
При расширении газ совершает положительную работу, так как направление силы и направление перемещения поршня совпадают.
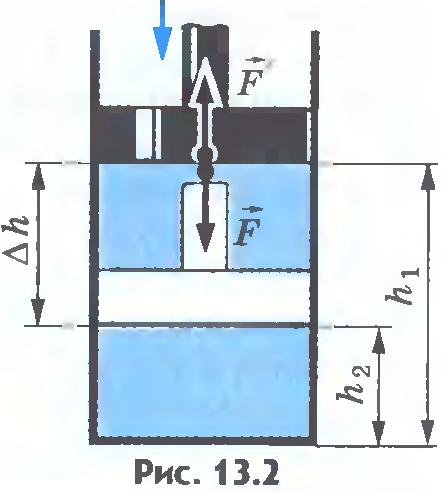
Если газ сжимается, то формула (13.3) для работы газа остается справедливой. Но теперь  , и поэтому , и поэтому  (рис.13.2). (рис.13.2).
Работа A, совершаемая внешними телами над газом, отличается от работы самого газа A´ только знаком:  , так как сила , так как сила 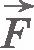 , действующая на газ, направлена против силы , действующая на газ, направлена против силы 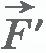 а перемещение поршня остается тем же самым. Поэтому работа внешних сил, действующих на газ, равна: а перемещение поршня остается тем же самым. Поэтому работа внешних сил, действующих на газ, равна:
При сжатии газа, когда  , работа внешней силы оказывается положительной. Так и должно быть: при сжатии газа направления силы и перемещения точки ее приложения совпадают. , работа внешней силы оказывается положительной. Так и должно быть: при сжатии газа направления силы и перемещения точки ее приложения совпадают.
Если давление не поддерживать постоянным, то при расширении газ теряет энергию и передает ее окружающим телам: поднимающемуся поршню, воздуху и т. д. Газ при этом охлаждается. При сжатии газа, наоборот, внешние тела передают ему энергию и газ нагревается.
Геометрическое истолкование работы. Работе A´ газа для случая постоянного давления можно дать простое геометрическое истолкование.
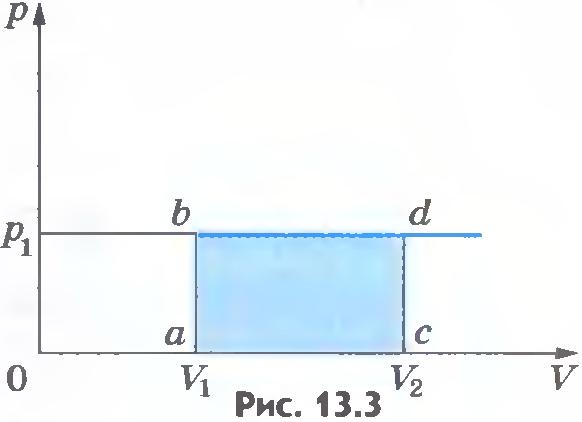
Построим график зависимости давления газа от занимаемого им объема (рис.13.3). Здесь площадь прямоугольника abdc, ограниченная графиком p1=const, осью V и отрезками ab и cd, равными давлению газа, численно равна работе (13.3):
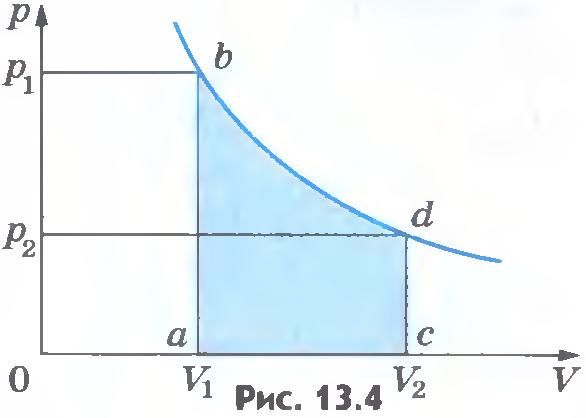
В общем случае давление газа не остается неизменным. Например, при изотермическом процессе оно убывает обратно пропорционально объему (рис.13.4). В этом случае для вычисления работы нужно разделить общее изменение объема на малые части и вычислить элементарные (малые) работы, а потом все их сложить. Работа газа по-прежнему численно равна площади фигуры, ограниченной графиком зависимости p от V, осью V и отрезками ab и cd, равными давлениям p1, p2 в начальном и конечном состояниях газа.
???
1. Почему газы при сжатии нагреваются?
2. Положительную или отрицательную работу совершают внешние силы при изотермическом процессе, изображенном на рисунке 13.2?
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Планирования по физике, учебники и книги онлайн, курсы и задания по физике для 10 класса
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|