|
|
|
| Строка 15: |
Строка 15: |
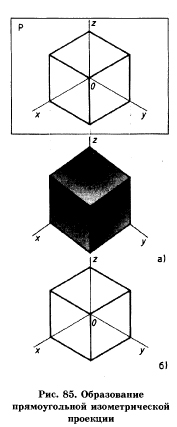
| | Рассмотрим, как получается прямоугольная изометрическая проекция (рис. 85). Поместив объект (в нашем примере куб) в координатный угол, расположим его с одинаковым наклоном граней К аксонометрической плоскоти проэкции.Через все точки объекта про¬ведем воображаемые параллельные проецирующие лучи под прямым углом к плоскости до пересечения с ней. Таким образом получим прямоугольную изометрическую проекцию куба и координатных осей.<br> | | Рассмотрим, как получается прямоугольная изометрическая проекция (рис. 85). Поместив объект (в нашем примере куб) в координатный угол, расположим его с одинаковым наклоном граней К аксонометрической плоскоти проэкции.Через все точки объекта про¬ведем воображаемые параллельные проецирующие лучи под прямым углом к плоскости до пересечения с ней. Таким образом получим прямоугольную изометрическую проекцию куба и координатных осей.<br> |
| | | | |
| - | [[Image:Черчн9.jpg|219x250px]] | + | [[Image:Черчн9.jpg|219x250px|Черчн9.jpg]] |
| | | | |
| | Координатные оси (х, у, z) отобразились на плоскости проекций расположенными под углом 120° друг к другу (рис. 87).<br> Для прямоугольной изометрической проекции коэффициенты искажения по всем трем осям х, у, z равны 1. Именно поэтому проекция была названа греческим словом «изометрия», что в переводе означает равное, одинаковое измерение (рис. 87). | | Координатные оси (х, у, z) отобразились на плоскости проекций расположенными под углом 120° друг к другу (рис. 87).<br> Для прямоугольной изометрической проекции коэффициенты искажения по всем трем осям х, у, z равны 1. Именно поэтому проекция была названа греческим словом «изометрия», что в переводе означает равное, одинаковое измерение (рис. 87). |
| | | | |
| - | [[Image:Черчн10.jpg|223x242px]]<br> | + | [[Image:Черчн10.jpg|223x242px|Черчн10.jpg]]<br> |
| | | | |
| - | При построении этой аксонометрической проекции по осям х, у, z (или линиям, параллельным им) откладывают действительные (натуральные) размеры длины, ширины и высоты предмета. | + | При построении этой аксонометрической проекции по осям х, у, z (или линиям, параллельным им) откладывают действительные (натуральные) размеры длины, ширины и высоты предмета. |
| | + | |
| | + | |
| | + | |
| | + | Н.А.Гордеенко, В.В.Степакова - Черчение.,9 класс<br>Отослано читателями из интернет-сайтов |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
Версия 13:39, 11 января 2011
Гипермаркет знаний>>Черчение 9 класс>>Черчение: Получение аксонометрических проекций
Рассмотрим процесс получения любой аксонометрической проекции. Перед аксонометрической плоскостью (плоскость, на которую проецируют) располагают предмет, помещенный в систему координатных осей (положение предмета относительно аксонометрической плоскости обусловлено выбором аксонометрической проекции). Затем задают направление проецирования (прямоугольное или косоугольное) и через все точки предмета мысленно проводят проецирующие лучи до пересечения с плоскостью проекции. Таким образом получают аксонометрические проекции (рис. 84, 85).
На аксонометрических проекциях форма предмета всегда передается одним изображением, позволяющим увидеть три его стороны.
Стандарт устанавливает несколько типов аксонометрических проекций. Познакомимся с двумя из них: косоугольной фронтальной диметрической проекцией (в ГОСТ 2.317-69 ее кратко называют фронтальной диметрической проекцией) и прямоугольной изометрической проекцией (сокращенный вариант названия — изометрическая проекция).
Получается косоугольная фронтальная диметрическая проекция следующим образом (рис. 84). Перед плоскостью Р располагают любой объект (например, куб) так, чтобы его передняя грань была параллельна плоскости проекций, т. е. фронтально. Параллельные между собой проецирующие лучи направляют под острым углом к плоскости Р. На аксонометрической плоскости проекций (Р) получают изображения координатных осей и косоугольную фронтальную диметрическую проекцию куба.
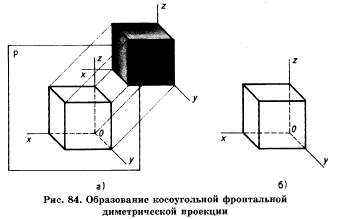
Координатные оси z и х отобразились на аксонометрическую плоскость проекции расположенными относительно друг друга под углом 90°. Ось х (продолжение оси) по отношению к оси у расположилась под углом 45° (рис. 86).
При выполнении любой аксонометрической проекции предметов пользуются коэффициентами искажения (КИ) по осям х, у, z. Для косоугольной фронтальной диметрической проекции коэффициенты искажения по осям х и z равны 1, а по оси у — 0,5. Удобство построения этой аксонометрической проекции состоит в том, что размеры длины и высоты предмета (отмеряемые по осям х и z либо по прямым, параллельным им) откладываются действительные (натуральные), а размеры ширины предмета (отмеряемые по оси у либо по прямым, параллельным ей) наносятся с уменьшением их величины в два раза.
Рассмотрим, как получается прямоугольная изометрическая проекция (рис. 85). Поместив объект (в нашем примере куб) в координатный угол, расположим его с одинаковым наклоном граней К аксонометрической плоскоти проэкции.Через все точки объекта про¬ведем воображаемые параллельные проецирующие лучи под прямым углом к плоскости до пересечения с ней. Таким образом получим прямоугольную изометрическую проекцию куба и координатных осей.

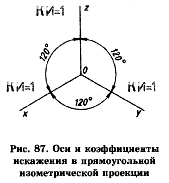
Координатные оси (х, у, z) отобразились на плоскости проекций расположенными под углом 120° друг к другу (рис. 87).
Для прямоугольной изометрической проекции коэффициенты искажения по всем трем осям х, у, z равны 1. Именно поэтому проекция была названа греческим словом «изометрия», что в переводе означает равное, одинаковое измерение (рис. 87).
При построении этой аксонометрической проекции по осям х, у, z (или линиям, параллельным им) откладывают действительные (натуральные) размеры длины, ширины и высоты предмета.
Н.А.Гордеенко, В.В.Степакова - Черчение.,9 класс
Отослано читателями из интернет-сайтов
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|














