|
|
|
| Строка 13: |
Строка 13: |
| | Построение аксонометрических проекций трапеции. Продолжим луч х за центр координат (т. О). От точки О по обе стороны на оси х откладываем отрезки, равные половине верхнего основания трапеции (по 20 мм). Во фронтальной диметрической проекции по оси у откладываем половину высоты трапеции (15 мм), а в изометрической проекции по той же оси откладываем отрезок, равный высоте трапеции. Через полученные засечки проводим отрезки прямых, параллельные оси х. На них по обе стороны от оси откладываем отрезки, равные половине нижнего основания трапеции. Полученные проекции вершин трапеции соединяем последовательно между собой и получаем аксонометрические проекции трапеции.<br> Построение аксонометрических проекций шестиугольника. От точки О в обе стороны по оси х откладываем отрезки, равные 25:2=12,5 мм. Через полученные засечки проводим прямые, параллельные оси у, и на них от оси х на прямых, параллельных оси у, откладываем отрезки, равные 1/4 стороны шестиугольника для фронтальной диметрической проекции и 1/2 стороны шестиугольника для прямоугольной изометрической проекции. Таким образом мы найдем четыре проекции вершин, принадлежащих шестиугольнику. По оси у от точки О во фронтальной диметрической проекции откладываем половину радиуса описанной окружности, а для изометрической проекции — величину К (радиус описанной окружности), получая еще две проекции вершин. Построенные проекции вершин последовательно соединяем, получая аксонометрическое изображение шестиугольника.<br> Рассмотрев построение аксонометрических проекций многоугольников, нетрудно заметить, что приемы получения их изображений во многом сходны как во фронтальной диметрической, так и в изометрической проекциях.<br> Примеры построения аксонометрии плоских фигур, вертикально расположенных в пространстве, рассмотрите самостоятельно по таблице 5. | | Построение аксонометрических проекций трапеции. Продолжим луч х за центр координат (т. О). От точки О по обе стороны на оси х откладываем отрезки, равные половине верхнего основания трапеции (по 20 мм). Во фронтальной диметрической проекции по оси у откладываем половину высоты трапеции (15 мм), а в изометрической проекции по той же оси откладываем отрезок, равный высоте трапеции. Через полученные засечки проводим отрезки прямых, параллельные оси х. На них по обе стороны от оси откладываем отрезки, равные половине нижнего основания трапеции. Полученные проекции вершин трапеции соединяем последовательно между собой и получаем аксонометрические проекции трапеции.<br> Построение аксонометрических проекций шестиугольника. От точки О в обе стороны по оси х откладываем отрезки, равные 25:2=12,5 мм. Через полученные засечки проводим прямые, параллельные оси у, и на них от оси х на прямых, параллельных оси у, откладываем отрезки, равные 1/4 стороны шестиугольника для фронтальной диметрической проекции и 1/2 стороны шестиугольника для прямоугольной изометрической проекции. Таким образом мы найдем четыре проекции вершин, принадлежащих шестиугольнику. По оси у от точки О во фронтальной диметрической проекции откладываем половину радиуса описанной окружности, а для изометрической проекции — величину К (радиус описанной окружности), получая еще две проекции вершин. Построенные проекции вершин последовательно соединяем, получая аксонометрическое изображение шестиугольника.<br> Рассмотрев построение аксонометрических проекций многоугольников, нетрудно заметить, что приемы получения их изображений во многом сходны как во фронтальной диметрической, так и в изометрической проекциях.<br> Примеры построения аксонометрии плоских фигур, вертикально расположенных в пространстве, рассмотрите самостоятельно по таблице 5. |
| | | | |
| - | <br>[[Image:Чер65.jpg|377x587px]] | + | <br>[[Image:Чер65.jpg|377x587px|Чер65.jpg]] |
| | | | |
| | <br> | | <br> |
| | | | |
| - | [[Image:Чер66.jpg|432x633px]] | + | [[Image:Чер66.jpg|432x633px|Чер66.jpg]] |
| | | | |
| | <br> | | <br> |
| | | | |
| - | '''Вопросы и задания'''<br>1. Какие проекции называются аксонометрическими?<br>2. В чем сходство аксонометрических проекций?<br>3. Чем отличается косоугольная фронтальная диметрическая проекция от прямоугольной изометрической проекции?<br>4. Какие коэффициенты искажения используются для построения косоугольной фронтальной диметрической проекции?<br>5. Какие коэффициенты искажения имеет прямоугольная изометрическая проекция?<br>6. В рабочей тетради постройте аксонометрические проекции (косоугольную фронтальную диметрическую и прямоугольную изометрическую проекции) правильного треугольника со сторонами, равными 30 мм, и шестиугольника со сторонами, равными 20 мм, расположив их в пространстве параллельно горизонтальной и фронтальной плоскостям проекций.<br><br>[[Image:Чер67.jpg|377x367px]]<br> | + | '''Вопросы и задания'''<br>1. Какие проекции называются аксонометрическими?<br>2. В чем сходство аксонометрических проекций?<br>3. Чем отличается косоугольная фронтальная диметрическая проекция от прямоугольной изометрической проекции?<br>4. Какие коэффициенты искажения используются для построения косоугольной фронтальной диметрической проекции?<br>5. Какие коэффициенты искажения имеет прямоугольная изометрическая проекция?<br>6. В рабочей тетради постройте аксонометрические проекции (косоугольную фронтальную диметрическую и прямоугольную изометрическую проекции) правильного треугольника со сторонами, равными 30 мм, и шестиугольника со сторонами, равными 20 мм, расположив их в пространстве параллельно горизонтальной и фронтальной плоскостям проекций.<br><br>[[Image:Чер67.jpg|377x367px|Чер67.jpg]]<br> |
| | | | |
| | + | <br> |
| | + | |
| | + | 7. Определите, в каких аксонометрических проекциях выполнены изображения проволочной модели, детали (рис. 89). |
| | + | |
| | + | 8. По наглядному изображению (рис. 90) постройте изометрическую проекцию детали, рассматривая ее форму как результат сложения или удаления нескольких призм.<br>9. На рис. 91 показаны модели, составленные из спичечных коробков (прямоугольных параллелепипедов). Сконструируйте новую форму модели, склейте ее из спичечных коробков. Постройте аксонометрическую проекцию (на выбор) своей модели.<br> |
| | | | |
| | | | |
| - | 7. Определите, в каких аксонометрических проекциях выполнены изображения проволочной модели, детали (рис. 89).
| |
| | | | |
| - | 8. По наглядному изображению (рис. 90) постройте изометрическую проекцию детали, рассматривая ее форму как результат сложения или удаления нескольких призм.<br>9. На рис. 91 показаны модели, составленные из спичечных коробков (прямоугольных параллелепипедов). Сконструируйте новую форму модели, склейте ее из спичечных коробков. Постройте аксонометрическую проекцию (на выбор) своей модели.<br>
| + | Н.А.Гордеенко, В.В.Степакова - Черчение.,9 класс<br>Отослано читателями из интернет-сайтов |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
Версия 13:40, 11 января 2011
Гипермаркет знаний>>Черчение 9 класс>>Черчение: Построение аксонометрических проекций
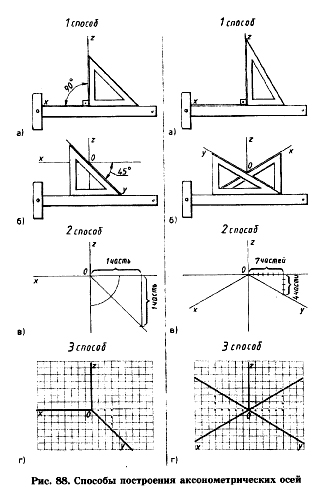
Аксонометрические проекции любого предмета начинают строить с осей. Различные способы построения осей фронтальной диметрической и изометрической проекций показаны на рис. 88.
Затем по осям или прямым, параллельным им, откладывают размеры изображаемого предмета и его элементов с учетом коэффициентов искажения. Соединяя изображения отдельных элементов формы соответствующим образом, получают аксонометрическую проекцию предмета.
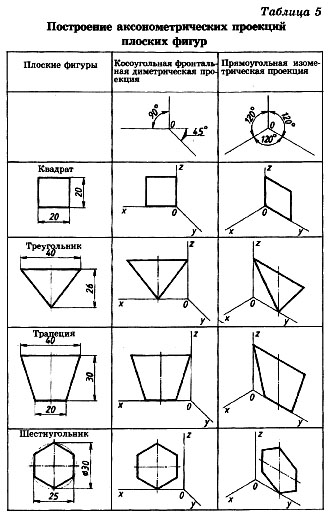
Построение плоских фигур в аксонометрических проекциях.Фигура, все точки которой находятся в одной плоскости, называется плоской. Примером плоских фигур могут служить треугольник, квадрат, прямоугольник, круг.
Знание приемов построения аксонометрических проекций плоских геометрических фигур (квадрата, треугольника, трапеции, шестиугольника) необходимо для построения аксонометрических проекций геометрических тел, моделей, деталей. Рассмотрим построение плоских фигур, лежащих в горизонтальной плоскости проекций (см. таблицу 4).
построение аксонометрической проекции квадрата. Сторону квадрата,равную 20 миллиметрам, откладываем вдоль оси х, поскольку коэффициент искажения по ней равен единице. Через засечку проводим прямую, параллельную оси у. Вдоль оси у во фронтальной диметрической проекции откладываем отрезок, равный величине стороны квадрата, умноженной на коэффициент искажения, то есть 20x0,5=10 мм.
На оси у в изометрической проекции откладываем размер стороны квадрата — 20 мм, так как коэффициент искажения по ней равен единице. Через полученные засечки проводим отрезки, параллельные оси х. Построили фронтальную диметрическую и изометрическую проекции квадрата.
Построение аксонометрических проекций треугольника. Продолжим луч х за точку начала координат (т. О). От точки О по обе стороны на оси х откладываем отрезки, равные половине стороны треугольника, получив тем самым изображение стороны треугольника. По оси у во фронтальной диметрической проекции откладываем половину высоты треугольника (26x0,5=13 мм), а в изометрической проекции по оси у откладываем размер, равный высоте треугольника (26 мм). Полученные засечки соединяем отрезками прямых, получая аксонометрические изображения треугольника.
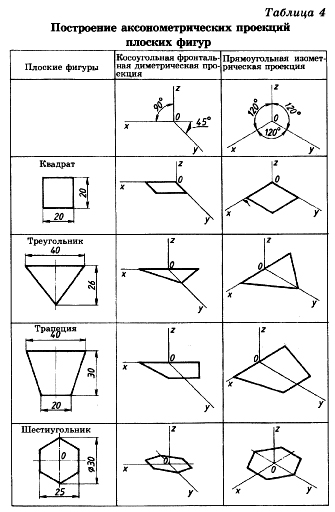
Построение аксонометрических проекций трапеции. Продолжим луч х за центр координат (т. О). От точки О по обе стороны на оси х откладываем отрезки, равные половине верхнего основания трапеции (по 20 мм). Во фронтальной диметрической проекции по оси у откладываем половину высоты трапеции (15 мм), а в изометрической проекции по той же оси откладываем отрезок, равный высоте трапеции. Через полученные засечки проводим отрезки прямых, параллельные оси х. На них по обе стороны от оси откладываем отрезки, равные половине нижнего основания трапеции. Полученные проекции вершин трапеции соединяем последовательно между собой и получаем аксонометрические проекции трапеции.
Построение аксонометрических проекций шестиугольника. От точки О в обе стороны по оси х откладываем отрезки, равные 25:2=12,5 мм. Через полученные засечки проводим прямые, параллельные оси у, и на них от оси х на прямых, параллельных оси у, откладываем отрезки, равные 1/4 стороны шестиугольника для фронтальной диметрической проекции и 1/2 стороны шестиугольника для прямоугольной изометрической проекции. Таким образом мы найдем четыре проекции вершин, принадлежащих шестиугольнику. По оси у от точки О во фронтальной диметрической проекции откладываем половину радиуса описанной окружности, а для изометрической проекции — величину К (радиус описанной окружности), получая еще две проекции вершин. Построенные проекции вершин последовательно соединяем, получая аксонометрическое изображение шестиугольника.
Рассмотрев построение аксонометрических проекций многоугольников, нетрудно заметить, что приемы получения их изображений во многом сходны как во фронтальной диметрической, так и в изометрической проекциях.
Примеры построения аксонометрии плоских фигур, вертикально расположенных в пространстве, рассмотрите самостоятельно по таблице 5.
Вопросы и задания
1. Какие проекции называются аксонометрическими?
2. В чем сходство аксонометрических проекций?
3. Чем отличается косоугольная фронтальная диметрическая проекция от прямоугольной изометрической проекции?
4. Какие коэффициенты искажения используются для построения косоугольной фронтальной диметрической проекции?
5. Какие коэффициенты искажения имеет прямоугольная изометрическая проекция?
6. В рабочей тетради постройте аксонометрические проекции (косоугольную фронтальную диметрическую и прямоугольную изометрическую проекции) правильного треугольника со сторонами, равными 30 мм, и шестиугольника со сторонами, равными 20 мм, расположив их в пространстве параллельно горизонтальной и фронтальной плоскостям проекций.
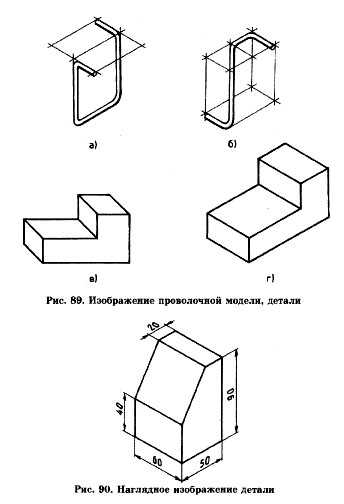
7. Определите, в каких аксонометрических проекциях выполнены изображения проволочной модели, детали (рис. 89).
8. По наглядному изображению (рис. 90) постройте изометрическую проекцию детали, рассматривая ее форму как результат сложения или удаления нескольких призм.
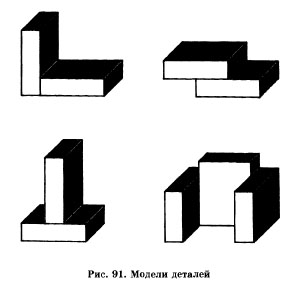
9. На рис. 91 показаны модели, составленные из спичечных коробков (прямоугольных параллелепипедов). Сконструируйте новую форму модели, склейте ее из спичечных коробков. Постройте аксонометрическую проекцию (на выбор) своей модели.
Н.А.Гордеенко, В.В.Степакова - Черчение.,9 класс
Отослано читателями из интернет-сайтов
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|















