|
|
|
| Строка 5: |
Строка 5: |
| | ''' ''' Для получения проекций плоских фигур достаточо спроецировать их вершины и затем последова тельно соединить одноименные проекции прямыми линиями, получив проекции фигуры.Для получения проекций криволинейных плоских фигур следует спроецировать ряд произвольных точек контура фигуры, затем соединить последовательно их одноименные проекции плавной замкнутой кривой, получив проекцию фигуры. | | ''' ''' Для получения проекций плоских фигур достаточо спроецировать их вершины и затем последова тельно соединить одноименные проекции прямыми линиями, получив проекции фигуры.Для получения проекций криволинейных плоских фигур следует спроецировать ряд произвольных точек контура фигуры, затем соединить последовательно их одноименные проекции плавной замкнутой кривой, получив проекцию фигуры. |
| | | | |
| - | [[Image:Черчн16.jpg|453x685px]]<br> Рассмотрим пример получения чертежа треугольника, который расположен в пространстве параллельно фронтальной плоскости проекции (таблица 10). Как видим, треугольник спроецировался на фронтальную плоскость проекций в натуральную величину. На горизонтальную и профильную плоскости проекций треугольник спроецировался в виде отрезков прямых.<br> Самостоятельно рассмотрите ортогональные чертежи плоских фигур, различным образом расположенных в пространстве (таблица 10).<br>'''Вывод:'''<br>1. Плоская фигура, расположенная параллельно какой-либо плоскости проекций, проецируется на эту плоскость без искажения.<br>2. Если плоская фигура перпендикулярна к какой-либо плоскости проекций, то она проецируется на эту плоскость отрезком прямой линии.<br>3. Если точка принадлежит плоской фигуре, то ее проекция соответственно принадлежит проекции плоской фигуры.<br><br>'''Вопросы и задания''' | + | [[Image:Черчн16.jpg|453x685px|Черчн16.jpg]]<br> Рассмотрим пример получения чертежа треугольника, который расположен в пространстве параллельно фронтальной плоскости проекции (таблица 10). Как видим, треугольник спроецировался на фронтальную плоскость проекций в натуральную величину. На горизонтальную и профильную плоскости проекций треугольник спроецировался в виде отрезков прямых.<br> Самостоятельно рассмотрите ортогональные чертежи плоских фигур, различным образом расположенных в пространстве (таблица 10).<br>'''Вывод:'''<br>1. Плоская фигура, расположенная параллельно какой-либо плоскости проекций, проецируется на эту плоскость без искажения.<br>2. Если плоская фигура перпендикулярна к какой-либо плоскости проекций, то она проецируется на эту плоскость отрезком прямой линии.<br>3. Если точка принадлежит плоской фигуре, то ее проекция соответственно принадлежит проекции плоской фигуры.<br><br>'''Вопросы и задания''' |
| | | | |
| - | 1. Как расположен прямоугольник относительно плоскостей проекций (рис. 117)<br>2. Выполните чертеж круга, расположенного параллельно фронтальной плоскости проекций.<br>[[Image:Черчн17.jpg|285x264px]] | + | 1. Как расположен прямоугольник относительно плоскостей проекций (рис. 117)<br>2. Выполните чертеж круга, расположенного параллельно фронтальной плоскости проекций.<br>[[Image:Черчн17.jpg|285x264px|Черчн17.jpg]] |
| | + | |
| | + | |
| | + | |
| | + | Н.А.Гордеенко, В.В.Степакова - Черчение.,9 класс<br>Отослано читателями из интернет-сайтов |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
Версия 13:43, 11 января 2011
Гипермаркет знаний>>Черчение 9 класс>>Черчение: Чертежи плоских фигур
Для получения проекций плоских фигур достаточо спроецировать их вершины и затем последова тельно соединить одноименные проекции прямыми линиями, получив проекции фигуры.Для получения проекций криволинейных плоских фигур следует спроецировать ряд произвольных точек контура фигуры, затем соединить последовательно их одноименные проекции плавной замкнутой кривой, получив проекцию фигуры.

Рассмотрим пример получения чертежа треугольника, который расположен в пространстве параллельно фронтальной плоскости проекции (таблица 10). Как видим, треугольник спроецировался на фронтальную плоскость проекций в натуральную величину. На горизонтальную и профильную плоскости проекций треугольник спроецировался в виде отрезков прямых.
Самостоятельно рассмотрите ортогональные чертежи плоских фигур, различным образом расположенных в пространстве (таблица 10).
Вывод:
1. Плоская фигура, расположенная параллельно какой-либо плоскости проекций, проецируется на эту плоскость без искажения.
2. Если плоская фигура перпендикулярна к какой-либо плоскости проекций, то она проецируется на эту плоскость отрезком прямой линии.
3. Если точка принадлежит плоской фигуре, то ее проекция соответственно принадлежит проекции плоской фигуры.
Вопросы и задания
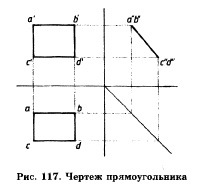
1. Как расположен прямоугольник относительно плоскостей проекций (рис. 117)
2. Выполните чертеж круга, расположенного параллельно фронтальной плоскости проекций.
Н.А.Гордеенко, В.В.Степакова - Черчение.,9 класс
Отослано читателями из интернет-сайтов
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|












