|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' § 1.8. Метод координат'''<br><br>«Лучше один раз увидеть, чем сто раз услышать», — гласит народная мудрость. Действительно, рисунки, схемы, чертежи и '''[[Растровая и векторная графика|графики]]''' способны заменить нам долгие разъяснения. | + | ''' § 1.8. Метод координат'''<br><br>«Лучше один раз увидеть, чем сто раз услышать», — гласит народная мудрость. Действительно, рисунки, схемы, чертежи и '''[[Растровая и векторная графика|графики]]''' способны заменить нам долгие разъяснения. |
| | | | |
| - | Любая, в том числе и графическая, '''[[Информация и знания|информация]]''' может быть представлена с помощью чисел. Чтобы «связать» числа и точки, используют системы координат. Простейшую из них - числовую ось вы уже рассматривали на уроках математики. | + | Любая, в том числе и графическая, '''[[Информация и знания|информация]]''' может быть представлена с помощью чисел. Чтобы «связать» числа и точки, используют системы координат. Простейшую из них - числовую ось вы уже рассматривали на уроках математики. |
| | | | |
| - | Мы с вами рассмотрим прямоугольную систему координат. Её также называют прямоугольной декартовой системой координат — в честь французского математика Рене Декарта. | + | Мы с вами рассмотрим прямоугольную систему координат. Её также называют прямоугольной декартовой системой координат — в честь французского математика Рене Декарта. |
| | | | |
| - | Нарисуем на листе в клетку две перпендикулярные оси, точку их пересечения обозначим через О.<br> <br>карт<br><br>Горизонтальная ось называется осью ОХ, вертикальная — осью OY. Место пересечения осей ОХ и OY называется началом координат, которое также обозначают цифрой 0 («ноль»). Каждая точка на координатной плоскости имеет свой точный адрес. Это пара чисел: первое число по оси ОХ, второе по оси ОУ. Эти числа называются координатами точки. А чтобы не путать порядок следования координат, вспомните, как устроены наши дома: сначала мы заходим в нужный подъезд (по оси ОХ), а затем поднимаемся на нужный этаж (по оси ОУ). <br> <br>карт<br><br>Посмотрите на шахматную доску. Вдоль её нижнего края идет ряд букв, а вдоль левого — ряд цифр. С их помощью можно однозначно определять положение любой фигуры на шахматной доске.<br> <br>карт<br><br>Оси координат разбивают плоскость на четыре части, которые называются координатными четвертями. Далее мы будем работать только в первой координатной четверти.<br><br>карт<br><br>'''Пример.''' Известны координаты пятнадцати точек:<br> <br>'''А(4, 1), В(4, 2), С(1, 2), Д(4, 5), Е(2, 5), F(4, 7), G(3, 7), H(5, 9), I(7, 7), J(6, 7), К(8, 5), L(6, 5), М(9, 2), N(6, 2), 0(6, 1). '''<br><br>Если отметить эти точки на координатной плоскости, а затем соединить их отрезками в последовательности А - В - С - D - Е — F -G - H - I - J - К - L - М - N — О - А, то получим следующий рисунок:<br><br>rfhn <br><br>Мы провели работу по декодированию графического изображения, состоящего из 15 соединённых отрезками точек, заданных с помощью декартовых прямоугольных координат. Другими словами, мы изменили форму представления информации с числовой на графическую. | + | Нарисуем на листе в клетку две перпендикулярные оси, точку их пересечения обозначим через О.<br> <br>[[Image:18-03-017.jpg]]<br><br>Горизонтальная ось называется осью ОХ, вертикальная — осью OY. Место пересечения осей ОХ и OY называется началом координат, которое также обозначают цифрой 0 («ноль»). Каждая точка на координатной плоскости имеет свой точный адрес. Это пара чисел: первое число по оси ОХ, второе по оси ОУ. Эти числа называются координатами точки. А чтобы не путать порядок следования координат, вспомните, как устроены наши дома: сначала мы заходим в нужный подъезд (по оси ОХ), а затем поднимаемся на нужный этаж (по оси ОУ). <br> <br>[[Image:18-03-018.jpg]]<br><br>Посмотрите на шахматную доску. Вдоль её нижнего края идет ряд букв, а вдоль левого — ряд цифр. С их помощью можно однозначно определять положение любой фигуры на шахматной доске.<br> <br>[[Image:18-03-019.jpg]]<br><br>Оси координат разбивают плоскость на четыре части, которые называются координатными четвертями. Далее мы будем работать только в первой координатной четверти.<br><br>[[Image:18-03-020.jpg]]<br><br>'''Пример.''' Известны координаты пятнадцати точек:<br> <br>'''А(4, 1), В(4, 2), С(1, 2), Д(4, 5), Е(2, 5), F(4, 7), G(3, 7), H(5, 9), I(7, 7), J(6, 7), К(8, 5), L(6, 5), М(9, 2), N(6, 2), 0(6, 1). '''<br><br>Если отметить эти точки на координатной плоскости, а затем соединить их отрезками в последовательности А - В - С - D - Е — F -G - H - I - J - К - L - М - N — О - А, то получим следующий рисунок:<br><br>[[Image:18-03-021.jpg]]<br><br>Мы провели работу по декодированию графического изображения, состоящего из 15 соединённых отрезками точек, заданных с помощью декартовых прямоугольных координат. Другими словами, мы изменили форму представления информации с числовой на графическую. |
| | | | |
| - | Об использовании метода координат в игре '''[[Игра «Морской бой» |Морской бой]]''' можно прочитать в § 3.7.<br><br>'''Самое главное'''<br><br>Рисунки, схемы, чертежи, графики — графические формы представления информации. Метод координат - это один из удобных способов представления графической информации с помощью чисел.<br>'''<br>Вопросы и задания'''<br><br>1. Что такое метод координат? Расскажите о нём.<br>2. Как метод координат применяется в географии?<br>3. Где вы сталкиваетесь с методом координат в быту?<br>4. Известны ли вам игры, основанные на методе координат? Об одной из таких игр можно прочесть в § 3.7.<br>5. На координатной плоскости отметьте и пронумеруйте точки со следующими координатами: <br>'''<br>А(2,5), В(6,5), С(11,7), D(11.4), Е(6,2), F(2,2), G(4,8), Н(9,9), I(3,2), J(3,4), К(5,4), L(5,2).'''<br><br>Соедините точки: <br><br>F — В — С — D — Е — F — А — G — Н — С. G - В - Е. I — J — К — L.<br><br>После проверки правильности выполнения задания можно раскрасить полученную картинку цветными карандашами. | + | Об использовании метода координат в игре '''[[Игра «Морской бой»|Морской бой]]''' можно прочитать в § 3.7.<br><br>'''Самое главное'''<br><br>Рисунки, схемы, чертежи, графики — графические формы представления информации. Метод координат - это один из удобных способов представления графической информации с помощью чисел.<br>'''<br>Вопросы и задания'''<br><br>1. Что такое метод координат? Расскажите о нём.<br>2. Как метод координат применяется в географии?<br>3. Где вы сталкиваетесь с методом координат в быту?<br>4. Известны ли вам игры, основанные на методе координат? Об одной из таких игр можно прочесть в § 3.7.<br>5. На координатной плоскости отметьте и пронумеруйте точки со следующими координатами: <br>'''<br>А(2,5), В(6,5), С(11,7), D(11.4), Е(6,2), F(2,2), G(4,8), Н(9,9), I(3,2), J(3,4), К(5,4), L(5,2).'''<br><br>Соедините точки: <br><br>F — В — С — D — Е — F — А — G — Н — С. G - В - Е. I — J — К — L.<br><br>После проверки правильности выполнения задания можно раскрасить полученную картинку цветными карандашами. |
| | | | |
| - | 6. Игра «Шифровальщик». Выполните действия по следующему плану: | + | 6. Игра «Шифровальщик». Выполните действия по следующему плану: |
| | | | |
| | 1) на листочке в клетку нарисуйте произвольный многоугольник;<br>2) пронумеруйте его вершины и закодируйте их с помощью координат:<br>3) задайте порядок соединения вершин;<br>1) проверьте, не допущена ли вами ошибка при кодировании рисунка;<br>5) координаты точек и порядок их соединения выпишите на отдельный листок;<br>6) предложите кому-нибудь восстановить ваш рисунок по этому коду;<br>7) сравните результаты — возможно искажение информации при декодировании.<br><br><br><br> | | 1) на листочке в клетку нарисуйте произвольный многоугольник;<br>2) пронумеруйте его вершины и закодируйте их с помощью координат:<br>3) задайте порядок соединения вершин;<br>1) проверьте, не допущена ли вами ошибка при кодировании рисунка;<br>5) координаты точек и порядок их соединения выпишите на отдельный листок;<br>6) предложите кому-нибудь восстановить ваш рисунок по этому коду;<br>7) сравните результаты — возможно искажение информации при декодировании.<br><br><br><br> |
Версия 18:57, 7 апреля 2012
Гипермаркет знаний>>Информатика >>Информатика 5 класс>> Метод координат
§ 1.8. Метод координат
«Лучше один раз увидеть, чем сто раз услышать», — гласит народная мудрость. Действительно, рисунки, схемы, чертежи и графики способны заменить нам долгие разъяснения.
Любая, в том числе и графическая, информация может быть представлена с помощью чисел. Чтобы «связать» числа и точки, используют системы координат. Простейшую из них - числовую ось вы уже рассматривали на уроках математики.
Мы с вами рассмотрим прямоугольную систему координат. Её также называют прямоугольной декартовой системой координат — в честь французского математика Рене Декарта.
Нарисуем на листе в клетку две перпендикулярные оси, точку их пересечения обозначим через О.
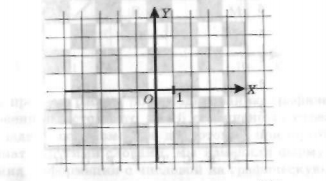
Горизонтальная ось называется осью ОХ, вертикальная — осью OY. Место пересечения осей ОХ и OY называется началом координат, которое также обозначают цифрой 0 («ноль»). Каждая точка на координатной плоскости имеет свой точный адрес. Это пара чисел: первое число по оси ОХ, второе по оси ОУ. Эти числа называются координатами точки. А чтобы не путать порядок следования координат, вспомните, как устроены наши дома: сначала мы заходим в нужный подъезд (по оси ОХ), а затем поднимаемся на нужный этаж (по оси ОУ).
Посмотрите на шахматную доску. Вдоль её нижнего края идет ряд букв, а вдоль левого — ряд цифр. С их помощью можно однозначно определять положение любой фигуры на шахматной доске.

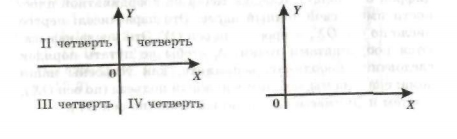
Оси координат разбивают плоскость на четыре части, которые называются координатными четвертями. Далее мы будем работать только в первой координатной четверти.
Пример. Известны координаты пятнадцати точек:
А(4, 1), В(4, 2), С(1, 2), Д(4, 5), Е(2, 5), F(4, 7), G(3, 7), H(5, 9), I(7, 7), J(6, 7), К(8, 5), L(6, 5), М(9, 2), N(6, 2), 0(6, 1).
Если отметить эти точки на координатной плоскости, а затем соединить их отрезками в последовательности А - В - С - D - Е — F -G - H - I - J - К - L - М - N — О - А, то получим следующий рисунок:
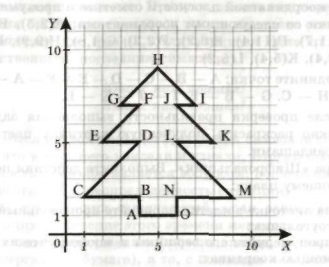
Мы провели работу по декодированию графического изображения, состоящего из 15 соединённых отрезками точек, заданных с помощью декартовых прямоугольных координат. Другими словами, мы изменили форму представления информации с числовой на графическую.
Об использовании метода координат в игре Морской бой можно прочитать в § 3.7.
Самое главное
Рисунки, схемы, чертежи, графики — графические формы представления информации. Метод координат - это один из удобных способов представления графической информации с помощью чисел.
Вопросы и задания
1. Что такое метод координат? Расскажите о нём.
2. Как метод координат применяется в географии?
3. Где вы сталкиваетесь с методом координат в быту?
4. Известны ли вам игры, основанные на методе координат? Об одной из таких игр можно прочесть в § 3.7.
5. На координатной плоскости отметьте и пронумеруйте точки со следующими координатами:
А(2,5), В(6,5), С(11,7), D(11.4), Е(6,2), F(2,2), G(4,8), Н(9,9), I(3,2), J(3,4), К(5,4), L(5,2).
Соедините точки:
F — В — С — D — Е — F — А — G — Н — С. G - В - Е. I — J — К — L.
После проверки правильности выполнения задания можно раскрасить полученную картинку цветными карандашами.
6. Игра «Шифровальщик». Выполните действия по следующему плану:
1) на листочке в клетку нарисуйте произвольный многоугольник;
2) пронумеруйте его вершины и закодируйте их с помощью координат:
3) задайте порядок соединения вершин;
1) проверьте, не допущена ли вами ошибка при кодировании рисунка;
5) координаты точек и порядок их соединения выпишите на отдельный листок;
6) предложите кому-нибудь восстановить ваш рисунок по этому коду;
7) сравните результаты — возможно искажение информации при декодировании.
Босова Л. Л., Информатика и ИКТ : учебник для 5 класса Л. Л. Босова. М. : БИНОМ. Лаборатория знаний, 2009. 192 с. : ил.
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|















