|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' 7.3. Сложность простых систем '''<br><br>Показателем сложности системы и её логической мощности может служить количество информационно-энергетических каналов связи (взаимодействия) с окружающей средой. В механике связи обычно ограничивают свободу передвижения некоторой части тела или отдельного объекта. Для высокоорганизованных систем, адаптирующихся к окружающей среде, наоборот, увеличение числа жающей среде, наоборот, увеличение числа связей - каналов восприятия информации - повышает свободу «маневра» системы или организма. При высокой сложности на передний план выступает не столько обмен энергией, сколько обмен информацией. Прием информации (при соответствующих затратах энергии) повышает упорядоченность системы, то есть эквивалентен уменьшению её энтропии. | + | ''' 7.3. Сложность простых систем '''<br><br>Показателем сложности системы и её логической мощности может служить количество информационно-энергетических каналов связи (взаимодействия) с окружающей средой. В механике связи обычно ограничивают свободу передвижения некоторой части тела или отдельного объекта. Для высокоорганизованных систем, адаптирующихся к окружающей среде, наоборот, увеличение числа жающей среде, наоборот, увеличение числа связей - каналов восприятия информации - повышает свободу «маневра» системы или организма. При высокой сложности на передний план выступает не столько обмен энергией, сколько обмен информацией. Прием информации (при соответствующих затратах энергии) повышает упорядоченность системы, то есть эквивалентен уменьшению её энтропии. |
| | | | |
| - | <br>[[Image:1-03-014.jpg]]<br><br>Отмечая это, мы должны иметь в виду, что сложное поведение некоторой системы может быть следствием достаточно простых законов, правил отбора, алгоритмов, на основе которых функционируют (работают, живут) технические системы или живые организмы.<br> <br>В предыдущем разделе мы привели примеры нелинейных зависимостей, неожиданно приводящих к динамическому хаосу. Здесь же уместно рассмотреть примеры того, как простые правила поведения элементов системы могут приводить к упорядоченным и достаточно сложным процессам кратного воспроизводства начальной конфигурации, направленным движениям и устойчивым структурам. Речь пойдет об эволюции состояний (движении состояний) в системах, где её одинаковые элементы взаимодействуют друг с другом, по крайней мере с ближайшими соседями. Элементами системы являются ячейки или клетки, которые могут находиться в двух состояниях: активном и пассивном, или включенном и выключенном, или живом и мертвом. Ячейки могут составлять правильные плоские или пространственные сети, примерами могут быть шахматная доска, лист тетради в клетку или экран компьютера, разделенный на квадратные или прямоугольные ячейки. <br><br>В 1960 г. Э. Фредкин (США) предложил вариант системы, в которой будущее состояние любой и каждой ячейки определяется текущим состоянием четырех ближайших соседей (расположенных к северу, востоку, югу и западу от выбранной). Ячейка, окруженная нечетным числом живых соседей, остается живой. Если число живых соседей четное, то ячейка умирает или остается мертвой. При таких законах жизни и смерти «клеток» любая начально заданная конфигурация колонии воспроизводится четырехкратно после определенного числа смены поколений. | + | <br>[[Image:1-03-014.jpg|мозг]]<br><br>Отмечая это, мы должны иметь в виду, что сложное поведение некоторой системы может быть следствием достаточно простых законов, правил отбора, [[Типы_алгоритмов|алгоритмов]], на основе которых функционируют (работают, живут) технические системы или живые организмы.<br> <br>В предыдущем разделе мы привели примеры нелинейных зависимостей, неожиданно приводящих к динамическому хаосу. Здесь же уместно рассмотреть примеры того, как простые правила поведения элементов системы могут приводить к упорядоченным и достаточно сложным процессам кратного воспроизводства начальной конфигурации, направленным движениям и устойчивым структурам. Речь пойдет об эволюции состояний (движении состояний) в системах, где её одинаковые элементы взаимодействуют друг с другом, по крайней мере с ближайшими соседями. Элементами системы являются ячейки или клетки, которые могут находиться в двух состояниях: активном и пассивном, или включенном и выключенном, или живом и мертвом. Ячейки могут составлять правильные плоские или пространственные сети, примерами могут быть шахматная доска, лист тетради в клетку или экран компьютера, разделенный на квадратные или прямоугольные ячейки. <br><br>В 1960 г. Э. Фредкин (США) предложил вариант системы, в которой будущее состояние любой и каждой ячейки определяется текущим состоянием четырех ближайших соседей (расположенных к северу, востоку, югу и западу от выбранной). Ячейка, окруженная нечетным числом живых соседей, остается живой. Если число живых соседей четное, то ячейка умирает или остается мертвой. При таких законах жизни и смерти «клеток» любая начально заданная конфигурация колонии воспроизводится четырехкратно после определенного числа смены поколений. |
| | | | |
| - | <br>[[Image:1-03-015.jpg]] <br> <br>Позже и сами копии учетверятся, и процесс размножения циклически продолжится, пока хватает клеточного поля. Периметр занятой колонией зоны расширяется, а её внутренняя область периодически то заполняется густой «порослью», то снова пустеет. <br><br>Вариант Э. Фредкина приводит к размножению копий начального формата и их расхождению, что создает иллюзию экспансии живых клеток. <br><br>Если учитывать большее число возможных связей, то поведение системы становится более сложным и менее предсказуемым заранее. В 1970 г. Дж. Конвэй (Великобритания) изобрел игру «Жизнь», в которой учитываются не 4, а 8 соседей каждой клетки (включая соседей второй координационной сферы, соединенных с выбранной клеткой по углам) [19]. Законы жизни и смерти установлены таким образом: живая клетка продолжит свое существование в следующем поколении лишь в тех случаях, когда в её окружении на данном этапе находятся две или три живых соседних ячейки. При меньшем числе живых соседей считается, что клетка умирает от одиночества, а при большем - от тесноты (стресса!). Для неживой клетки возрождение происходит только тогда, когда в её окружении будет ровно 3 живых ячейки. <br><br>В «Жизни» Конвэя движение состояний сильно зависит от формы начальной, зародышевой колонии клеток. Одна и две клетки сразу гибнут от одиночества, три клетки образуют стабильные циклические «мигалки», квадрат из четырех ячеек не изменяется. При большем числе исходных ячеек в колонии возникают разнообразные варианты: от быстрого вымирания до расходящихся и сближающихся «островов жизни», узоров или цветов (особенно если последующие поколения отмечаются своим цветом). В процессе движения состояний системы она может распадаться на стабильные циклические конфигурации и на направленно перемещающиеся по полю самовоспроизводящиеся фигуры, иногда довольно сложные. <br><br>После 30-го шага от начальной конфигурации (в центре), система выходит на цикл, представленный на рисунке. В нем постоянно живы красные и синие клетки. Желтые, зеленые, розовые - появляются циклически. <br><br>Практически невозможно описать возможные изменения начальных форм колоний или их эволюцию, лучше воспроизвести «Жизнь» в компьютерной лабораторной работе. Важно отметить, что увеличение числа связей с окружением - в данном случае переход от системы Фредкина к системе Конвэя - приводит к существенному усложнению получающихся в процессе движения состояний форм живых или активных элементов. Исходная простота оборачивается сложностью (геометрической формы активных элементов), устойчивостью (в циклах повторяющегося самовоспроизводства), кажущейся целенаправленностью (в случаях упорядоченного перемещения воспроизводящихся фигур) и принципиальной творческой потенцией (в смысле способности производства новых конфигураций). В ещё большей мере это проявляется в трехмерных компьютерных версиях «Жизни», когда число взаимодействующих соседей заметно возрастает. <br><br>[[Image:1-03-016.jpg]]<br><br>Рассмотренные игры являются, конечно, лишь отдаленной аналогией реальным процессам в окружающем мире (скорее, даже аллегорией). Однако такой видный основатель информатики как фон Нейман, всерьез доказал, что если каждая клетка имеет свой клеточный автомат (устройство), способный находиться в 29 состояниях, то при наличии сети из 200 тыс. ячеек информационно-логическая система (или Машина) способна самовоспроизвести свою копию (будучи помещенной в резервуар с необходимыми запасными частями и комплектующими). <br><br>Таким образом, в принципе возможна машинная эволюция, многократно обыгранная в научно-фантастических романах, где сталкиваются человеческая и машинная цивилизации или их представители. Нейрофизиологи обнаружили, что нейронные сети человеческого мозга во многом состоят из подобных по строению клеток, которые могут находиться в возбужденном или в заторможенном состояниях. Нейронные сообщества - участки коры мозга из нескольких сотен клеток, связанных между собой синаптическими связями, считаются единичными модулями коры. Было показано, что уже простые модельные нейронные сети, состояние ячейки которой зависит от силы воздействия соседей, способны создавать свои точные копии. <br><br>Более того, при циклическом и синхронном изменении порогов срабатывания нейронов (перехода между двумя состояниями) в связанных между собой модулях распространяются волны «обучения», когда модули воспроизводят в себе информацию, содержащуюся в соседнем участке (самовоспроизводят информацию), что проливает свет на процесс запоминания и распознавания образов человеком [18]. Самовоспроизведение и связанный с ним эффект образования однородных областей, состоящих из одинаковых нейронных сетей, естественным образом объясняет дифференциацию и специализацию различных участков мозга как результат спонтанной самоорганизации системы взаимодействующих нейросетей. <br><br>Общий вывод, который следует из приведенных примеров, состоит в том, что такие важнейшие свойства совместно эволюционирующих систем (Вселенная, звезды, жизнь на Земле и разум), как сложность, устойчивость, кажущаяся целенаправленность развития, могут быть следствием простых явлений, управляемых совокупностью общих законов. <br><br>Фактически в этом основа формирующейся эволюционно-синергетической парадигмы современного естествознания. В её рамках целью отдельных наук и научных направлений является поиск тех простых правил, которые и порождают изумительное разнообразие структур и форм в окружающем человека мире. <br><br><br><br><br>
| + | <br>[[Image:1-03-015.jpg|система Фредкина]] <br> <br>Позже и сами копии учетверятся, и процесс размножения циклически продолжится, пока хватает клеточного поля. Периметр занятой колонией зоны расширяется, а её внутренняя область периодически то заполняется густой «порослью», то снова пустеет. <br><br>Вариант Э. Фредкина приводит к размножению копий начального формата и их расхождению, что создает иллюзию экспансии живых клеток. <br><br>Если учитывать большее число возможных связей, то поведение системы становится более сложным и менее предсказуемым заранее. В 1970 г. Дж. Конвэй (Великобритания) изобрел игру «Жизнь», в которой учитываются не 4, а 8 соседей каждой клетки (включая соседей второй координационной сферы, соединенных с выбранной клеткой по углам) [19]. Законы жизни и смерти установлены таким образом: живая клетка продолжит свое существование в следующем поколении лишь в тех случаях, когда в её окружении на данном этапе находятся две или три живых соседних ячейки. При меньшем числе живых соседей считается, что клетка умирает от одиночества, а при большем - от тесноты (стресса!). Для неживой клетки возрождение происходит только тогда, когда в её окружении будет ровно 3 живых ячейки. <br><br>В «Жизни» Конвэя движение состояний сильно зависит от формы начальной, зародышевой колонии клеток. Одна и две клетки сразу гибнут от одиночества, три клетки образуют стабильные циклические «мигалки», квадрат из четырех ячеек не изменяется. При большем числе исходных ячеек в колонии возникают разнообразные варианты: от быстрого вымирания до расходящихся и сближающихся «островов жизни», узоров или цветов (особенно если последующие поколения отмечаются своим цветом). В процессе движения состояний системы она может распадаться на стабильные циклические конфигурации и на направленно перемещающиеся по полю самовоспроизводящиеся [[Геометрические_фигуры|фигуры]], иногда довольно сложные. <br><br>После 30-го шага от начальной конфигурации (в центре), система выходит на цикл, представленный на рисунке. В нем постоянно живы красные и синие клетки. Желтые, зеленые, розовые - появляются циклически. <br><br>Практически невозможно описать возможные изменения начальных форм колоний или их эволюцию, лучше воспроизвести «Жизнь» в компьютерной лабораторной работе. Важно отметить, что увеличение числа связей с окружением - в данном случае переход от системы Фредкина к системе Конвэя - приводит к существенному усложнению получающихся в процессе движения состояний форм живых или активных элементов. Исходная простота оборачивается сложностью (геометрической формы активных элементов), устойчивостью (в циклах повторяющегося самовоспроизводства), кажущейся целенаправленностью (в случаях упорядоченного перемещения воспроизводящихся фигур) и принципиальной творческой потенцией (в смысле способности производства новых [[Электронные_конфигурации_атомов_химических_элементов|конфигураций]]). В ещё большей мере это проявляется в трехмерных компьютерных версиях «Жизни», когда число взаимодействующих соседей заметно возрастает. <br><br>[[Image:1-03-016.jpg|конфигурация клеток]]<br><br>Рассмотренные игры являются, конечно, лишь отдаленной аналогией реальным процессам в окружающем мире (скорее, даже аллегорией). Однако такой видный основатель [[Методическая_поддержка_курса_информатики|информатики]] как фон Нейман, всерьез доказал, что если каждая клетка имеет свой клеточный автомат (устройство), способный находиться в 29 состояниях, то при наличии сети из 200 тыс. ячеек информационно-логическая система (или Машина) способна самовоспроизвести свою копию (будучи помещенной в резервуар с необходимыми запасными частями и комплектующими). <br><br>Таким образом, в принципе возможна машинная [[Случайна_ли_эволюция|эволюция]], многократно обыгранная в научно-фантастических романах, где сталкиваются человеческая и машинная цивилизации или их представители. Нейрофизиологи обнаружили, что нейронные сети человеческого мозга во многом состоят из подобных по строению клеток, которые могут находиться в возбужденном или в заторможенном состояниях. Нейронные сообщества - участки коры мозга из нескольких сотен клеток, связанных между собой синаптическими связями, считаются единичными модулями коры. Было показано, что уже простые модельные нейронные сети, состояние ячейки которой зависит от силы воздействия соседей, способны создавать свои точные копии. <br><br>Более того, при циклическом и синхронном изменении порогов срабатывания нейронов (перехода между двумя состояниями) в связанных между собой модулях распространяются волны «обучения», когда модули воспроизводят в себе информацию, содержащуюся в соседнем участке (самовоспроизводят информацию), что проливает свет на процесс запоминания и распознавания образов человеком [18]. Самовоспроизведение и связанный с ним эффект образования однородных областей, состоящих из одинаковых нейронных сетей, естественным образом объясняет дифференциацию и специализацию различных участков мозга как результат спонтанной самоорганизации системы взаимодействующих нейросетей. <br><br>Общий вывод, который следует из приведенных примеров, состоит в том, что такие важнейшие свойства совместно эволюционирующих систем ([[Гравитация_и_Вселенная|Вселенная]], звезды, жизнь на Земле и разум), как сложность, устойчивость, кажущаяся целенаправленность развития, могут быть следствием простых явлений, управляемых совокупностью общих законов. <br><br>Фактически в этом основа формирующейся эволюционно-синергетической парадигмы современного естествознания. В её рамках целью отдельных наук и научных направлений является поиск тех простых правил, которые и порождают изумительное разнообразие структур и форм в окружающем человека мире. <br><br><br><br><br> |
| | | | |
| | ''Концепции современного естествознания. Стародубцев В.А., 2-е изд., доп. — Томск.: Том. политех. ун-т, 2002. — 184 с.'' | | ''Концепции современного естествознания. Стародубцев В.А., 2-е изд., доп. — Томск.: Том. политех. ун-т, 2002. — 184 с.'' |
Текущая версия на 06:31, 9 июля 2012
Гипермаркет знаний>>Естествознание>>Естествознание 11 класс>> Сложность простых систем
7.3. Сложность простых систем
Показателем сложности системы и её логической мощности может служить количество информационно-энергетических каналов связи (взаимодействия) с окружающей средой. В механике связи обычно ограничивают свободу передвижения некоторой части тела или отдельного объекта. Для высокоорганизованных систем, адаптирующихся к окружающей среде, наоборот, увеличение числа жающей среде, наоборот, увеличение числа связей - каналов восприятия информации - повышает свободу «маневра» системы или организма. При высокой сложности на передний план выступает не столько обмен энергией, сколько обмен информацией. Прием информации (при соответствующих затратах энергии) повышает упорядоченность системы, то есть эквивалентен уменьшению её энтропии.
Отмечая это, мы должны иметь в виду, что сложное поведение некоторой системы может быть следствием достаточно простых законов, правил отбора, алгоритмов, на основе которых функционируют (работают, живут) технические системы или живые организмы.
В предыдущем разделе мы привели примеры нелинейных зависимостей, неожиданно приводящих к динамическому хаосу. Здесь же уместно рассмотреть примеры того, как простые правила поведения элементов системы могут приводить к упорядоченным и достаточно сложным процессам кратного воспроизводства начальной конфигурации, направленным движениям и устойчивым структурам. Речь пойдет об эволюции состояний (движении состояний) в системах, где её одинаковые элементы взаимодействуют друг с другом, по крайней мере с ближайшими соседями. Элементами системы являются ячейки или клетки, которые могут находиться в двух состояниях: активном и пассивном, или включенном и выключенном, или живом и мертвом. Ячейки могут составлять правильные плоские или пространственные сети, примерами могут быть шахматная доска, лист тетради в клетку или экран компьютера, разделенный на квадратные или прямоугольные ячейки.
В 1960 г. Э. Фредкин (США) предложил вариант системы, в которой будущее состояние любой и каждой ячейки определяется текущим состоянием четырех ближайших соседей (расположенных к северу, востоку, югу и западу от выбранной). Ячейка, окруженная нечетным числом живых соседей, остается живой. Если число живых соседей четное, то ячейка умирает или остается мертвой. При таких законах жизни и смерти «клеток» любая начально заданная конфигурация колонии воспроизводится четырехкратно после определенного числа смены поколений.
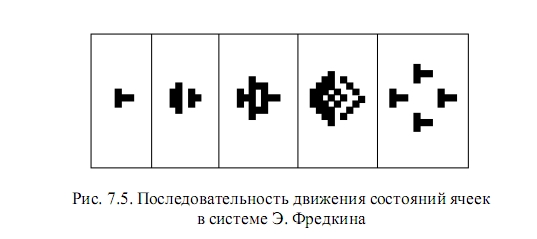
Позже и сами копии учетверятся, и процесс размножения циклически продолжится, пока хватает клеточного поля. Периметр занятой колонией зоны расширяется, а её внутренняя область периодически то заполняется густой «порослью», то снова пустеет.
Вариант Э. Фредкина приводит к размножению копий начального формата и их расхождению, что создает иллюзию экспансии живых клеток.
Если учитывать большее число возможных связей, то поведение системы становится более сложным и менее предсказуемым заранее. В 1970 г. Дж. Конвэй (Великобритания) изобрел игру «Жизнь», в которой учитываются не 4, а 8 соседей каждой клетки (включая соседей второй координационной сферы, соединенных с выбранной клеткой по углам) [19]. Законы жизни и смерти установлены таким образом: живая клетка продолжит свое существование в следующем поколении лишь в тех случаях, когда в её окружении на данном этапе находятся две или три живых соседних ячейки. При меньшем числе живых соседей считается, что клетка умирает от одиночества, а при большем - от тесноты (стресса!). Для неживой клетки возрождение происходит только тогда, когда в её окружении будет ровно 3 живых ячейки.
В «Жизни» Конвэя движение состояний сильно зависит от формы начальной, зародышевой колонии клеток. Одна и две клетки сразу гибнут от одиночества, три клетки образуют стабильные циклические «мигалки», квадрат из четырех ячеек не изменяется. При большем числе исходных ячеек в колонии возникают разнообразные варианты: от быстрого вымирания до расходящихся и сближающихся «островов жизни», узоров или цветов (особенно если последующие поколения отмечаются своим цветом). В процессе движения состояний системы она может распадаться на стабильные циклические конфигурации и на направленно перемещающиеся по полю самовоспроизводящиеся фигуры, иногда довольно сложные.
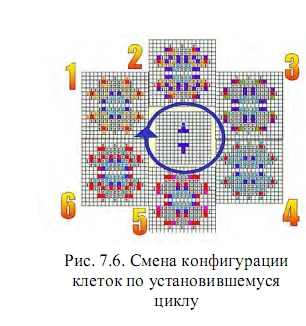
После 30-го шага от начальной конфигурации (в центре), система выходит на цикл, представленный на рисунке. В нем постоянно живы красные и синие клетки. Желтые, зеленые, розовые - появляются циклически.
Практически невозможно описать возможные изменения начальных форм колоний или их эволюцию, лучше воспроизвести «Жизнь» в компьютерной лабораторной работе. Важно отметить, что увеличение числа связей с окружением - в данном случае переход от системы Фредкина к системе Конвэя - приводит к существенному усложнению получающихся в процессе движения состояний форм живых или активных элементов. Исходная простота оборачивается сложностью (геометрической формы активных элементов), устойчивостью (в циклах повторяющегося самовоспроизводства), кажущейся целенаправленностью (в случаях упорядоченного перемещения воспроизводящихся фигур) и принципиальной творческой потенцией (в смысле способности производства новых конфигураций). В ещё большей мере это проявляется в трехмерных компьютерных версиях «Жизни», когда число взаимодействующих соседей заметно возрастает.
Рассмотренные игры являются, конечно, лишь отдаленной аналогией реальным процессам в окружающем мире (скорее, даже аллегорией). Однако такой видный основатель информатики как фон Нейман, всерьез доказал, что если каждая клетка имеет свой клеточный автомат (устройство), способный находиться в 29 состояниях, то при наличии сети из 200 тыс. ячеек информационно-логическая система (или Машина) способна самовоспроизвести свою копию (будучи помещенной в резервуар с необходимыми запасными частями и комплектующими).
Таким образом, в принципе возможна машинная эволюция, многократно обыгранная в научно-фантастических романах, где сталкиваются человеческая и машинная цивилизации или их представители. Нейрофизиологи обнаружили, что нейронные сети человеческого мозга во многом состоят из подобных по строению клеток, которые могут находиться в возбужденном или в заторможенном состояниях. Нейронные сообщества - участки коры мозга из нескольких сотен клеток, связанных между собой синаптическими связями, считаются единичными модулями коры. Было показано, что уже простые модельные нейронные сети, состояние ячейки которой зависит от силы воздействия соседей, способны создавать свои точные копии.
Более того, при циклическом и синхронном изменении порогов срабатывания нейронов (перехода между двумя состояниями) в связанных между собой модулях распространяются волны «обучения», когда модули воспроизводят в себе информацию, содержащуюся в соседнем участке (самовоспроизводят информацию), что проливает свет на процесс запоминания и распознавания образов человеком [18]. Самовоспроизведение и связанный с ним эффект образования однородных областей, состоящих из одинаковых нейронных сетей, естественным образом объясняет дифференциацию и специализацию различных участков мозга как результат спонтанной самоорганизации системы взаимодействующих нейросетей.
Общий вывод, который следует из приведенных примеров, состоит в том, что такие важнейшие свойства совместно эволюционирующих систем (Вселенная, звезды, жизнь на Земле и разум), как сложность, устойчивость, кажущаяся целенаправленность развития, могут быть следствием простых явлений, управляемых совокупностью общих законов.
Фактически в этом основа формирующейся эволюционно-синергетической парадигмы современного естествознания. В её рамках целью отдельных наук и научных направлений является поиск тех простых правил, которые и порождают изумительное разнообразие структур и форм в окружающем человека мире.
Концепции современного естествознания. Стародубцев В.А., 2-е изд., доп. — Томск.: Том. политех. ун-т, 2002. — 184 с.
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|













