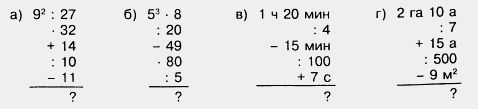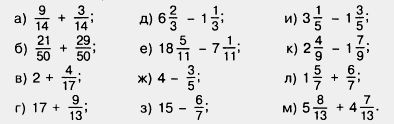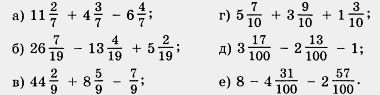|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' Сравнение десятичных дробей ''' | + | '''Сравнение десятичных дробей ''' |
| | | | |
| - | <br>Пусть длина отрезка АВ равна 6 см, то есть 60 мм. Так как 1 см = [[Image:17-06-112.jpg]] дм, то 6 см = [[Image:17-06-113.jpg]] дм. Значит, АВ - 0,6 дм. Так как 1 мм = [[Image:17-06-114.jpg]] дм, то <br>60 мм = [[Image:17-06-115.jpg]] дм. Значит, АВ = 0,60 дм. <br>Таким образом, АВ = 0,6 дм = 0,60 дм. Значит, десятичные дроби 0,6 и 0,60 выражают длину одного и того же отрезка в дециметрах. Эти дроби равны друг другу: 0,6 = 0,60. <br>Если в конце десятичной дроби приписать нуль или отбросить нуль, то получится дробь, равная данной. <br>Например, <br>''' 0,87 = 0,870 = 0,8700; 141 = 141,0 = 141,00 = 141,000; <br> 26,000 = 26,00 = 26,0 = 26; 60,00 = 60,0 = 60; <br> 0,900 = 0,90 = 0,9.''' | + | <br>Пусть длина отрезка АВ равна 6 см, то есть 60 мм. Так как 1 см = [[Image:17-06-112.jpg]] дм, то 6 см = [[Image:17-06-113.jpg]] дм. Значит, АВ - 0,6 дм. Так как 1 мм = [[Image:17-06-114.jpg]] дм, то 60 мм = [[Image:17-06-115.jpg]] дм. Значит, АВ = 0,60 дм. <br>Таким образом, АВ = 0,6 дм = 0,60 дм. Значит, десятичные дроби 0,6 и 0,60 выражают длину одного и того же отрезка в дециметрах. Эти дроби равны друг другу: 0,6 = 0,60. |
| | | | |
| - | Сравним две десятичные дроби 5,345 и 5,36. Уравняем число десятичных знаков, приписав к числу 5,36 справа нуль. Получаем дроби 5,345 и 5,360. <br>Запишем их в виде неправильных дробей:
| + | Если в конце десятичной дроби приписать нуль или отбросить нуль, то получится дробь, равная данной. <br>Например, |
| | | | |
| - | [[Image:17-06-116.jpg]]<br><br>У этих дробей одинаковые знаменатели. Значит, та из них больше, у которой больше числитель. <br>Так как 5345 < 5360, то [[Image:17-06-117.jpg]] а значит, 5,345 < 5,360, то есть 5,345 < 5,36. <br>Чтобы сравнить две десятичные дроби, надо сначала уравнять у них число десятичных знаков, приписав к одной из них справа нули, а потом, отбросив запятую, сравнить получившиеся натуральные числа.
| + | 0,87 = 0,870 = 0,8700; 141 = 141,0 = 141,00 = 141,000; <br>26,000 = 26,00 = 26,0 = 26; 60,00 = 60,0 = 60; <br>0,900 = 0,90 = 0,9. |
| | | | |
| - | Десятичные дроби можно изображать на координатном луче так же, как и обыкновенные дроби. <br>Например, чтобы изобразить на координатном луче десятичную дробь 0,4, сначала представим ее в виде обыкновенной дроби: 0,4 = [[Image:17-06-118.jpg]]• Затем отложим от начала луча четыре десятых единичного отрезка. Получим точку A(0,4) (рис. 141). <br>Равные десятичные дроби изображаются на координатном луче одной и той же точкой.
| + | Сравним две десятичные дроби 5,345 и 5,36. Уравняем число десятичных знаков, приписав к числу 5,36 справа нуль. Получаем дроби 5,345 и 5,360. |
| | | | |
| - | Например, дроби 0,6 и 0,60 изображаются одной точкой В (см. рис. 141). <br>Меньшая десятичная дробь лежит на координатном луче левее большей, и большая — правее меньшей.
| + | Запишем их в виде неправильных дробей: |
| | | | |
| - | [[Image:17-06-119.jpg]]<br><br>Например, 0,4 < 0,6 < 0,8, поэтому точка A(0,4) лежит левее точки B(0,6), а точка С(0,8) лежит правее точки B(0,6) (см. рис. 141). | + | [[Image:17-06-116.jpg|320px|Неправильные дроби]]<br><br>У этих дробей одинаковые знаменатели. Значит, та из них больше, у которой больше числитель. <br>Так как 5345 < 5360, то [[Image:17-06-117.jpg|Сравнение дробей]] а значит, 5,345 < 5,360, то есть 5,345 < 5,36. <br>Чтобы сравнить две десятичные дроби, надо сначала уравнять у них число десятичных знаков, приписав к одной из них справа нули, а потом, отбросив запятую, сравнить получившиеся натуральные числа. |
| | | | |
| - | <br>'''Изменится ли десятичная дробь, если в конце ее приписать нуль? <br>А6 нулей? <br>Сформулируйте правило сравнения десятичных дробей.''' | + | Десятичные дроби можно изображать на координатном луче так же, как и обыкновенные дроби. <br>Например, чтобы изобразить на координатном луче десятичную дробь 0,4, сначала представим ее в виде обыкновенной дроби: 0,4 = [[Image:17-06-118.jpg]]• Затем отложим от начала луча четыре десятых единичного отрезка. Получим точку A(0,4) (рис. 141). |
| | | | |
| - | <br>1172. Напишите десятичную дробь:
| + | Равные десятичные дроби изображаются на координатном луче одной и той же точкой. |
| | | | |
| - | а) с четырьмя знаками после запятой, равную 0,87; <br>б) с пятью знаками после запятой, равную 0,541; <br>в) с тремя знаками после занятой, равную 35; <br>г) с двумя знаками после запятой, равную 8,40000.
| + | Например, дроби 0,6 и 0,60 изображаются одной точкой В (см. рис. 141). |
| | | | |
| - | 1173. Приписав справа нули, уравняйте число знаков после запятой в десятичных дробях:
| + | Меньшая десятичная дробь лежит на координатном луче левее большей, и большая — правее меньшей. |
| | | | |
| - | 1,8; 13,54 и 0,789.
| + | [[Image:17-06-119.jpg|480px|Задание]]<br><br>Например, 0,4 < 0,6 < 0,8, поэтому точка A(0,4) лежит левее точки B(0,6), а точка С(0,8) лежит правее точки B(0,6) (см. рис. 141). |
| | + | |
| | + | ''<br>Изменится ли десятичная дробь, если в конце ее приписать нуль? <br>А6 нулей? <br>Сформулируйте правило сравнения десятичных дробей.'' |
| | + | |
| | + | <br>1172. Напишите десятичную дробь: |
| | + | |
| | + | а) с четырьмя знаками после запятой, равную 0,87; <br>б) с пятью знаками после запятой, равную 0,541; <br>в) с тремя знаками после занятой, равную 35; <br>г) с двумя знаками после запятой, равную 8,40000. |
| | | | |
| - | 1174. Запишите короче дроби:
| + | 1173. Приписав справа нули, уравняйте число знаков после запятой в десятичных дробях:1,8; 13,54 и 0,789. |
| | | | |
| - | 2,5000; 3,02000; 20,010. | + | 1174. Запишите короче дроби:2,5000; 3,02000; 20,010. |
| | | | |
| - | [[Image:17-06-120.jpg]] | + | [[Image:17-06-120.jpg|550px|Правило]] |
| | | | |
| | <br> | | <br> |
| Строка 55: |
Строка 61: |
| | а) А(1,2) или B(1,7); <br>б) С(0,31) или D(0,35); <br>в) E(3,3) или K(3,25)? | | а) А(1,2) или B(1,7); <br>б) С(0,31) или D(0,35); <br>в) E(3,3) или K(3,25)? |
| | | | |
| - | 1179. Какая из точек лежит правее на координатном луче: <br>а) А(2,8) или B(2,4); <br>б) С(0,45) или D(0,49); <br>в) T(7,85) или K(7,9)? | + | 1179. Какая из точек лежит правее на координатном луче: |
| | + | |
| | + | а) А(2,8) или B(2,4); <br>б) С(0,45) или D(0,49); <br>в) T(7,85) или K(7,9)? |
| | | | |
| | 1180. Замените звездочки знаками < или > так, чтобы получилось верное неравенство: | | 1180. Замените звездочки знаками < или > так, чтобы получилось верное неравенство: |
| Строка 85: |
Строка 93: |
| | 1185. Вычислите устно: | | 1185. Вычислите устно: |
| | | | |
| - | [[Image:17-06-121.jpg]]<br><br>1186. Восстановите цепочку вычислений | + | [[Image:17-06-121.jpg|480px|Задание]]<br><br>1186. Восстановите цепочку вычислений |
| | | | |
| - | [[Image:17-06-122.jpg]] | + | [[Image:17-06-122.jpg|480px|Задание]] |
| | | | |
| | <br> | | <br> |
| | | | |
| - | 1187. Можно ли сказать, сколько цифр после запятой в записи десятичной дроби, если ее название заканчивается словом: <br> а) сотых; б) десятитысячных; в) десятых; г) миллионных? | + | 1187. Можно ли сказать, сколько цифр после запятой в записи десятичной дроби, если ее название заканчивается словом: |
| | + | |
| | + | а) сотых; б) десятитысячных; в) десятых; г) миллионных? |
| | | | |
| | 1188. Какую часть килограмма составляют: 1 г; 10 г; 100 г; 300 г? | | 1188. Какую часть килограмма составляют: 1 г; 10 г; 100 г; 300 г? |
| Строка 97: |
Строка 107: |
| | 1189. Найдите число, если [[Image:17-06-123.jpg]] его равна: 20; 15; 3; 1. | | 1189. Найдите число, если [[Image:17-06-123.jpg]] его равна: 20; 15; 3; 1. |
| | | | |
| - | 1190. Используя рисунок 142, попробуйте догадаться, какое число стоит вместо звездочки: [[Image:17-06-124.jpg]]<br><br>[[Image:17-06-125.jpg]] | + | 1190. Используя рисунок 142, попробуйте догадаться, какое число стоит вместо звездочки: |
| | + | |
| | + | [[Image:17-06-124.jpg|320px|Задание]]<br><br>[[Image:17-06-125.jpg|480px|Задание]] |
| | | | |
| | <br>1191. Все шесть граней куба — квадраты. Подумайте, какие из фигур, изображенных на рисунке 143, являются разверткой поверхности куба. | | <br>1191. Все шесть граней куба — квадраты. Подумайте, какие из фигур, изображенных на рисунке 143, являются разверткой поверхности куба. |
| | | | |
| - | [[Image:17-06-126.jpg]]<br><br>1192. Выразите в тоннах и килограммах: | + | [[Image:17-06-126.jpg|550px|Задание]]<br><br>1192. Выразите в тоннах и килограммах: |
| | | | |
| | а) 3,236 т; в) 0,006 т; д) 8,009 т; <br>б) 11,800 т; г) 7,001 т; е) 10,001 т. | | а) 3,236 т; в) 0,006 т; д) 8,009 т; <br>б) 11,800 т; г) 7,001 т; е) 10,001 т. |
| Строка 109: |
Строка 121: |
| | а) в миллионах: 8 984 000; 91,78 млрд; <br>б) в тысячах: 1306; 8,065 млн; 17,8 млрд. <br> | | а) в миллионах: 8 984 000; 91,78 млрд; <br>б) в тысячах: 1306; 8,065 млн; 17,8 млрд. <br> |
| | | | |
| - | [[Image:17-06-127.jpg]] | + | [[Image:17-06-127.jpg|480px|Весы]] |
| | | | |
| | <br>1194. Какую массу показывают каждые весы (рис. 144)? Запишите результат в килограммах. | | <br>1194. Какую массу показывают каждые весы (рис. 144)? Запишите результат в килограммах. |
| Строка 119: |
Строка 131: |
| | 1196. Решите задачу: | | 1196. Решите задачу: |
| | | | |
| - | а) Теплоход идет вниз по реке. Какова скорость движения теплохода, если скорость течения реки 4 км/ч, а собственная скорость теплохода (скорость в <br>стоячей воде) равна 21 км/ч? <br>б) Моторная лодка идет вверх по реке. Какова скорость движения лодки, если скорость течения 3 км/ч, а собственная скорость лодки 14 км/ч? | + | а) Теплоход идет вниз по реке. Какова скорость движения теплохода, если скорость течения реки 4 км/ч, а собственная скорость теплохода (скорость в стоячей воде) равна 21 км/ч? |
| | + | |
| | + | б) Моторная лодка идет вверх по реке. Какова скорость движения лодки, если скорость течения 3 км/ч, а собственная скорость лодки 14 км/ч? |
| | | | |
| | 1197. Разложите по разрядам числа: | | 1197. Разложите по разрядам числа: |
| Строка 127: |
Строка 141: |
| | 1198. Выполните действие: | | 1198. Выполните действие: |
| | | | |
| - | [[Image:17-06-128.jpg]]<br><br><br>1199. Решите задачу: | + | [[Image:17-06-128.jpg|480px|Задание]]<br><br>1199. Решите задачу: |
| | + | |
| | + | 1) Со станции вышел товарный поезд со скоростью 50 км/ч. Через 3 ч с той же станции вслед за ним вышел электропоезд со скоростью 80 км/ч. Через сколько часов после своего выхода электропоезд догонит товарный поезд? |
| | | | |
| - | 1) Со станции вышел товарный поезд со скоростью 50 км/ч. Через 3 ч с той же станции вслед за ним вышел электропоезд со скоростью 80 км/ч. Через <br>сколько часов после своего выхода электропоезд догонит товарный поезд? <br>2) Самолет вылетел с аэродрома со скоростью 500 км/ч. Через 2 ч с этого же аэродрома в том же направлении вылетел другой самолет со скоростью <br>700 км/ч. Через сколько часов после вылета второй самолет догонит первый?
| + | 2) Самолет вылетел с аэродрома со скоростью 500 км/ч. Через 2 ч с этого же аэродрома в том же направлении вылетел другой самолет со скоростью 700 км/ч. Через сколько часов после вылета второй самолет догонит первый? |
| | | | |
| | 1200. Сравните числа: | | 1200. Сравните числа: |
| Строка 145: |
Строка 161: |
| | 1205. Выполните действия: | | 1205. Выполните действия: |
| | | | |
| - | [[Image:17-06-129.jpg]]<br><br>1206. Два поезда вышли в разное время навстречу друг другу из двух городов, расстояние между которыми 782 км. Скорость первого поезда 52 км/ч, а второго 61 км/ч. Пройдя 416 км, первый поезд встретился со вторым. На сколько один из поездов вышел раньше другого? | + | [[Image:17-06-129.jpg|480px|Задание]]<br><br>1206. Два поезда вышли в разное время навстречу друг другу из двух городов, расстояние между которыми 782 км. Скорость первого поезда 52 км/ч, а второго 61 км/ч. Пройдя 416 км, первый поезд встретился со вторым. На сколько один из поездов вышел раньше другого? |
| | | | |
| - | 1207. С одной и той же станции в одно и то же время вышли в противоположных направлениях два поезда. Скорость одного поезда 50 км/ч, а скорость другого 85 км/ч. Через какое время расстояние между ними будет равно 540 км? | + | 1207. С одной и той же станции в одно и то же время вышли в противоположных направлениях два поезда. |
| | + | |
| | + | Скорость одного поезда 50 км/ч, а скорость другого 85 км/ч. Через какое время расстояние между ними будет равно 540 км? |
| | | | |
| | 1208. Чтобы добраться из города до села, я проехал 5 ч на поезде, 2 ч на автобусе и 3 ч прошел пешком. Скорость автобуса была 35 км/ч, скорость поезда вдвое больше скорости автобуса, а пешком я шел со скоростью, на 65 км/ч меньшей, чем скорость поезда. Какой путь я проделал от города до села? | | 1208. Чтобы добраться из города до села, я проехал 5 ч на поезде, 2 ч на автобусе и 3 ч прошел пешком. Скорость автобуса была 35 км/ч, скорость поезда вдвое больше скорости автобуса, а пешком я шел со скоростью, на 65 км/ч меньшей, чем скорость поезда. Какой путь я проделал от города до села? |
| Строка 155: |
Строка 173: |
| | 1210. Решите уравнение: | | 1210. Решите уравнение: |
| | | | |
| - | а) 14x - (8х + Зх) = 1512; | + | а) 14x - (8х + Зх) = 1512; |
| | | | |
| | б) 11у - (bу - Зу) = 8136. <br> | | б) 11у - (bу - Зу) = 8136. <br> |
| | | | |
| | + | <br> ''Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, [http://xvatit.com/vuzi/ '''Математика'''] 5 класс, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| | | | |
| - | <br> ''Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| - | <sub>Полный перечень тем по классам, календарный план согласно школьной программе по математике [[Гипермаркет знаний - первый в мире!|онлайн]], видеоматериал по математике для 5 класса [[Математика|скачать]]</sub> | + | <sub>Полный перечень тем по классам, календарный план согласно школьной программе по математике [[Гипермаркет знаний - первый в мире!|онлайн]], видеоматериал по математике для 5 класса [[Математика|скачать]]</sub><br> |
| - | | + | |
| - | <br> | + | |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Версия 18:24, 5 октября 2012
Гипермаркет знаний>>Математика>>Математика 5 класс>>Математика:Сравнение десятичных дробей
Сравнение десятичных дробей
Пусть длина отрезка АВ равна 6 см, то есть 60 мм. Так как 1 см = 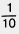 дм, то 6 см = дм, то 6 см = 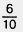 дм. Значит, АВ - 0,6 дм. Так как 1 мм = дм. Значит, АВ - 0,6 дм. Так как 1 мм = 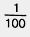 дм, то 60 мм = дм, то 60 мм = 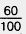 дм. Значит, АВ = 0,60 дм. дм. Значит, АВ = 0,60 дм.
Таким образом, АВ = 0,6 дм = 0,60 дм. Значит, десятичные дроби 0,6 и 0,60 выражают длину одного и того же отрезка в дециметрах. Эти дроби равны друг другу: 0,6 = 0,60.
Если в конце десятичной дроби приписать нуль или отбросить нуль, то получится дробь, равная данной.
Например,
0,87 = 0,870 = 0,8700; 141 = 141,0 = 141,00 = 141,000;
26,000 = 26,00 = 26,0 = 26; 60,00 = 60,0 = 60;
0,900 = 0,90 = 0,9.
Сравним две десятичные дроби 5,345 и 5,36. Уравняем число десятичных знаков, приписав к числу 5,36 справа нуль. Получаем дроби 5,345 и 5,360.
Запишем их в виде неправильных дробей:

У этих дробей одинаковые знаменатели. Значит, та из них больше, у которой больше числитель.
Так как 5345 < 5360, то  а значит, 5,345 < 5,360, то есть 5,345 < 5,36. а значит, 5,345 < 5,360, то есть 5,345 < 5,36.
Чтобы сравнить две десятичные дроби, надо сначала уравнять у них число десятичных знаков, приписав к одной из них справа нули, а потом, отбросив запятую, сравнить получившиеся натуральные числа.
Десятичные дроби можно изображать на координатном луче так же, как и обыкновенные дроби.
Например, чтобы изобразить на координатном луче десятичную дробь 0,4, сначала представим ее в виде обыкновенной дроби: 0,4 = 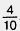 • Затем отложим от начала луча четыре десятых единичного отрезка. Получим точку A(0,4) (рис. 141). • Затем отложим от начала луча четыре десятых единичного отрезка. Получим точку A(0,4) (рис. 141).
Равные десятичные дроби изображаются на координатном луче одной и той же точкой.
Например, дроби 0,6 и 0,60 изображаются одной точкой В (см. рис. 141).
Меньшая десятичная дробь лежит на координатном луче левее большей, и большая — правее меньшей.

Например, 0,4 < 0,6 < 0,8, поэтому точка A(0,4) лежит левее точки B(0,6), а точка С(0,8) лежит правее точки B(0,6) (см. рис. 141).
Изменится ли десятичная дробь, если в конце ее приписать нуль?
А6 нулей?
Сформулируйте правило сравнения десятичных дробей.
1172. Напишите десятичную дробь:
а) с четырьмя знаками после запятой, равную 0,87;
б) с пятью знаками после запятой, равную 0,541;
в) с тремя знаками после занятой, равную 35;
г) с двумя знаками после запятой, равную 8,40000.
1173. Приписав справа нули, уравняйте число знаков после запятой в десятичных дробях:1,8; 13,54 и 0,789.
1174. Запишите короче дроби:2,5000; 3,02000; 20,010.

1175. Сравните числа:
85,09 и 67,99; 55,7 и 55,7000; 0,5 и 0,724; 0,908 и 0,918; 7,6431 и 7,6429; 0,0025 и 0,00247.
1176. Расставьте в порядке возрастания числа:
3,456; 3,465; 8,149; 8,079; 0,453.
А числа
0,0082; 0,037; 0,0044; 0,08; 0,0091
расставьте в порядке убывания.
1177. Примите за единичный отрезок длину десяти клеток тетради и отметьте на координатном луче точки А(0,1), B(0,5), С(0,9), D(l,2), E(1,7).
1178. Какая из точек лежит левее на координатном луче:
а) А(1,2) или B(1,7);
б) С(0,31) или D(0,35);
в) E(3,3) или K(3,25)?
1179. Какая из точек лежит правее на координатном луче:
а) А(2,8) или B(2,4);
б) С(0,45) или D(0,49);
в) T(7,85) или K(7,9)?
1180. Замените звездочки знаками < или > так, чтобы получилось верное неравенство:
21 * 18,75; 8,006 * 9,0001; 7,2 * 7,2005; 4,009 * 3,999.
1181. Какие цифры можно поставить вместо звездочки, чтобы получилось верное неравенство:
а) 2,*1 > 2,01;
б) 1,34 < 1,3*?
1182. Между какими соседними натуральными числами находится дробь:
а) 2,7; б)12,21;
в) 3,343; г) 9,111?
1183. Найдите какое-нибудь значение х, при котором верно неравенство:
а) 1,41 < х < 4,75; г) 2,99 < х < 3;
б) 0,1 < х < 0,2; д) 7 < х < 7,01;
в) 2,7 < х < 2,8; е) 0,12 < х < 0,13.
1184. Сравните величины:
а) 98,52 м и 65,39 м; д) 0,605 т и 691,3 кг;
б) 149,63 кг и 150,08 кг; е) 4,572 км и 4671,3 м;
в) 3,55°С и 3,61°С; ж) 3,835 га и 383,7 а;
г) 6,781 ч и 6,718 ч; з) 7,521 л и 7538 см3.
Можно ли сравнить 3,5 кг и 8,12 м? Приведите несколько примеров величин, которые нельзя сравнивать.
1185. Вычислите устно:
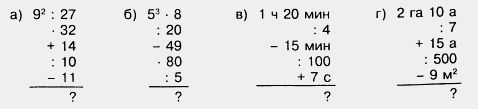
1186. Восстановите цепочку вычислений
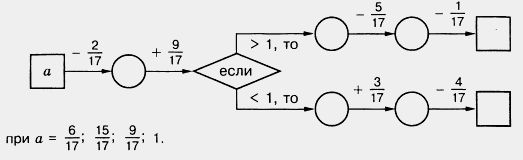
1187. Можно ли сказать, сколько цифр после запятой в записи десятичной дроби, если ее название заканчивается словом:
а) сотых; б) десятитысячных; в) десятых; г) миллионных?
1188. Какую часть килограмма составляют: 1 г; 10 г; 100 г; 300 г?
1189. Найдите число, если 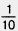 его равна: 20; 15; 3; 1. его равна: 20; 15; 3; 1.
1190. Используя рисунок 142, попробуйте догадаться, какое число стоит вместо звездочки:
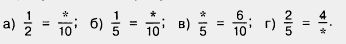

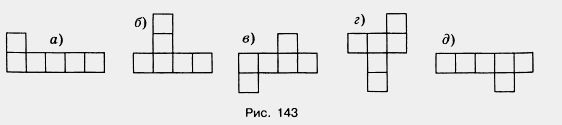
1191. Все шесть граней куба — квадраты. Подумайте, какие из фигур, изображенных на рисунке 143, являются разверткой поверхности куба.
1192. Выразите в тоннах и килограммах:
а) 3,236 т; в) 0,006 т; д) 8,009 т;
б) 11,800 т; г) 7,001 т; е) 10,001 т.
1193. Выразите:
а) в миллионах: 8 984 000; 91,78 млрд;
б) в тысячах: 1306; 8,065 млн; 17,8 млрд.
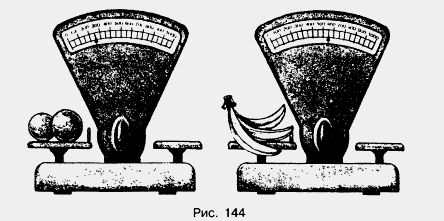
1194. Какую массу показывают каждые весы (рис. 144)? Запишите результат в килограммах.
1195. Запишите в виде десятичных дробей частные:
7206 : 100; 61 : 1000; 7 : 100; 1849 : 1000.
1196. Решите задачу:
а) Теплоход идет вниз по реке. Какова скорость движения теплохода, если скорость течения реки 4 км/ч, а собственная скорость теплохода (скорость в стоячей воде) равна 21 км/ч?
б) Моторная лодка идет вверх по реке. Какова скорость движения лодки, если скорость течения 3 км/ч, а собственная скорость лодки 14 км/ч?
1197. Разложите по разрядам числа:
5089; 6 781 802; 8000; 98 000 560.
1198. Выполните действие:
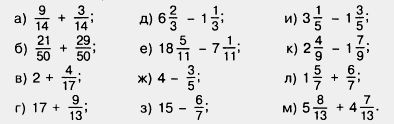
1199. Решите задачу:
1) Со станции вышел товарный поезд со скоростью 50 км/ч. Через 3 ч с той же станции вслед за ним вышел электропоезд со скоростью 80 км/ч. Через сколько часов после своего выхода электропоезд догонит товарный поезд?
2) Самолет вылетел с аэродрома со скоростью 500 км/ч. Через 2 ч с этого же аэродрома в том же направлении вылетел другой самолет со скоростью 700 км/ч. Через сколько часов после вылета второй самолет догонит первый?
1200. Сравните числа:
а) 3,573 и 3,581; в) 7,299 и 7,3; д) 3,29 и 3,3;
б) 8,605 и 8,59; г) 6,504 и 6,505; е) 4,85 и 0,1.
1201. Напишите все цифры, которые можно поставить вместо звездочки, чтобы получилось верное неравенство:
а) 0,*3 > 0,13; в) 5,64 > 5,*8; д) 12,*4 > 12,53;
б) 0,1* < 0,18; г) 3,51 < 3,*1; е) 0,001 < 0,0*1.
1202. Напишите число, меньшее 0,000001.
1203. Примите за единичный отрезок длину десяти клеток тетради и отметьте на координатном луче точки: А(0,7), В(1,2), С(1,8).
1204. Разложите по разрядам 49 008 и 67 813 742.
1205. Выполните действия:
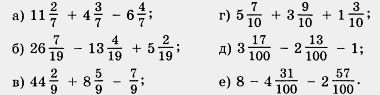
1206. Два поезда вышли в разное время навстречу друг другу из двух городов, расстояние между которыми 782 км. Скорость первого поезда 52 км/ч, а второго 61 км/ч. Пройдя 416 км, первый поезд встретился со вторым. На сколько один из поездов вышел раньше другого?
1207. С одной и той же станции в одно и то же время вышли в противоположных направлениях два поезда.
Скорость одного поезда 50 км/ч, а скорость другого 85 км/ч. Через какое время расстояние между ними будет равно 540 км?
1208. Чтобы добраться из города до села, я проехал 5 ч на поезде, 2 ч на автобусе и 3 ч прошел пешком. Скорость автобуса была 35 км/ч, скорость поезда вдвое больше скорости автобуса, а пешком я шел со скоростью, на 65 км/ч меньшей, чем скорость поезда. Какой путь я проделал от города до села?
1209. Поле в 1260 га засеяли озимой пшеницей вместо яровой и собрали по 28 ц зерна с гектара. Урожайность яровой пшеницы была 18 ц с гектара. Какую прибавку зерна получили со всей площади?
1210. Решите уравнение:
а) 14x - (8х + Зх) = 1512;
б) 11у - (bу - Зу) = 8136.
Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Полный перечень тем по классам, календарный план согласно школьной программе по математике онлайн, видеоматериал по математике для 5 класса скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|