|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | '''Среднее арифметическое '''<br>
| + | '''Среднее арифметическое '''<br> |
| | | | |
| - | <br>'''Задача 1'''. Миша, Коля и Петя были в походе. Подойдя к лесу, они решили сделать привал. У Миши было 2 пирожка, у Пети — 4 и у Коли — 6. Все пирожки мальчики разделили поровну и съели. Сколько пирожков съел каждый? <br> | + | <br>'''Задача 1'''. Миша, Коля и Петя были в походе. Подойдя к лесу, они решили сделать привал. У Миши было 2 пирожка, у Пети — 4 и у Коли — 6. Все пирожки мальчики разделили поровну и съели. Сколько пирожков съел каждый? <br> |
| | | | |
| - | Решение. Всего у мальчиков было 2 + 4 + 6, то есть 12 пирожков. Каждому досталось по 12 : 3, то есть по 4 пирожка. '''Средним арифметическим''' нескольких чисел называют частное от деления суммы этих чисел на число слагаемых. <br> | + | Решение. Всего у мальчиков было 2 + 4 + 6, то есть 12 пирожков. Каждому досталось по 12 : 3, то есть по 4 пирожка. '''Средним арифметическим''' нескольких чисел называют частное от деления суммы этих чисел на число слагаемых. <br> |
| | | | |
| - | [[Image:17-06-202.jpg]]<br> | + | [[Image:17-06-202.jpg|550px|Среднее арифметическое ]]<br> |
| | | | |
| - | '''Задача 2.''' Человек шел 2 ч со скоростью 4,6 км/ч и 3 ч со скоростью 5,1 км/ч. С какой постоянной скоростью он должен был идти, чтобы пройти то же расстояние за то же время? <br>Решение. Найдем все расстояние, которое прошел пешеход: <br> | + | '''Задача 2.''' Человек шел 2 ч со скоростью 4,6 км/ч и 3 ч со скоростью 5,1 км/ч. С какой постоянной скоростью он должен был идти, чтобы пройти то же расстояние за то же время? |
| | | | |
| - | '''4,6 • 2 + 5,1 • 3 = 9,2 + 15,3 = 24,5 (км). '''<br>
| + | Решение. Найдем все расстояние, которое прошел пешеход: <br> |
| | | | |
| - | Разделим полученный результат на время, затраченное на этот путь: <br>24,5 : 5 = 4,9. Получим ответ: пешеход должен идти с постоянной скоростью 4,9 км/ч. Такую скорость называют '''средней скоростью движения.''' <br>
| + | 4,6 • 2 + 5,1 • 3 = 9,2 + 15,3 = 24,5 (км). <br> |
| | | | |
| - | [[Image:17-06-203.jpg]]<br>Этот же ответ можно получить, если найти среднее арифметическое скоростей за каждый час движения: (4,6 + 4,6 + 5,1 + 5,1 + 5,1) : 5 = 4,9. <br>Подобным образом находят среднюю урожайность, среднюю производительность и т. д.<br>
| + | Разделим полученный результат на время, затраченное на этот путь: |
| | | | |
| - | <br>'''Какое число называют средним арифметическим нескольких чисел? <br>Как найти среднее арифметическое нескольких чисел? <br>Как найти среднюю скорость движения? '''<br>
| + | 24,5 : 5 = 4,9. Получим ответ: пешеход должен идти с постоянной скоростью 4,9 км/ч. Такую скорость называют средней скоростью движения. <br> |
| | | | |
| - | <br>1496. Найдите среднее арифметическое чисел 2 и 10. Изобразите на координатном луче число 2, число 10 и их среднее арифметическое. Сделайте вывод. <br> | + | [[Image:17-06-203.jpg|550px|Среднее арифметическое ]]<br>Этот же ответ можно получить, если найти среднее арифметическое скоростей за каждый час движения: (4,6 + 4,6 + 5,1 + 5,1 + 5,1) : 5 = 4,9. |
| | | | |
| - | 1497. Найдите среднее арифметическое чисел: <br>
| + | Подобным образом находят среднюю урожайность, среднюю производительность и т. д. |
| | | | |
| - | а) 70,6 и 71,3; <br>б) 0,1; 0,2 и 0,3; <br>в) 1,11; 1,12; 1,19 и 1,48; <br>г) 7,381; 5,004; 6,118; 8,019; 7,815 и 5,863. <br>
| |
| | | | |
| - | 1498. На рисунке 153 АВ = ВС, где А(8,9) и 5(9,5). Найдите координатуточки С. Чему равно среднее арифметическое координат точек А и С? <br><br>[[Image:17-06-204.jpg]]<br>
| |
| | | | |
| - | 1499. Четыре поля имеют площадь по 200 га каждое. На первом поле собрали 7220 ц пшеницы, на втором — 7560 ц пшеницы, на третьем — 7090 ц пшеницы и на четвертом — 7130 ц пшеницы. Определите урожайность пшеницы на каждом поле и найдите среднюю урожайность. <br>
| + | ''Какое число называют средним арифметическим нескольких чисел? <br>Как найти среднее арифметическое нескольких чисел? <br>Как найти среднюю скорость движения? ''<br> |
| | | | |
| - | 1500. С поля площадью 87 га сняли урожай 10 450 ц картофеля, а с поля площадью 113 га собрали 14 980 ц картофеля. Найдите среднюю урожайность картофеля на этих полях. <br>
| + | <br>1496. Найдите среднее арифметическое чисел 2 и 10. Изобразите на координатном луче число 2, число 10 и их среднее арифметическое. Сделайте вывод. <br> |
| | | | |
| - | 1501. Найдите среднее арифметическое чисел 84,32; 84,47; 84,56 и 84,68 и округлите его до десятых. <br>
| + | 1497. Найдите среднее арифметическое чисел: <br> |
| | | | |
| - | 1502. Участника соревнований пр фщур^шу катанию на коньках получила оценки 5,3; 4,8; 5,4; 5,0; 5,3; 5,4; 5,3; 5,2; 5,1. Найдите среднюю оценку этой участницы. <br>
| + | а) 70,6 и 71,3; <br>б) 0,1; 0,2 и 0,3; <br>в) 1,11; 1,12; 1,19 и 1,48; <br>г) 7,381; 5,004; 6,118; 8,019; 7,815 и 5,863. <br> |
| | | | |
| - | 1503. Автомобиль двигался 3,2 ч по шоссе со скоростью 90 км/ч, затем 1,5 ч по грунтовой дороге со скоростью 45 км/ч, наконец, 0,3 ч по проселочной дороге со скоростью 30 км/ч. Найдите среднюю скорость движения автомобиля на всем пути. <br>
| + | 1498. На рисунке 153 АВ = ВС, где А(8,9) и 5(9,5). Найдите координатуточки С. Чему равно среднее арифметическое координат точек А и С? <br><br>[[Image:17-06-204.jpg|480px|Задание]]<br> |
| | | | |
| - | 1504. Поезд шел 4 ч со скоростью 70 км/ч и 3 ч со скоростью 84 км/ч. Найдите среднюю скорость поезда на пройденном за это время пути. <br>
| + | 1499. Четыре поля имеют площадь по 200 га каждое. На первом поле собрали 7220 ц пшеницы, на втором — 7560 ц пшеницы, на третьем — 7090 ц пшеницы и на четвертом — 7130 ц пшеницы. Определите урожайность пшеницы на каждом поле и найдите среднюю урожайность. <br> |
| | | | |
| - | 1505. Среднее арифметическое двух чисел равно 3,1. Одно число равно 3,8- Найдите второе число. <br>
| + | 1500. С поля площадью 87 га сняли урожай 10 450 ц картофеля, а с поля площадью 113 га собрали 14 980 ц картофеля. Найдите среднюю урожайность картофеля на этих полях. <br> |
| | | | |
| - | [[Image:17-06-205.jpg]]<br>
| + | 1501. Найдите среднее арифметическое чисел 84,32; 84,47; 84,56 и 84,68 и округлите его до десятых. <br> |
| | | | |
| - | 1506. Среднее арифметическое шести чисел равно 3,5, а среднее арифметическое четырех других чисел — 2,25. Найдите среднее арифметическое этих десяти чисел. <br>
| + | 1502. Участника соревнований пр фщур^шу катанию на коньках получила оценки 5,3; 4,8; 5,4; 5,0; 5,3; 5,4; 5,3; 5,2; 5,1. Найдите среднюю оценку этой участницы. <br> |
| | | | |
| - | 1507. На первом участке пути поезд шел 2 ч со скоростью 60 км/ч, а на втором он шел 3 ч. С какой скоростью шел поезд на втором участке, если его средняя скорость на двух участках была равна 51 км/ч? <br>
| + | 1503. Автомобиль двигался 3,2 ч по шоссе со скоростью 90 км/ч, затем 1,5 ч по грунтовой дороге со скоростью 45 км/ч, наконец, 0,3 ч по проселочной дороге со скоростью 30 км/ч. Найдите среднюю скорость движения автомобиля на всем пути. <br> |
| | | | |
| - | 1508. Скорость катера по течению 18,6 км/ч, а против течения 14,2 км/ч. Найдите собственную скорость катера и скорость течения. <br>
| + | 1504. Поезд шел 4 ч со скоростью 70 км/ч и 3 ч со скоростью 84 км/ч. Найдите среднюю скорость поезда на пройденном за это время пути. <br> |
| | | | |
| - | 1509. Одно число больше другого в 1,5 раза, среднее арифметическое этих двух чисел равно 30. Найдите эти числа. <br>
| + | 1505. Среднее арифметическое двух чисел равно 3,1. Одно число равно 3,8- Найдите второе число. <br> |
| | | | |
| - | 1510. Вычислите устно: <br>
| + | [[Image:17-06-205.jpg|550px|Среднее арифметическое]]<br> |
| | | | |
| - | а) 0,14 + 0,06; <br> 2 - 0,7; <br> 100 • 0,012; <br> 0,42 : 7; <br>
| + | 1506. Среднее арифметическое шести чисел равно 3,5, а среднее арифметическое четырех других чисел — 2,25. Найдите среднее арифметическое этих десяти чисел. <br> |
| | | | |
| - | б) 3,18 - 1,08<br>
| + | 1507. На первом участке пути поезд шел 2 ч со скоростью 60 км/ч, а на втором он шел 3 ч. С какой скоростью шел поезд на втором участке, если его средняя скорость на двух участках была равна 51 км/ч? <br> |
| | | | |
| - | 2,06 + 1,04<br>
| + | 1508. Скорость катера по течению 18,6 км/ч, а против течения 14,2 км/ч. Найдите собственную скорость катера и скорость течения. <br> |
| | | | |
| - | 5,4 • 0,1<br>
| + | 1509. Одно число больше другого в 1,5 раза, среднее арифметическое этих двух чисел равно 30. Найдите эти числа. <br> |
| | | | |
| - | 4,08 : 4<br>
| + | 1510. Вычислите устно: <br> |
| | | | |
| - | в) 5,7 + 0,13<br>
| + | а) 0,14 + 0,06; <br> 2 - 0,7; <br> 100 • 0,012; <br> 0,42 : 7; <br> |
| | | | |
| - | 2,85 - 1,5<br>
| + | б) 3,18 - 1,08<br> |
| | | | |
| - | 0,8 • 0,5 | + | 2,06 + 1,04<br> |
| | | | |
| - | 0,5 6 2<br> | + | 5,4 • 0,1<br> |
| | | | |
| - | г) 0,4<sup>2</sup><br>
| + | 4,08 : 4<br> |
| | | | |
| - | 0,3<sup>2</sup><br>
| + | в) 5,7 + 0,13<br> |
| | | | |
| - | 0,05<sup>2</sup><br> | + | 2,85 - 1,5<br> |
| | | | |
| - | 0,01<sup>3</sup><br> | + | 0,8 • 0,5 |
| | | | |
| - | 1511. Выполните деление <br>а) 40 : 0,4; <br>б) 0,8 : 0,2; <br>в) 20 : 0,5; <br>г) 100 : 0,1. <br>д) 1000 : 0,01<br>е) 6 : 0,3; <br>ж) 0,18 : 0,6<br>
| + | 0,5 6 2<br> |
| | | | |
| - | з) 0,1 : 0,01<br>и) 1 : 0,5<br><br>1512. В летний лагерь детей отправляли на 6 одинаковых автобусах. В автобусах оказалось 29, 41, 28, 22, 27 и 33 человека. Можно ли было отъезжающих разместить в автобусах поровну? <br>
| + | г) 0,4<sup>2</sup><br> |
| | | | |
| - | 1513. Вы знаете, что <br>
| + | 0,3<sup>2</sup><br> |
| | | | |
| - | [[Image:17-06-206.jpg]]<br>
| + | 0,05<sup>2</sup><br> |
| | | | |
| - | Поэтому умножить число на 0,5 означает найти половину числа, умножить на 0,125 означает найти восьмую часть числа и т. д. <br>Подумайте, как проще найти значение выражения: <br>
| + | 0,01<sup>3</sup><br> |
| | | | |
| - | а) 400-0,1; в) 84 • 0,25; д) 68 • 0,5. <br>б) 20 • 0,2; г) 16 • 0,125; <br>
| + | 1511. Выполните деление |
| | | | |
| - | Запомните эту таблицу. <br>
| + | а) 40 : 0,4; <br>б) 0,8 : 0,2; <br>в) 20 : 0,5; <br>г) 100 : 0,1. <br>д) 1000 : 0,01<br>е) 6 : 0,3; <br>ж) 0,18 : 0,6<br> |
| | | | |
| - | 1514. Может ли произведение двух чисел оказаться меньше одного из множителей? Меньше обоих множителей? Может ли частное оказаться больше делимого? Приведите примеры. <br>
| + | з) 0,1 : 0,01<br>и) 1 : 0,5<br><br>1512. В летний лагерь детей отправляли на 6 одинаковых автобусах. В автобусах оказалось 29, 41, 28, 22, 27 и 33 человека. Можно ли было отъезжающих разместить в автобусах поровну? <br> |
| | | | |
| - | 1515. Мальчик решил определить длину моста через реку. Он заметил, что расстояние между двумя столбиками, на которых крепятся перила, равнодвум шагам, а столбиков всего 30. Какова длина моста, если один шаг мальчика 0,4 м? <br>
| + | 1513. Вы знаете, что <br> |
| | | | |
| - | 1516. Выполните деление: <br>
| + | [[Image:17-06-206.jpg|480px|Задание]]<br> |
| | | | |
| - | а) 0,432 : 0,24; <br>б) 0,8625 : 0,375; <br>
| + | Поэтому умножить число на 0,5 означает найти половину числа, умножить на 0,125 означает найти восьмую часть числа и т. д. <br>Подумайте, как проще найти значение выражения: <br> |
| | | | |
| - | в) 1,872 : 2,34;<br>
| + | а) 400-0,1; в) 84 • 0,25; д) 68 • 0,5. <br>б) 20 • 0,2; г) 16 • 0,125; <br> |
| | | | |
| - | г) 0,481 : 0,037;<br>д) 41,48 : 34; <br>е) 127,2 : 159. <br>
| + | Запомните эту таблицу. <br> |
| | | | |
| - | 1517. Решите уравнение: <br>
| + | 1514. Может ли произведение двух чисел оказаться меньше одного из множителей? Меньше обоих множителей? Может ли частное оказаться больше делимого? Приведите примеры. <br> |
| | | | |
| - | а) 3,5x - 2,3x + 3,8 = 4,28; в) (8,3 - k) • 4,7 = 5,64; <br>б) 4,7y - (2,5у + 12,4) = 1,9; г) (9,2 - m) • 3,2 = 16. <br>
| + | 1515. Мальчик решил определить длину моста через реку. Он заметил, что расстояние между двумя столбиками, на которых крепятся перила, равнодвум шагам, а столбиков всего 30. Какова длина моста, если один шаг мальчика 0,4 м? <br> |
| | | | |
| - | 1518. Школьная географическая площадка занимает 36 м<sup>2</sup>. Это составляет 0,1 всего пришкольного участка. Найдите площадь пришкольного участка. <br>
| + | 1516. Выполните деление: <br> |
| | | | |
| - | 1519. В 12 ч скорый поезд догнал пассажирский, а в 18 ч был уже впереди его на 120 км. Какое расстояние между поездами было в 10 ч, если скорость - <br>пассажирского поезда 70 км/ч? Какое данное в условии задачи лишнее? <br>
| + | а) 0,432 : 0,24; <br>б) 0,8625 : 0,375; <br> |
| | | | |
| - | 1520. Длина стороны основания пирамиды Хеопса 230 м. Туристы, осматривая пирамиду, идут со скоростью 0,32 м/с. Успеют ли туристы за час обойти ? <br>вокруг пирамиды? <br>
| + | в) 1,872 : 2,34;<br> |
| | | | |
| - | 1521. Заполните таблицу: <br>
| + | г) 0,481 : 0,037;<br>д) 41,48 : 34; <br>е) 127,2 : 159. <br> |
| | | | |
| - | [[Image:17-06-207.jpg]]<br>
| + | 1517. Решите уравнение: <br> |
| | | | |
| - | 1522. Вычислите: <br>
| + | а) 3,5x - 2,3x + 3,8 = 4,28; в) (8,3 - k) • 4,7 = 5,64; <br>б) 4,7y - (2,5у + 12,4) = 1,9; г) (9,2 - m) • 3,2 = 16. <br> |
| | | | |
| - | 1) (7 -5,38) • 2,5<br>
| + | 1518. Школьная географическая площадка занимает 36 м<sup>2</sup>. Это составляет 0,1 всего пришкольного участка. Найдите площадь пришкольного участка. <br> |
| | | | |
| - | 2) (8 - 6,46) •1,5
| + | 1519. В 12 ч скорый поезд догнал пассажирский, а в 18 ч был уже впереди его на 120 км. Какое расстояние между поездами было в 10 ч, если скорость - пассажирского поезда 70 км/ч? Какое данное в условии задачи лишнее? <br> |
| | | | |
| - | 1523. В двоичной системе счисления при записи числа используют всего две цифры: 0 и 1. Число «один» записывается, как обычно, 1, но число «два» составляет уже единицу второго разряда и поэтому записывается так: 10<sub>2</sub> «одна двойка и нуль единиц» (цифра 2, находящаяся внизу в конце записи числа, означает, что число записано в двоичной системе). <br>Число «три» изображается: 11<sub>2</sub> «одна двойка и одна единица». Число «четыре» представляет собой единицу следующего, третьего разряда и поэтому записывается так: 100<sub>2</sub> «одна четверка, нуль двоек и нуль единиц». Таким образом, если в записи числа цифру 1 передвинуть влево на один разряд, то ее значение увеличивается вдвое (а не в десять раз, как в нашей десятичной системе). Сравните представление числа, запись которого состоит из четырех цифр 1, в виде суммы разрядных единиц в десятичной и двоичной системах: | + | 1520. Длина стороны основания пирамиды Хеопса 230 м. Туристы, осматривая пирамиду, идут со скоростью 0,32 м/с. Успеют ли туристы за час обойти ? вокруг пирамиды? <br> |
| | + | |
| | + | 1521. Заполните таблицу: <br> |
| | + | |
| | + | [[Image:17-06-207.jpg|550px|Задание]]<br> |
| | + | |
| | + | 1522. Вычислите: <br> |
| | + | |
| | + | 1) (7 -5,38) • 2,5<br> |
| | + | |
| | + | 2) (8 - 6,46) •1,5 |
| | + | |
| | + | 1523. В двоичной системе счисления при записи числа используют всего две цифры: 0 и 1. Число «один» записывается, как обычно, 1, но число «два» составляет уже единицу второго разряда и поэтому записывается так: 10<sub>2</sub> «одна двойка и нуль единиц» (цифра 2, находящаяся внизу в конце записи числа, означает, что число записано в двоичной системе). |
| | + | |
| | + | Число «три» изображается: 11<sub>2</sub> «одна двойка и одна единица». Число «четыре» представляет собой единицу следующего, третьего разряда и поэтому записывается так: 100<sub>2</sub> «одна четверка, нуль двоек и нуль единиц». |
| | + | |
| | + | Таким образом, если в записи числа цифру 1 передвинуть влево на один разряд, то ее значение увеличивается вдвое (а не в десять раз, как в нашей десятичной системе). Сравните представление числа, запись которого состоит из четырех цифр 1, в виде суммы разрядных единиц в десятичной и двоичной системах: |
| | | | |
| | 1111 = 1 • 1000 + 1 • 100 + 1 • 10 + 1 = 1 • 10<sup>3</sup> + 1 • 10<sup>2</sup> + 1 • 10 + 1; <br>1111<sub>2</sub> = 1 • 8 + 1• 4 + 1• 2 + 1 = 1• 2<sup>3</sup>+1• 2<sup>2</sup> + 1• 2 + 1 = 15. | | 1111 = 1 • 1000 + 1 • 100 + 1 • 10 + 1 = 1 • 10<sup>3</sup> + 1 • 10<sup>2</sup> + 1 • 10 + 1; <br>1111<sub>2</sub> = 1 • 8 + 1• 4 + 1• 2 + 1 = 1• 2<sup>3</sup>+1• 2<sup>2</sup> + 1• 2 + 1 = 15. |
| | | | |
| - | Попробуйте записать в десятичной системе счисления числа, которые в двоичной системе пишутся так: 102; 1002; 1012; 1102; 11102. <br>Запишите в двоичной системе все натуральные числа от 1 до 15 включительно. <br>Подумайте, почему двоичная система широко используется в вычислительной технике, но она неудобна в повседневной практике. | + | Попробуйте записать в десятичной системе счисления числа, которые в двоичной системе пишутся так: 102; 1002; 1012; 1102; 11102. |
| | + | |
| | + | Запишите в двоичной системе все натуральные числа от 1 до 15 включительно. |
| | + | |
| | + | Подумайте, почему двоичная система широко используется в [http://xvatit.com/it '''вычислительной технике'''], но она неудобна в повседневной практике. |
| | | | |
| | 1524. Найдите среднее арифметическое чисел: | | 1524. Найдите среднее арифметическое чисел: |
| Строка 159: |
Строка 177: |
| | 1534. Найдите значение выражения: | | 1534. Найдите значение выражения: |
| | | | |
| - | а) 3,4x + 5,7x + 6,6x- 4,7x при х = 3,6; 0,8; 10; <br>б) 3,8m - (2,8m + 0,7т) при m = 2,4; 8,57; <br>в) 16,75y - (4,75y+ 10,8) при у = 0,9; 3,01. <br><br>1535. Выполните действия: <br>а) 42,165 - 22,165 : (0,61 + 3,42); <br>б) 243,08 + 256,32 : (28 - 25,5). | + | а) 3,4x + 5,7x + 6,6x- 4,7x при х = 3,6; 0,8; 10; <br>б) 3,8m - (2,8m + 0,7т) при m = 2,4; 8,57; <br>в) 16,75y - (4,75y+ 10,8) при у = 0,9; 3,01. <br><br>1535. Выполните действия: |
| | | | |
| - | [[Image:17-06-208.jpg]]<br>Первыми «вычислительными устройствами», которыми пользовались в древности люди, были пальцы рук и камешки. Позднее появились бирки с зарубками <br>и веревки с узелками. <br>В Древнем Египте и Древней Греции задолго до нашей эры использовали абйк — доску с полосками, по которым передвигались камешки. Это было первое устройство, специально предназначенное для вычислений. Со временем абак совершенствовали — в римском абйке (рис. 154) камешки или шарики передвигались по желобкам (от римлян к нам перешло слово «калькуляция», означающее буквально «счет камешками»); в китайских счетах «суан-пан» {рис. 155, а) и японских «соробан» (рис. 155, б) шарики были нанизаны на прутики. Абак просуществовал до 17 века, когда его заменили письменные вычисления. Русский абак — счеты (рис. 155, в) появились в XVI веке, ими пользуются и в наши дни. Большое преимущество русских счетов в том, что они основаны на десятичной системе счисления, а не на пятеричной, как все остальные абаки. <br>Первый арифмометр, выполнявший все четыре арифметических действия, создал в 1673 году немецкий физик, изобретатель и математик '''Готфрид Вильгельм Лейбниц,''' наиболее совершенный для того времени арифмометр изобрел в 1878 году великий русский математик '''Пафнутий Львович Чебышёв.''' <br>Создание миниатюрных ЭВМ — микрокалькуляторов — стало возможно после того, как были разработаны способы изготовления электронных схем, содержа- <br>щих тысячи транзисторов и других элементов на пластинке размером с ноготь человека. С использованием микрокалькуляторов для вычислений мы познакомимся в следующем пункте учебника.
| + | а) 42,165 - 22,165 : (0,61 + 3,42); <br>б) 243,08 + 256,32 : (28 - 25,5). |
| | | | |
| - | [[Image:17-06-209.jpg]]<br><br> | + | [[Image:17-06-208.jpg|180px|Римский абак]]<br>Первыми «[http://xvatit.com/it '''вычислительными'''] устройствами», которыми пользовались в древности люди, были пальцы рук и камешки. Позднее появились бирки с зарубками и веревки с узелками. |
| | + | |
| | + | В Древнем Египте и Древней Греции задолго до нашей эры использовали абйк — доску с полосками, по которым передвигались камешки. Это было первое устройство, специально предназначенное для вычислений. Со временем абак совершенствовали — в римском абаке (рис. 154) камешки или шарики передвигались по желобкам (от римлян к нам перешло слово «калькуляция», означающее буквально «счет камешками»); в китайских счетах «суан-пан» {рис. 155, а) и японских «соробан» (рис. 155, б) шарики были нанизаны на прутики. Абак просуществовал до 17 века, когда его заменили письменные вычисления. Русский абак — счеты (рис. 155, в) появились в XVI веке, ими пользуются и в наши дни. Большое преимущество русских счетов в том, что они основаны на десятичной системе счисления, а не на пятеричной, как все остальные абаки. |
| | + | |
| | + | Первый арифмометр, выполнявший все четыре арифметических действия, создал в 1673 году немецкий физик, изобретатель и математик Готфрид Вильгельм Лейбниц, наиболее совершенный для того времени арифмометр изобрел в 1878 году великий русский [http://xvatit.com/vuzi/ '''математик'''] Пафнутий Львович Чебышёв. |
| | + | |
| | + | Создание миниатюрных ЭВМ — микрокалькуляторов — стало возможно после того, как были разработаны способы изготовления электронных схем, содержащих тысячи транзисторов и других элементов на пластинке размером с ноготь человека. С использованием микрокалькуляторов для вычислений мы познакомимся в следующем пункте учебника. |
| | + | |
| | + | [[Image:17-06-209.jpg|480px|Счеты]]<br><br> |
| | | | |
| | <br> ''Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений'' <br> | | <br> ''Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | <sub>Календарно-тематическое планирование, задачи школьнику 5 класса по математике [[Математика|скачать]], Математика [[Гипермаркет знаний - первый в мире!|онлайн]] </sub>
| |
| | | | |
| - | <br> | + | |
| | + | <sub>Календарно-тематическое планирование, задачи школьнику 5 класса по математике [[Математика|скачать]], Математика [[Гипермаркет знаний - первый в мире!|онлайн]] </sub><br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Версия 20:05, 5 октября 2012
Гипермаркет знаний>>Математика>>Математика 5 класс>>Математика:Среднее арифметическое
Среднее арифметическое
Задача 1. Миша, Коля и Петя были в походе. Подойдя к лесу, они решили сделать привал. У Миши было 2 пирожка, у Пети — 4 и у Коли — 6. Все пирожки мальчики разделили поровну и съели. Сколько пирожков съел каждый?
Решение. Всего у мальчиков было 2 + 4 + 6, то есть 12 пирожков. Каждому досталось по 12 : 3, то есть по 4 пирожка. Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых.

Задача 2. Человек шел 2 ч со скоростью 4,6 км/ч и 3 ч со скоростью 5,1 км/ч. С какой постоянной скоростью он должен был идти, чтобы пройти то же расстояние за то же время?
Решение. Найдем все расстояние, которое прошел пешеход:
4,6 • 2 + 5,1 • 3 = 9,2 + 15,3 = 24,5 (км).
Разделим полученный результат на время, затраченное на этот путь:
24,5 : 5 = 4,9. Получим ответ: пешеход должен идти с постоянной скоростью 4,9 км/ч. Такую скорость называют средней скоростью движения.

Этот же ответ можно получить, если найти среднее арифметическое скоростей за каждый час движения: (4,6 + 4,6 + 5,1 + 5,1 + 5,1) : 5 = 4,9.
Подобным образом находят среднюю урожайность, среднюю производительность и т. д.
Какое число называют средним арифметическим нескольких чисел?
Как найти среднее арифметическое нескольких чисел?
Как найти среднюю скорость движения?
1496. Найдите среднее арифметическое чисел 2 и 10. Изобразите на координатном луче число 2, число 10 и их среднее арифметическое. Сделайте вывод.
1497. Найдите среднее арифметическое чисел:
а) 70,6 и 71,3;
б) 0,1; 0,2 и 0,3;
в) 1,11; 1,12; 1,19 и 1,48;
г) 7,381; 5,004; 6,118; 8,019; 7,815 и 5,863.
1498. На рисунке 153 АВ = ВС, где А(8,9) и 5(9,5). Найдите координатуточки С. Чему равно среднее арифметическое координат точек А и С?
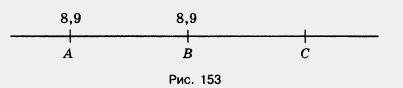
1499. Четыре поля имеют площадь по 200 га каждое. На первом поле собрали 7220 ц пшеницы, на втором — 7560 ц пшеницы, на третьем — 7090 ц пшеницы и на четвертом — 7130 ц пшеницы. Определите урожайность пшеницы на каждом поле и найдите среднюю урожайность.
1500. С поля площадью 87 га сняли урожай 10 450 ц картофеля, а с поля площадью 113 га собрали 14 980 ц картофеля. Найдите среднюю урожайность картофеля на этих полях.
1501. Найдите среднее арифметическое чисел 84,32; 84,47; 84,56 и 84,68 и округлите его до десятых.
1502. Участника соревнований пр фщур^шу катанию на коньках получила оценки 5,3; 4,8; 5,4; 5,0; 5,3; 5,4; 5,3; 5,2; 5,1. Найдите среднюю оценку этой участницы.
1503. Автомобиль двигался 3,2 ч по шоссе со скоростью 90 км/ч, затем 1,5 ч по грунтовой дороге со скоростью 45 км/ч, наконец, 0,3 ч по проселочной дороге со скоростью 30 км/ч. Найдите среднюю скорость движения автомобиля на всем пути.
1504. Поезд шел 4 ч со скоростью 70 км/ч и 3 ч со скоростью 84 км/ч. Найдите среднюю скорость поезда на пройденном за это время пути.
1505. Среднее арифметическое двух чисел равно 3,1. Одно число равно 3,8- Найдите второе число.

1506. Среднее арифметическое шести чисел равно 3,5, а среднее арифметическое четырех других чисел — 2,25. Найдите среднее арифметическое этих десяти чисел.
1507. На первом участке пути поезд шел 2 ч со скоростью 60 км/ч, а на втором он шел 3 ч. С какой скоростью шел поезд на втором участке, если его средняя скорость на двух участках была равна 51 км/ч?
1508. Скорость катера по течению 18,6 км/ч, а против течения 14,2 км/ч. Найдите собственную скорость катера и скорость течения.
1509. Одно число больше другого в 1,5 раза, среднее арифметическое этих двух чисел равно 30. Найдите эти числа.
1510. Вычислите устно:
а) 0,14 + 0,06;
2 - 0,7;
100 • 0,012;
0,42 : 7;
б) 3,18 - 1,08
2,06 + 1,04
5,4 • 0,1
4,08 : 4
в) 5,7 + 0,13
2,85 - 1,5
0,8 • 0,5
0,5 6 2
г) 0,42
0,32
0,052
0,013
1511. Выполните деление
а) 40 : 0,4;
б) 0,8 : 0,2;
в) 20 : 0,5;
г) 100 : 0,1.
д) 1000 : 0,01
е) 6 : 0,3;
ж) 0,18 : 0,6
з) 0,1 : 0,01
и) 1 : 0,5
1512. В летний лагерь детей отправляли на 6 одинаковых автобусах. В автобусах оказалось 29, 41, 28, 22, 27 и 33 человека. Можно ли было отъезжающих разместить в автобусах поровну?
1513. Вы знаете, что
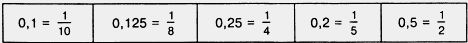
Поэтому умножить число на 0,5 означает найти половину числа, умножить на 0,125 означает найти восьмую часть числа и т. д.
Подумайте, как проще найти значение выражения:
а) 400-0,1; в) 84 • 0,25; д) 68 • 0,5.
б) 20 • 0,2; г) 16 • 0,125;
Запомните эту таблицу.
1514. Может ли произведение двух чисел оказаться меньше одного из множителей? Меньше обоих множителей? Может ли частное оказаться больше делимого? Приведите примеры.
1515. Мальчик решил определить длину моста через реку. Он заметил, что расстояние между двумя столбиками, на которых крепятся перила, равнодвум шагам, а столбиков всего 30. Какова длина моста, если один шаг мальчика 0,4 м?
1516. Выполните деление:
а) 0,432 : 0,24;
б) 0,8625 : 0,375;
в) 1,872 : 2,34;
г) 0,481 : 0,037;
д) 41,48 : 34;
е) 127,2 : 159.
1517. Решите уравнение:
а) 3,5x - 2,3x + 3,8 = 4,28; в) (8,3 - k) • 4,7 = 5,64;
б) 4,7y - (2,5у + 12,4) = 1,9; г) (9,2 - m) • 3,2 = 16.
1518. Школьная географическая площадка занимает 36 м2. Это составляет 0,1 всего пришкольного участка. Найдите площадь пришкольного участка.
1519. В 12 ч скорый поезд догнал пассажирский, а в 18 ч был уже впереди его на 120 км. Какое расстояние между поездами было в 10 ч, если скорость - пассажирского поезда 70 км/ч? Какое данное в условии задачи лишнее?
1520. Длина стороны основания пирамиды Хеопса 230 м. Туристы, осматривая пирамиду, идут со скоростью 0,32 м/с. Успеют ли туристы за час обойти ? вокруг пирамиды?
1521. Заполните таблицу:
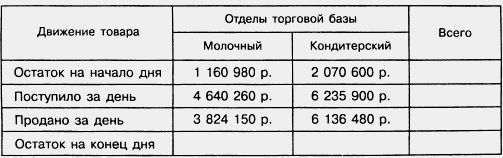
1522. Вычислите:
1) (7 -5,38) • 2,5
2) (8 - 6,46) •1,5
1523. В двоичной системе счисления при записи числа используют всего две цифры: 0 и 1. Число «один» записывается, как обычно, 1, но число «два» составляет уже единицу второго разряда и поэтому записывается так: 102 «одна двойка и нуль единиц» (цифра 2, находящаяся внизу в конце записи числа, означает, что число записано в двоичной системе).
Число «три» изображается: 112 «одна двойка и одна единица». Число «четыре» представляет собой единицу следующего, третьего разряда и поэтому записывается так: 1002 «одна четверка, нуль двоек и нуль единиц».
Таким образом, если в записи числа цифру 1 передвинуть влево на один разряд, то ее значение увеличивается вдвое (а не в десять раз, как в нашей десятичной системе). Сравните представление числа, запись которого состоит из четырех цифр 1, в виде суммы разрядных единиц в десятичной и двоичной системах:
1111 = 1 • 1000 + 1 • 100 + 1 • 10 + 1 = 1 • 103 + 1 • 102 + 1 • 10 + 1;
11112 = 1 • 8 + 1• 4 + 1• 2 + 1 = 1• 23+1• 22 + 1• 2 + 1 = 15.
Попробуйте записать в десятичной системе счисления числа, которые в двоичной системе пишутся так: 102; 1002; 1012; 1102; 11102.
Запишите в двоичной системе все натуральные числа от 1 до 15 включительно.
Подумайте, почему двоичная система широко используется в вычислительной технике, но она неудобна в повседневной практике.
1524. Найдите среднее арифметическое чисел:
а) 32,15; 31,28; 29,16; 34,54 и округлите ответ до сотых;
б) 3,234; 3,452; 4,185; 2,892 и округлите ответ до тысячных.
1525. Измерьте длину десяти своих шагов и найдите среднюю длину шага.
1526. Автомашина шла 3 ч со скоростью 53,5 км/ч, 2 ч со скоростью 62,3 км/ч и 4 ч со скоростью 48,2 км/ч. Найдите среднюю скорость движения автомашины на всем пути.
1527. Турист шел 3,8 ч со скоростью 1,2 м/с, а затем 2,2 ч со скоростью 0,9 м/с. Какова средняя скорость движения туриста на всем пути?
1528. Среднее арифметическое двух чисел 4,6. Одно число 5,4. Найдите другое число.
1529. Среднее арифметическое двух чисел 4,4. Найдите эти числа, если одно из них на 1,4 больше другого.
1530. Среднее арифметическое трех чисел 6. Найдите эти числа, если первое число в 2,5 раза больше, а второе в 1,5 раза больше третьего.
1531. За 7 ч тракторист вспахал 4,9 га. С какой скоростью двигался трактор, если ширина полосы, вспахиваемая плугами, равна 1,75 м?
1532. Для приготовления салата из зеленого лука берут 150 г зеленого лука и 30 г сметаны. Сколько сметаны потребуется повару, чтобы приготовить салат из 27 кг зеленого лука?
1533. Каждый год растительный мир дает 117 млрд т прироста массы. Каждые 3 т этой массы дают столько же энергии, сколько 1 т нефти. Сколько тонн нефти может заменить прирост массы растений за 4 года?
1534. Найдите значение выражения:
а) 3,4x + 5,7x + 6,6x- 4,7x при х = 3,6; 0,8; 10;
б) 3,8m - (2,8m + 0,7т) при m = 2,4; 8,57;
в) 16,75y - (4,75y+ 10,8) при у = 0,9; 3,01.
1535. Выполните действия:
а) 42,165 - 22,165 : (0,61 + 3,42);
б) 243,08 + 256,32 : (28 - 25,5).

Первыми «вычислительными устройствами», которыми пользовались в древности люди, были пальцы рук и камешки. Позднее появились бирки с зарубками и веревки с узелками.
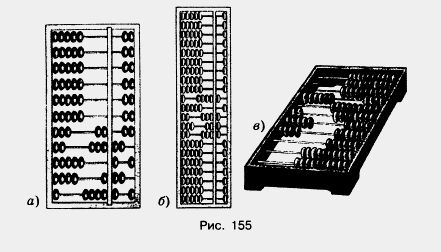
В Древнем Египте и Древней Греции задолго до нашей эры использовали абйк — доску с полосками, по которым передвигались камешки. Это было первое устройство, специально предназначенное для вычислений. Со временем абак совершенствовали — в римском абаке (рис. 154) камешки или шарики передвигались по желобкам (от римлян к нам перешло слово «калькуляция», означающее буквально «счет камешками»); в китайских счетах «суан-пан» {рис. 155, а) и японских «соробан» (рис. 155, б) шарики были нанизаны на прутики. Абак просуществовал до 17 века, когда его заменили письменные вычисления. Русский абак — счеты (рис. 155, в) появились в XVI веке, ими пользуются и в наши дни. Большое преимущество русских счетов в том, что они основаны на десятичной системе счисления, а не на пятеричной, как все остальные абаки.
Первый арифмометр, выполнявший все четыре арифметических действия, создал в 1673 году немецкий физик, изобретатель и математик Готфрид Вильгельм Лейбниц, наиболее совершенный для того времени арифмометр изобрел в 1878 году великий русский математик Пафнутий Львович Чебышёв.
Создание миниатюрных ЭВМ — микрокалькуляторов — стало возможно после того, как были разработаны способы изготовления электронных схем, содержащих тысячи транзисторов и других элементов на пластинке размером с ноготь человека. С использованием микрокалькуляторов для вычислений мы познакомимся в следующем пункте учебника.
Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Календарно-тематическое планирование, задачи школьнику 5 класса по математике скачать, Математика онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|
















