Версия 16:11, 7 октября 2012

Гіпермаркет Знань>>Математика>>Математика 7 клас. Повні уроки>> Алгебра: Графік функції

Тема

• Графік функції

Мета

• навчитися будувати графіки функції.

План

1. Визначення графіку фукції

2. Основні елементарні функції

3. Графічний спосіб задання функції

Визначення графіку фукції

Графіком функції y = f(x) називається множина всіх точок координатної площини (x, f(x)), у яких абсциси належать області визначення функції, а ординати дорівнюють відповідним значенням функції.

 

	Функцію y = f(x) називають парною, якщо для деяких значень x і (-x) з її області визначення виконується рівність f(x) = f(-x).
	Функцію y = f(x) називають непарною, якщо для деяких значень x і (-x) з її області визначення виконується рівність f(-x) = -f(x).
	Функцію y = f(x) називають зростаючою, якщо більшому значенню аргументу x відповідає більше значення функції y = f(x).
	Функцію y = f(x) називають спадною, якщо більшому значенню аргументу x відповідає менше значення функції y = f(x).
	Функцію y = f(x) називають періодичною з періодом T, якщо для будь-яких x, x + T, x - T виконується рівність f(x) = f(x + T) = f(x - T).
	Якщо в формулі y = f(x) поміняти місцями x і y, то одержимо нову функцію g(x), обернену до даної. Наприклад, оберненою до функції y = 3x - 1 є функція y = (x + 1)/3 . Графіки даної функції і функції оберненої до даної симетричні відносно прямої y = x.

Якщо при деякому x функція y = f(x) набуває найбільшого значення, то цю точку називають точкою максимуму цієї функції і позначають x_max.

Якщо в точці x = x₀ функція y = f(x) набуває найменшого значення, то цю точку називають точкою мінімуму функції і позначають x_min.
Точки максимуму і точки мінімуму називають точками екстремуму функції. Значення функції в цих точках позначають y_max і y_min.

Основні елементарні функції

	Лінійна функція має вид і її графіком є пряма лінія. Функція ні парна, ні непарна. Число називають кутовим коефіцієнтом прямої.
	Квадратична функція має вид   Її графіком є парабола з вершиною в точці з координатами:
	Показникова функція має вид   При a > 1 функція зростаюча, а при a < 1 - спадна.

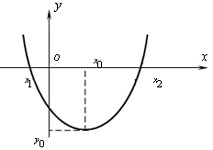
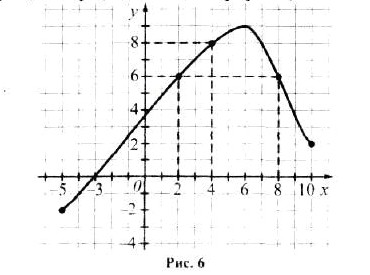
Графічний спосіб задання функції

Маючи графік функції, можна знаходити її хзначення за відомим значенням аргументу і навпаки: знаходити значення аргументу за відомим значенням функції.

Розглянемо, наприклад, функцію, графік якої зображено на рисунку 6. (Про таку функцію кажуть, що вона задана графічно).

Знайдемо за допомогою графіка значення функціх, якщо х=4. ДЛя цього через точку осі х з абсцисою 4 проведемо пряму, паралельну осі у. Точка її перетину

із графіком функції має координати (4;8). Отже, якщо х=4, то значення функції дорівнює 8. Знайдемо за допомою цього ж графіка значення аргументу, для яких значення функції дорівнює 6. Для цього через точку осі у з ординатою 6 проведемо пряму, паралельну осі х. Одержимо дві точки її перетину із графіком функції: (2;6) і (8;6). Отже, функція набуває значення 6, якщо х=2 або х=8.

Деяка лінія на координатній площині задає функцію, якщо, користуючись нею, для кожного значення змінної х можна знайти тільки одне значення змінної у.

Дивлячись на графік, зображений на рисунку 6, можна відмітити деякі властивості функції, заданої цим графіком.

1). Область визначення функції утворюють усі значення х, що задовольяють нерівності -5<=x<=10.

2). найбільше значення функції дорівнює 9 (цього значення функція набуває, якщо х=6).

3). Найменше значення функції дорівнює -2 (цього значення функція набуває, якщо х=-5).

4). Область значень функції утворюють усі значення у, що задовольняють нерівності -2<=y<=9.

5). Значення функції дорівнює нулю, якщо х=-3.Ті значення аргументу, для яких значення функції дорівнює нулю, називають нулями функції. Отже, значення х=-3 є нулем даної функції.

6). Функція набуває додатних значень, якщо -3<x<=10; від'ємних значень - якщо -5<=x<-3.
 
 

Самостійна робота

1. Побудувати графік рівняння:

1)   х-у=2;

2)   3х+4у=6;

3)   х-5у=4;

4)   3х+2у=6;

5)   2х-у=5;

6)   4х+3у=12;

7)   12у-х=4.

Список використаної літератури

1. Урок на тему «Графіки фукнцій» викладача Конченко Т. М. , Гімназії міжнародних відносин, м. Київ (СЗШ №323).
2. Істер О. А. «Алгебра. 7 клас».
3. Мерзляк А. Г., Полонський В. Б., Рабінович Ю. М., ЯкірМ. С. Збірник задачізавдань для тематичного оцінювання з алгебри для 7 класу. – Харків, Гімназія, 2004. – 112 с.: іл.

Відредаговано і надіслано Мазуренко М.С.

Над уроком працювали

Конченко Т. М.

Мазуренко М.С.

Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, но и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов  высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.

.