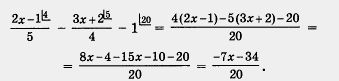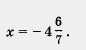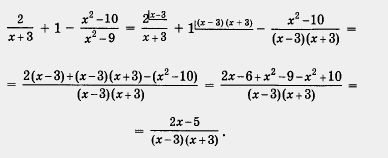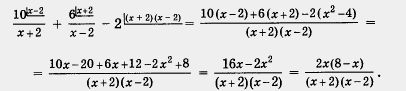|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Первые представления о решении рациональных уравнений</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Первые представления о решении рациональных уравнени, уравненией, дроби, знаменатель, преобразования, математической модели, задачи</metakeywords> |
| | | | |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Первые представления о решении рациональных уравнений''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Первые представления о решении рациональных уравнений'''<br> |
| | | | |
| - | <br> | + | <br>'''Первые представления о решении рациональных уравнений''' |
| | | | |
| | + | <br>Если р (х) — рациональное выражение, то '''[[Рівняння з двома змінними та його розв'язок. Презентація уроку|уравнение]]''' р (х) = 0 называют рациональным уравнением. Далеко не любое рациональное уравнение мы с вами сможем решить уже сейчас, для этого надо изучить другие разделы [http://xvatit.com/vuzi/ '''алгебры''']. Но справиться с некоторыми рациональными уравнениями нам уже по силам. |
| | | | |
| | + | '''Пример 1.''' Решить уравнение <br> |
| | | | |
| - | <br> '''ПЕРВЫЕ ПРЕДСТАВЛЕНИЯ О РЕШЕНИИ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ''' | + | [[Image:11-06-68.jpg|180px|Уравнение]]<br><br>Решение. Выполним действия в левой части уравнения, для чего сначала приведем имеющиеся '''[[Задачі до уроку «Додавання і віднімання звичайних дробів з однаковими знаменниками.»|дроби]]''' к общему знаменателю 20: |
| | | | |
| - | <br>Если р (х) — рациональное выражение, то уравнение р (х) = 0 называют рациональным уравнением. Далеко не любое рациональное уравнение мы с вами сможем решить уже сейчас, для этого надо изучить другие разделы алгебры. Но справиться с некоторыми рациональными уравнениями нам уже по силам. | + | [[Image:11-06-69.jpg|320px|Задание]]<br><br>Теперь заданное уравнение можно переписать в виде |
| | | | |
| - | '''Пример 1.''' Решить уравнение <br> | + | [[Image:11-06-70.jpg|Задание]]<br><br>Дробь обращается в нуль лишь при условиях, что числитель равен нулю, а '''[[Задачі до уроку на тему «Додавання і віднімання дробів з різними знаменниками»|знаменатель]]''' отличен от нуля. Значит, получаем |
| | | | |
| - | [[Image:11-06-68.jpg]]<br><br>Решение. Выполним действия в левой части уравнения, для чего сначала приведем имеющиеся дроби к общему знаменателю 20: | + | [[Image:11-06-71.jpg|320px|Задание]]<br><br>Ответ:[[Image:11-06-72.jpg|Ответ]]<br><br>'''Пример 2.''' Решить уравнение |
| | | | |
| - | [[Image:11-06-69.jpg]]<br><br>Теперь заданное уравнение можно переписать в виде | + | [[Image:11-06-73.jpg|180px|Задание]]<br><br>Решение. Равенства А = ВиА- В = 0 выражают одну и ту же зависимость между А и В. Учитывая это, перепишем данное <br>уравнение в виде |
| | | | |
| - | [[Image:11-06-70.jpg]]<br><br>Дробь обращается в нуль лишь при условиях, что числитель равен нулю, а знаменатель отличен от нуля. Значит, получаем | + | [[Image:11-06-74.jpg|180px|Задание]]<br><br>Это — рациональное уравнение. Выполним преобразования его левой части: |
| | | | |
| - | [[Image:11-06-71.jpg]]<br><br>Ответ:[[Image:11-06-72.jpg]]<br><br>'''Пример 2.''' Решить уравнение | + | [[Image:11-06-75.jpg|320px|Задание]]<br><br>В итоге мы приходим к уравнению |
| | | | |
| - | [[Image:11-06-73.jpg]]<br><br>Решение. Равенства А = ВиА- В = 0 выражают одну и ту же зависимость между А и В. Учитывая это, перепишем данное <br>уравнение в виде | + | [[Image:11-06-76.jpg|Задание]]<br><br>Снова воспользуемся условиями равенства дроби нулю (они сформулированы в ходе решения примера 1). Получаем |
| | | | |
| - | [[Image:11-06-74.jpg]]<br><br>Это — рациональное уравнение. Выполним преобразования его левой части:
| + | 2х -5 = 0; 2x = 5; x = 2,5. |
| | | | |
| - | [[Image:11-06-75.jpg]]<br><br>В итоге мы приходим к уравнению
| + | Но не забудьте, что условий равенства дроби нулю — два: равенство нулю числителя (этим мы уже воспользовались) и отличие от нуля ее знаменателя. Это второе условие надо проверить. |
| | | | |
| - | [[Image:11-06-76.jpg]]<br><br>Снова воспользуемся условиями равенства дроби нулю (они сформулированы в ходе решения примера 1). Получаем <br>2х -5 = 0; 2x = 5; x = 2,5. <br>Но не забудьте, что условий равенства дроби нулю — два: равенство нулю числителя (этим мы уже воспользовались) и отличие от нуля ее знаменателя. Это второе условие надо проверить.
| + | Если х = 2,5, то знаменатель (х - 3) (x + 3) отличен от нуля. <br> |
| | | | |
| - | Если х = 2,5, то знаменатель (х - 3) (x + 3) отличен от нуля. <br>
| + | Все в порядке, х = 2,5 — корень уравнения. <br> |
| | | | |
| - | Все в порядке, х = 2,5 — корень уравнения. <br>
| + | О т в е т: х = 2,5. <br> |
| | | | |
| - | О т в е т: х = 2,5. <br>
| + | К обоим условиям равенства дроби [[Image:11-06-77.jpg]] нулю надо относиться одинаково уважительно, т. е. сначала надо воспользоваться условием а = 0, а затем не забыть проверить условие [[Image:11-06-78.jpg]]. Решим, например, уравнение |
| | | | |
| - | К обоим условиям равенства дроби [[Image:11-06-77.jpg]] нулю надо относиться одинаково уважительно, т. е. сначала надо воспользоваться условием а = 0, а <br>затем не забыть проверить условие [[Image:11-06-78.jpg]]. Решим, например, уравнение
| + | [[Image:11-06-79.jpg|Задание]]<br><br>Приравняв числитель к нулю, получим х - 1 = 0, т. е. x = 1. Теперь подставим значение х ~ 1 в знаменатель. Получим нуль, а на нуль делить нельзя. Что это значит? Это значит, что х = 1 не является корнем уравнения, т. е. заданное уравнение вообще не имеет корней. <br><br>'''Пример 3'''. Решить уравнение [[Image:11-06-80.jpg|Задание]]. <br>Решение. Имеем |
| | | | |
| - | [[Image:11-06-79.jpg]]<br><br>Приравняв числитель к нулю, получим х - 1 = 0, т. е. x = 1. Теперь подставим значение х ~ 1 в знаменатель. Получим нуль, а на нуль делить нельзя. Что это значит? Это значит, что х = 1 не является корнем уравнения, т. е. заданное уравнение вообще не имеет корней. <br><br>'''Пример 3'''. Решить уравнение [[Image:11-06-80.jpg]]. <br>Решение. Имеем | + | [[Image:11-06-81.jpg|180px|Задание]]<br><br>Выполним '''[[Преобразование тригонометрических выражений. Основные результаты|преобразования]]''' левой части уравнения: |
| | | | |
| - | [[Image:11-06-81.jpg]]<br><br>Выполним преобразования левой части уравнения: | + | [[Image:11-06-82.jpg|420px|Задание]]<br><br>Теперь заданное уравнение можно переписать в виде |
| | | | |
| - | [[Image:11-06-82.jpg]]<br><br>Теперь заданное уравнение можно переписать в виде | + | [[Image:11-06-83.jpg|Задание]]<br><br>Первое условие равенства дроби нулю приводит к уравнению 2х (8 - х) = 0, откуда получаем 2х = 0 или 8 - х = 0, т. е. х = 0 или x = 8. |
| | | | |
| - | [[Image:11-06-83.jpg]]<br><br>Первое условие равенства дроби нулю приводит к уравнению 2х (8 - х) = 0, откуда получаем 2х = 0 или 8 - х = 0, т. е. х = 0 или x = 8.
| + | Второе условие равенства дроби нулю обязывает нас поочередно подставить найденные значения х = 0 и х = 8в знаменатель. Поскольку ни при х = 0, ни при х = 8 знаменатель не обращается в нуль, оба значения являются корнями уравнения. <br> |
| | | | |
| - | Второе условие равенства дроби нулю обязывает нас поочередно подставить найденные значения ж = 0иж = 8в знаменатель. Поскольку ни при х = 0, ни при х = 8 знаменатель не обращается в нуль, оба значения являются корнями уравнения. <br>
| + | О т в е т: 0, 8. <br> |
| | | | |
| - | О т в е т: 0, 8. <br>
| + | '''Пример 4.''' Лодка прошла 10 км по течению реки и 6 км против течения, затратив на весь путь 2 ч. Чему равна собственная скорость лодки, если скорость течения реки равна 2 км/ч? <br> |
| | | | |
| - | '''Пример 4.''' Лодка прошла 10 км по течению реки и 6 км против течения, затратив на весь путь 2 ч. Чему равна собственная скорость лодки, если скорость течения реки равна 2 км/ч? <br> | + | Решение. <br><u>'''Первый этап.'''</u> Составление '''[[Что такое математическая модель|математической модели]]'''. |
| | | | |
| - | Решение. <br><u>'''Первый этап.'''</u> Составление математической модели.
| + | Этот этап нами уже выполнен ранее — см. пример 2 из § 1. Математическая модель задачи — уравнение <br> |
| | | | |
| - | Этот этап нами уже выполнен ранее — см. пример 2 из § 1. Математическая модель задачи — уравнение <br>
| + | [[Image:11-06-84.jpg|Задание]]<br> |
| - | | + | |
| - | [[Image:11-06-84.jpg]]<br> | + | |
| | | | |
| | где х км/ч — собственная скорость лодки. | | где х км/ч — собственная скорость лодки. |
| | | | |
| - | <u>'''Второй этап.'''</u> Работа с составленной моделью. <br>В § 1 мы этого сделать не смогли. Теперь мы с вами знаем побольше, и эту модель, т. е. это уравнение, уже решили выше в примере 3. Получили х — 0 или х = 8. | + | <u>'''Второй этап.'''</u> Работа с составленной моделью. |
| | | | |
| - | <u>'''Третий этап'''</u>. Ответ на вопрос задачи. <br>Нужно выяснить, чему равна собственная скорость лодки, т. е. чему равно значение х? Мы получили, что либо х = 0, либо х = 8. Первое значение нас явно не устраивает: собственная скорость лодки не может быть равной 0 км/ч. Второе значение нас устраивает.
| + | В § 1 мы этого сделать не смогли. Теперь мы с вами знаем побольше, и эту модель, т. е. это уравнение, уже решили выше в примере 3. Получили х — 0 или х = 8. |
| | | | |
| - | Ответ: собственная скорость лодки равна 8 км/ч. <br><br><br><br><br>
| + | <u>'''Третий этап'''</u>. Ответ на вопрос '''[[Задачі до теми Розв'язування задач за допомогою рівнянь|задачи]]'''. |
| | | | |
| - | <br> | + | Нужно выяснить, чему равна собственная скорость лодки, т. е. чему равно значение х? Мы получили, что либо х = 0, либо х = 8. Первое значение нас явно не устраивает: собственная скорость лодки не может быть равной 0 км/ч. Второе значение нас устраивает. |
| | + | |
| | + | Ответ: собственная скорость лодки равна 8 км/ч. <br><br>''Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. ''<br> |
| | + | |
| | + | <br> |
| | | | |
| | <sub>Календарно-тематическое планирование по математике, видео по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub> | | <sub>Календарно-тематическое планирование по математике, видео по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub> |
| Строка 72: |
Строка 76: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 06:48, 8 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Первые представления о решении рациональных уравнений
Первые представления о решении рациональных уравнений
Если р (х) — рациональное выражение, то уравнение р (х) = 0 называют рациональным уравнением. Далеко не любое рациональное уравнение мы с вами сможем решить уже сейчас, для этого надо изучить другие разделы алгебры. Но справиться с некоторыми рациональными уравнениями нам уже по силам.
Пример 1. Решить уравнение
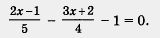
Решение. Выполним действия в левой части уравнения, для чего сначала приведем имеющиеся дроби к общему знаменателю 20:
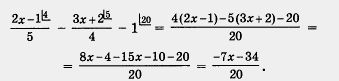
Теперь заданное уравнение можно переписать в виде
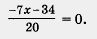
Дробь обращается в нуль лишь при условиях, что числитель равен нулю, а знаменатель отличен от нуля. Значит, получаем
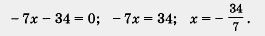
Ответ: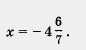
Пример 2. Решить уравнение
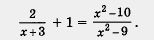
Решение. Равенства А = ВиА- В = 0 выражают одну и ту же зависимость между А и В. Учитывая это, перепишем данное
уравнение в виде
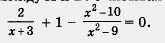
Это — рациональное уравнение. Выполним преобразования его левой части:
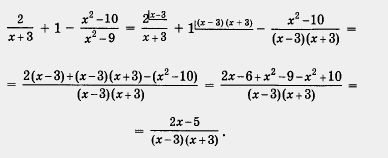
В итоге мы приходим к уравнению
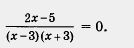
Снова воспользуемся условиями равенства дроби нулю (они сформулированы в ходе решения примера 1). Получаем
2х -5 = 0; 2x = 5; x = 2,5.
Но не забудьте, что условий равенства дроби нулю — два: равенство нулю числителя (этим мы уже воспользовались) и отличие от нуля ее знаменателя. Это второе условие надо проверить.
Если х = 2,5, то знаменатель (х - 3) (x + 3) отличен от нуля.
Все в порядке, х = 2,5 — корень уравнения.
О т в е т: х = 2,5.
К обоим условиям равенства дроби 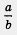 нулю надо относиться одинаково уважительно, т. е. сначала надо воспользоваться условием а = 0, а затем не забыть проверить условие нулю надо относиться одинаково уважительно, т. е. сначала надо воспользоваться условием а = 0, а затем не забыть проверить условие 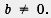 . Решим, например, уравнение . Решим, например, уравнение
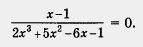
Приравняв числитель к нулю, получим х - 1 = 0, т. е. x = 1. Теперь подставим значение х ~ 1 в знаменатель. Получим нуль, а на нуль делить нельзя. Что это значит? Это значит, что х = 1 не является корнем уравнения, т. е. заданное уравнение вообще не имеет корней.
Пример 3. Решить уравнение 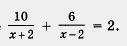 . .
Решение. Имеем
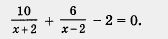
Выполним преобразования левой части уравнения:
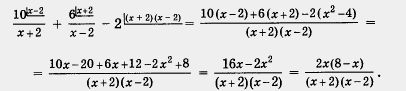
Теперь заданное уравнение можно переписать в виде
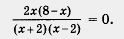
Первое условие равенства дроби нулю приводит к уравнению 2х (8 - х) = 0, откуда получаем 2х = 0 или 8 - х = 0, т. е. х = 0 или x = 8.
Второе условие равенства дроби нулю обязывает нас поочередно подставить найденные значения х = 0 и х = 8в знаменатель. Поскольку ни при х = 0, ни при х = 8 знаменатель не обращается в нуль, оба значения являются корнями уравнения.
О т в е т: 0, 8.
Пример 4. Лодка прошла 10 км по течению реки и 6 км против течения, затратив на весь путь 2 ч. Чему равна собственная скорость лодки, если скорость течения реки равна 2 км/ч?
Решение.
Первый этап. Составление математической модели.
Этот этап нами уже выполнен ранее — см. пример 2 из § 1. Математическая модель задачи — уравнение
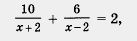
где х км/ч — собственная скорость лодки.
Второй этап. Работа с составленной моделью.
В § 1 мы этого сделать не смогли. Теперь мы с вами знаем побольше, и эту модель, т. е. это уравнение, уже решили выше в примере 3. Получили х — 0 или х = 8.
Третий этап. Ответ на вопрос задачи.
Нужно выяснить, чему равна собственная скорость лодки, т. е. чему равно значение х? Мы получили, что либо х = 0, либо х = 8. Первое значение нас явно не устраивает: собственная скорость лодки не может быть равной 0 км/ч. Второе значение нас устраивает.
Ответ: собственная скорость лодки равна 8 км/ч.
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|