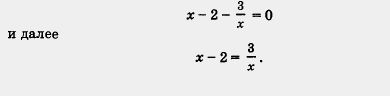|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Графическое решение квадратных уравнений</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Графическое решение квадратных уравнений, коэффициенты, алгоритмом, координатной плоскости, графики функций, уравнения, график, точки</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Графическое решение квадратных уравнений'''<br> | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Графическое решение квадратных уравнений'''<br> |
| Строка 7: |
Строка 7: |
| | '''Графическое решение квадратных уравнений''' | | '''Графическое решение квадратных уравнений''' |
| | | | |
| - | <br>С квадратными уравнениями вы уже встречались в [http://xvatit.com/vuzi/ '''курсе'''] алгебры 7-го класса. Напомним, что квадратным уравнением называют уравнение вида ах<sup>2</sup> + bх + с = 0, где а, b, с — любые числа (коэффициенты), причем а [[Image:12-06-1.jpg]]. Используя наши знания о некоторых функциях и их графиках, мы в состоянии уже теперь, не дожидаясь систематического изучения темы «Квадратные уравнения» (это будет позднее, в главе 4), решать некоторые квадратные уравнения, причем различными способами; мы рассмотрим эти способы на примере одного квадратного уравнения. | + | <br>С квадратными уравнениями вы уже встречались в [http://xvatit.com/vuzi/ '''курсе'''] алгебры 7-го класса. Напомним, что квадратным уравнением называют уравнение вида ах<sup>2</sup> + bх + с = 0, где а, b, с — любые числа ('''[[Задачі: Переставна і сполучна властивості множення. Коефіцієнт|коэффициенты]]'''), причем а [[Image:12-06-1.jpg]]. Используя наши знания о некоторых функциях и их графиках, мы в состоянии уже теперь, не дожидаясь систематического изучения темы «Квадратные уравнения» (это будет позднее, в главе 4), решать некоторые квадратные уравнения, причем различными способами; мы рассмотрим эти способы на примере одного квадратного уравнения. |
| | | | |
| - | '''Пример.''' Решить уравнение х<sup>2</sup> - 2х - 3 = 0. <br>Решение. <br><u>'''I способ'''</u>. Построим график функции у = х<sup>2</sup> - 2х - 3, воспользовавшись алгоритмом из § 13: | + | '''Пример.''' Решить уравнение х<sup>2</sup> - 2х - 3 = 0. <br>Решение. <br><u>'''I способ'''</u>. Построим график функции у = х<sup>2</sup> - 2х - 3, воспользовавшись '''[[Урок 4. Программа действий. Алгоритм|алгоритмом]]''' из § 13: |
| | | | |
| | 1) Имеем: а = 1, b = -2, х<sub>0</sub> = [[Image:12-06-2.jpg]] = 1, у<sub>0</sub> = f(1)= 1<sup>2</sup> - 2 - 3= -4. Значит, вершиной параболы служит точка (1; -4), а осью параболы — прямая х = 1. | | 1) Имеем: а = 1, b = -2, х<sub>0</sub> = [[Image:12-06-2.jpg]] = 1, у<sub>0</sub> = f(1)= 1<sup>2</sup> - 2 - 3= -4. Значит, вершиной параболы служит точка (1; -4), а осью параболы — прямая х = 1. |
| Строка 15: |
Строка 15: |
| | 2) Возьмем на оси х две точки, симметричные относительно оси параболы, например точки х = -1 и х = 3. | | 2) Возьмем на оси х две точки, симметричные относительно оси параболы, например точки х = -1 и х = 3. |
| | | | |
| - | Имеем f(-1) = f(3) = 0. Построим на координатной плоскости точки (-1; 0) и (3; 0). | + | Имеем f(-1) = f(3) = 0. Построим на '''[[Ілюстрації до теми Координатна площина|координатной плоскости]]''' точки (-1; 0) и (3; 0). |
| | | | |
| | 3) Через точки (-1; 0), (1; -4), (3; 0) проводим параболу (рис. 68). | | 3) Через точки (-1; 0), (1; -4), (3; 0) проводим параболу (рис. 68). |
| Строка 25: |
Строка 25: |
| | <br> | | <br> |
| | | | |
| - | [[Image:12-06-3.jpg|480px|Графическое решение квадратных уравнений]]<br><br><br><u>'''III способ'''</u>. Преобразуем уравнение к виду х<sup>2</sup> - 3 = 2х. Построим в одной системе координат графики функций у = х<sup>2</sup> - 3 и у = 2х (рис. 70). Они пересекаются в двух точках А(-1; - 2) и В (3; 6). Корнями уравнения являются абсциссы точек А и В, поэтому х<sub>1</sub> = - 1, х<sub>2</sub> = 3. | + | [[Image:12-06-3.jpg|480px|Графическое решение квадратных уравнений]]<br><br><br><u>'''III способ'''</u>. Преобразуем уравнение к виду х<sup>2</sup> - 3 = 2х. Построим в одной системе координат '''[[Линейная функция и ее график|графики функций]]''' у = х<sup>2</sup> - 3 и у = 2х (рис. 70). Они пересекаются в двух точках А(-1; - 2) и В (3; 6). Корнями уравнения являются абсциссы точек А и В, поэтому х<sub>1</sub> = - 1, х<sub>2</sub> = 3. |
| | | | |
| | <u>'''IV способ.'''</u> Преобразуем уравнение к виду х<sup>2</sup>-2х 4-1-4 = 0 <br>и далее <br>х<sup>2</sup> - 2х + 1 = 4, т. е. (х - IJ = 4. <br>Построим в одной системе координат параболу у = (х - 1)<sup>2</sup> и прямую y = 4 (рис. 71). Они пересекаются в двух точках А(-1; 4) и В(3; 4). Корнями уравнения служат абсциссы точек А и В, поэтому х<sub>1</sub> = -1, х<sub>2</sub> = 3. | | <u>'''IV способ.'''</u> Преобразуем уравнение к виду х<sup>2</sup>-2х 4-1-4 = 0 <br>и далее <br>х<sup>2</sup> - 2х + 1 = 4, т. е. (х - IJ = 4. <br>Построим в одной системе координат параболу у = (х - 1)<sup>2</sup> и прямую y = 4 (рис. 71). Они пересекаются в двух точках А(-1; 4) и В(3; 4). Корнями уравнения служат абсциссы точек А и В, поэтому х<sub>1</sub> = -1, х<sub>2</sub> = 3. |
| | | | |
| - | <u>'''V способ.'''</u> Разделив почленно обе части уравнения на х, получим | + | <u>'''V способ.'''</u> Разделив почленно обе части '''[[Ілюстрації до теми Рівняння. Задачі на знаходження невідомого доданка|уравнения]]''' на х, получим |
| | | | |
| | [[Image:12-06-4.jpg|480px|Графическое решение квадратных уравнений]] | | [[Image:12-06-4.jpg|480px|Графическое решение квадратных уравнений]] |
| Строка 45: |
Строка 45: |
| | Итак, квадратное уравнение х<sup>2</sup> - 2х - 3 = 0 мы решили графически пятью способами. Давайте проанализируем, в чем суть этих способов. | | Итак, квадратное уравнение х<sup>2</sup> - 2х - 3 = 0 мы решили графически пятью способами. Давайте проанализируем, в чем суть этих способов. |
| | | | |
| - | <u>'''I способ.'''</u> Строят график функции у точки его пересечения с осью х. | + | <u>'''I способ.'''</u> Строят '''[[Приклади графіків залежностей між величинами|график]]''' функции у точки его пересечения с осью х. |
| | | | |
| | <u>'''II способ.'''</u> Преобразуют уравнение к виду ах<sup>2</sup> = -bх - с, строят параболу у = ах<sup>2</sup> и прямую у = -bх - с, находят точки их пересечения (корнями уравнения служат абсциссы точек пересечения, если, разумеется, таковые имеются). | | <u>'''II способ.'''</u> Преобразуют уравнение к виду ах<sup>2</sup> = -bх - с, строят параболу у = ах<sup>2</sup> и прямую у = -bх - с, находят точки их пересечения (корнями уравнения служат абсциссы точек пересечения, если, разумеется, таковые имеются). |
| Строка 55: |
Строка 55: |
| | а (х + l)<sup>2</sup> + m = О <br>и далее <br>а (х + I) = - m | | а (х + l)<sup>2</sup> + m = О <br>и далее <br>а (х + I) = - m |
| | | | |
| - | Строят параболу у = а (х + I)<sup>2</sup> и прямую у = - m, параллельную оси х; находят точки пересечения параболы и прямой. | + | Строят параболу у = а (х + I)<sup>2</sup> и прямую у = - m, параллельную оси х; находят '''[[Точка, пряма, площина. Промінь. Відрізок. Презентація уроку|точки]]''' пересечения параболы и прямой. |
| | | | |
| | <u>'''V способ.'''</u> Преобразуют уравнение к виду | | <u>'''V способ.'''</u> Преобразуют уравнение к виду |
Текущая версия на 08:27, 8 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Графическое решение квадратных уравнений
Графическое решение квадратных уравнений
С квадратными уравнениями вы уже встречались в курсе алгебры 7-го класса. Напомним, что квадратным уравнением называют уравнение вида ах2 + bх + с = 0, где а, b, с — любые числа (коэффициенты), причем а 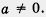 . Используя наши знания о некоторых функциях и их графиках, мы в состоянии уже теперь, не дожидаясь систематического изучения темы «Квадратные уравнения» (это будет позднее, в главе 4), решать некоторые квадратные уравнения, причем различными способами; мы рассмотрим эти способы на примере одного квадратного уравнения. . Используя наши знания о некоторых функциях и их графиках, мы в состоянии уже теперь, не дожидаясь систематического изучения темы «Квадратные уравнения» (это будет позднее, в главе 4), решать некоторые квадратные уравнения, причем различными способами; мы рассмотрим эти способы на примере одного квадратного уравнения.
Пример. Решить уравнение х2 - 2х - 3 = 0.
Решение.
I способ. Построим график функции у = х2 - 2х - 3, воспользовавшись алгоритмом из § 13:
1) Имеем: а = 1, b = -2, х0 = 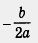 = 1, у0 = f(1)= 12 - 2 - 3= -4. Значит, вершиной параболы служит точка (1; -4), а осью параболы — прямая х = 1. = 1, у0 = f(1)= 12 - 2 - 3= -4. Значит, вершиной параболы служит точка (1; -4), а осью параболы — прямая х = 1.
2) Возьмем на оси х две точки, симметричные относительно оси параболы, например точки х = -1 и х = 3.
Имеем f(-1) = f(3) = 0. Построим на координатной плоскости точки (-1; 0) и (3; 0).
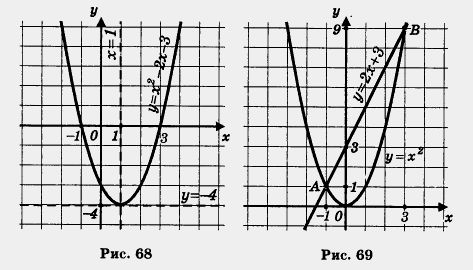
3) Через точки (-1; 0), (1; -4), (3; 0) проводим параболу (рис. 68).
Корнями уравнения х2 - 2х - 3 = 0 являются абсциссы точек пересечения параболы с осью х; значит, корни уравнения таковы: х1 = - 1, х2 — 3.
II способ. Преобразуем уравнение к виду х2 = 2х + 3. Построим в одной системе координат графики функций у — х2 и у = 2х + 3 (рис. 69). Они пересекаются в двух точках А(- 1; 1) и В(3; 9). Корнями уравнения служат абсциссы точек А и В, значит, х1 = - 1, х2 — 3.
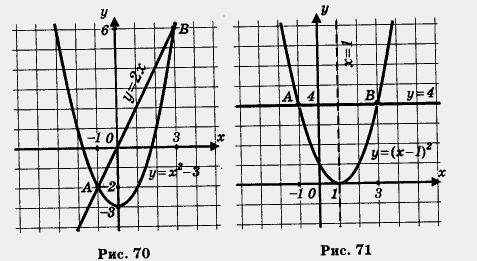
III способ. Преобразуем уравнение к виду х2 - 3 = 2х. Построим в одной системе координат графики функций у = х2 - 3 и у = 2х (рис. 70). Они пересекаются в двух точках А(-1; - 2) и В (3; 6). Корнями уравнения являются абсциссы точек А и В, поэтому х1 = - 1, х2 = 3.
IV способ. Преобразуем уравнение к виду х2-2х 4-1-4 = 0
и далее
х2 - 2х + 1 = 4, т. е. (х - IJ = 4.
Построим в одной системе координат параболу у = (х - 1)2 и прямую y = 4 (рис. 71). Они пересекаются в двух точках А(-1; 4) и В(3; 4). Корнями уравнения служат абсциссы точек А и В, поэтому х1 = -1, х2 = 3.
V способ. Разделив почленно обе части уравнения на х, получим
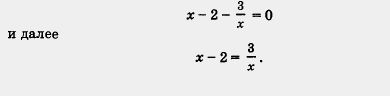
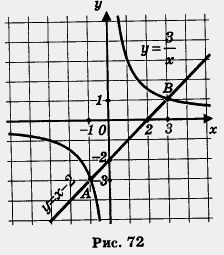
Построим в одной системе координат гиперболу 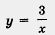 и прямую у = х - 2 (рис. 72). и прямую у = х - 2 (рис. 72).
Они пересекаются в двух точках А (-1; -3) и В(3; 1). Корнями уравнения являются абсциссы точек А и В, следовательно, х1 = - 1, х2 = 3.
Итак, квадратное уравнение х2 - 2х - 3 = 0 мы решили графически пятью способами. Давайте проанализируем, в чем суть этих способов.
I способ. Строят график функции у точки его пересечения с осью х.
II способ. Преобразуют уравнение к виду ах2 = -bх - с, строят параболу у = ах2 и прямую у = -bх - с, находят точки их пересечения (корнями уравнения служат абсциссы точек пересечения, если, разумеется, таковые имеются).
III способ. Преобразуют уравнение к виду ах2 + с = - bх,строят параболу у — ах2 + с и прямую у = -bх (она проходит через начало координат); находят точки их пересечения.
IV способ. Применяя метод выделения полного квадрата, преобразуют уравнение к виду
а (х + l)2 + m = О
и далее
а (х + I) = - m
Строят параболу у = а (х + I)2 и прямую у = - m, параллельную оси х; находят точки пересечения параболы и прямой.
V способ. Преобразуют уравнение к виду
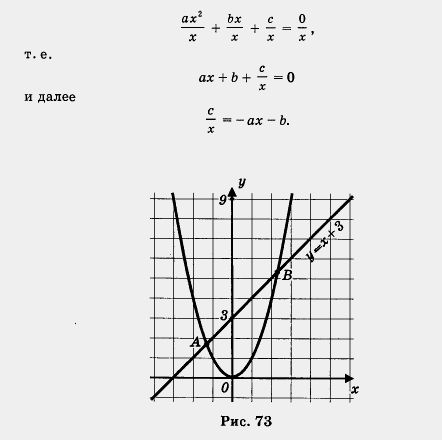
Строят гиперболу 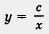 (это — гипербола при условии, что (это — гипербола при условии, что 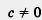 ) и прямую у = — ах — b; находят точки их пересечения. ) и прямую у = — ах — b; находят точки их пересечения.
Заметим, что первые четыре способа применимы к любым уравнениям вида ах2 + bх + с = 0, а пятый — только к тем, у которых с 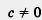 . На практике можно выбирать тот способ, который вам кажется наиболее приспособленным к данному уравнению или который вам больше нравится (или более понятен). . На практике можно выбирать тот способ, который вам кажется наиболее приспособленным к данному уравнению или который вам больше нравится (или более понятен).
Замечание. Несмотря на обилие способов графического решения квадратных уравнений, уверенности в том, что любое квадратное уравнение мы сможем решить графически, нет. Пусть, например, нужно решить уравнение х2 - х - 3 = 0 (специально возьмем уравнение, похожее на то, что было в рассмотренном примере). Попробуем его решить, например, вторым способом: преобразуем уравнение к виду х2 = х + 3, построим параболу у = х2 и
прямую у = х + 3, они пересекаются в точках А и В (рис. 73), значит, уравнение имеет два корня. Но чему равны эти корни, мы с помощью чертежа сказать не можем — точки А и В имеют не такие «хорошие» координаты, как в приведенном выше примере. А теперь рассмотрим уравнение х2- 16х— 95 = 0. Попробуем его решить, скажем, третьим способом. Преобразуем уравнение к виду х2 — 95 = 16х. Здесь надо построить параболу у = х2 - 95 и прямую у = 16х. Но ограниченные размеры листа тетради не позволяют этого сделать, ведь параболу у = х2 надо опустить на 95 клеток вниз.
Итак, графические способы решения квадратного уравнения красивы и приятны, но не дают стопроцентной гарантии решения любого квадратного уравнения. Учтем это в далнейшем.
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Математика скачать, задача школьнику 8 класса, материалы по математике для 8 класса онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|