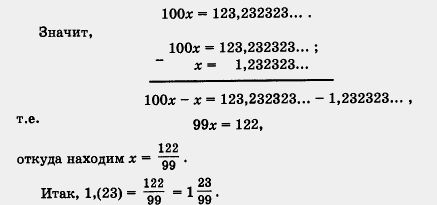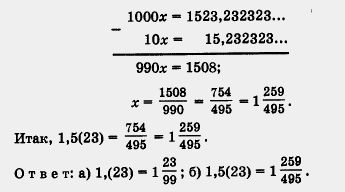|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Множество рациональных чисел</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Множество рациональных чисел, рациональных чисел, натуральные числа, дроби, множества, квадратными корнями, десятичной дроби, обыкновенную дробь</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Множество рациональных чисел''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Множество рациональных чисел''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | <br>
| + | '''Множество рациональных чисел''' |
| | | | |
| - | ''' МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ '''<br> | + | <br>В главе 3 мы убедились в том, что, кроме '''[[Конспект уроку на тему «Координатна пряма. Раціональні числа»|рациональных чисел]]''', существуют числа другой природы — к ним часто приводит операция извлечения квадратного корня (и не только она, просто мы с вами этого пока не знаем). Значит, нам нужно более обстоятельно познакомиться с новыми числами. Но сначала попробуем систематизировать наши знания о «старых», т. е. о рациональных, числах. |
| | | | |
| - | <br>В главе 3 мы убедились в том, что, кроме рациональных чисел, существуют числа другой природы — к ним часто приводит операция извлечения квадратного корня (и не только она, просто мы с вами этого пока не знаем). Значит, нам нужно более обстоятельно познакомиться с новыми числами. Но <br>сначала попробуем систематизировать наши знания о «старых», т. е. о рациональных, числах.
| |
| | | | |
| - | '''1. Некоторые символы математического языка '''<br>
| |
| | | | |
| - | Вам хорошо известны натуральные числа: <br>1, 2, 3, 4, ... <br>Множество всех натуральных чисел обычно обозначают буквой N. <br>Если к натуральным числам присоединить число 0 и все целые отрицательные числа: -1,-2,-3,-4, ..., — то получится множество целых чисел. Это множество обычно обозначают буквой Z. <br>Если к множеству целых чисел присоединить все обыкновенные дроби: [[Image:14-06-97.jpg]] и т. д., — то получится множество рацинальных чисел. Это множество обычно обозначают буквой Q. <br>Любое целое число m можно записать в виде дроби [[Image:14-06-98.jpg]] , поэтому справедливо утверждение о том, что множество Q рациональных чисел — это множество, состоящее из чисел вида [[Image:14-06-99.jpg]]<br>Используя введенные обозначения N, Z, Q, условимся о следующем: <br>1. Вместо фразы «n — натуральное число» можно писать [[Image:14-06-100.jpg]] (читается: «элемент n принадлежит множеству N»), Математический символ [[Image:14-06-112.jpg]] называют знаком принадлежности. <br>2. Вместо фразы «m — целое число» можно писать m [[Image:14-06-112.jpg]] Z. <br>3. Вместо фразы «r — рациональное число» можно писать r[[Image:14-06-112.jpg]]Q. <br>Понятно, что N — часть множества Z, а Z — часть множества Q. Для описания этой ситуации в математике также имеется специальное обозначение: <br>[[Image:14-06-102.jpg]]<br>Математический символ с называют знаком включения (одного множества в другое). <br>Вообще, в математике запись х[[Image:14-06-112.jpg]] X означает, что х — один из элементов множества X. Запись [[Image:14-06-103.jpg]] означает, что множество А представляет собой часть множества В. Математики чаще говорят так: А — подмножество множества
| + | <u>'''1. Некоторые символы математического языка'''</u><br> |
| | | | |
| - | Обратите внимание: множества в математике обычно обозначают прописными буквами, а элементы множества — строчными буквами. <br>И еще на один момент обратите внимание: знаки принадлежности (элемент принадлежит множеству) и включения (одно множество содержится в другом) — различные, соответственно [[Image:14-06-104.jpg]]<br>А как записать, что элемент х не принадлежит множеству X или что множество А не является частью (подмножеством) множества В? Используют те же символы, но перечеркнутые косой чертой: [[Image:14-06-105.jpg]]. <br>Приведем несколько примеров использования введенных математических символов для сокращения записи верных математических утверждений — их называют также истинными высказываниями.
| + | Вам хорошо известны '''[[Обозначение натуральных чисел|натуральные числа]]''': 1, 2, 3, 4, ... |
| | | | |
| - | [[Image:14-06-106.jpg]]<br><br>'''2. Рациональные числа как бесконечные десятичные периодические дроби'''
| + | Множество всех натуральных чисел обычно обозначают буквой N. |
| | | | |
| - | К рациональным числам, как мы уже не раз подчеркивали, относятся все те числа, с которыми вы успешно оперировали до тех пор, пока не встретились с квадратными корнями. <br>Это были целые числа, обыкновенные дроби, десятичные дроби. <br>Для всех этих чисел можно использовать один и тот же способ записи, который мы сейчас и обсудим. <br>Рассмотрим, например, целое число 5, обыкновенную дробь [[Image:14-06-107.jpg]] и десятичную дробь 8,377. Целое число 5 можно записать в виде бесконечной десятичной дроби: 5,0000... Десятичную дробь 8,377 также можно записать в виде бесконечной десятичной дроби: 8,377000... Для числа [[Image:14-06-107.jpg]] воспользуемся методом <br>«деления углом»:
| + | Если к натуральным числам присоединить число 0 и все целые отрицательные числа: -1,-2,-3,-4, ..., — то получится множество целых чисел. Это множество обычно обозначают буквой Z. |
| | | | |
| - | [[Image:14-06-108.jpg]]<br><br>Как видите, начиная со второй цифры после запятой происходит повторение одной и той же группы цифр: 18, 18, 18, ... . Таким образом, <br>[[Image:14-06-107.jpg]] = 0,3181818... . Короче это записывают так: 0,3(18). Повторяющуюся группу цифр после запятой называют периодом, а саму десятичную дробь — бесконечной десятичной периодической дробью. <br>бесконечной десятичной периодической дроби. Для этого надо в периоде записать число 0: <br>5 = 5,00000... = 5,(0). Так же обстоит дело и с числом 8,377: 8,377 = 8,377000... = 8,377(0). <br>Чтобы все было аккуратно, говорят так: 8,377 — конечная десятичная дробь, а 8,377000... — бесконечная десятичная дробь. <br>Таким образом, и число 5, и число [[Image:14-06-107.jpg]] , и число 8,377 удалось записать в виде бесконечной десятичной периодической дроби. <br>Вообще, любое рациональное число можно записать в виде бесконечной десятичной периодической дроби. <br>
| + | Если к множеству целых чисел присоединить все обыкновенные дроби: [[Image:14-06-97.jpg|80px|Дроби]] и т. д., — то получится множество рациональных чисел. Это множество обычно обозначают буквой Q. |
| | | | |
| - | '''''Замечание.''''' Этот вывод удобен для теории, но не очень удобен для практики. Ведь если дана конечная десятичная дробь 8,377, то зачем нужна <br>ее запись в виде 8,377(0)? Поэтому обычно говорят так: любое рациональное число можно записать в виде конечной десятичной дроби или в виде бесконеч- <br>ной десятичной периодической дроби. <br>Выше мы показали, как обыкновенную дробь представляют в виде бесконечной периодической десятичной дроби. Верно и обратное: любую бесконечную десятичную периодическую дробь можно представить в виде обыкновенной дроби. Это значит, что любая бесконечная десятичная периодическая дробь есть <br>рациональное число. <br>Покажем на примере, как бесконечную десятичную периодическую дробь превращают в обыкновенную дробь. <br> | + | Любое целое число m можно записать в виде '''[[Фішки для допитливих до уроку: Дробові числа. Звичайні дроби.|дроби]]''' [[Image:14-06-98.jpg]] , поэтому справедливо утверждение о том, что множество Q рациональных чисел — это ножество, состоящее из чисел вида [[Image:14-06-99.jpg|Числа]]<br><u>Используя введенные обозначения N, Z, Q, условимся о следующем: </u> |
| | | | |
| - | '''Пример'''. Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь: а) 1,(23); б) 1,5(23). <br>Решение, а) Положим х = 1,(23), т. е. х = 1,232323... . <br>Умножим х на такое число, чтобы запятая передвинулась вправо ровно на один период. Поскольку в периоде содержатся две цифры, нужно, чтобы запятая передвинулась вправо на две цифры, а для этого число х надо умножить на 100.<br>
| + | 1. Вместо фразы «n — натуральное число» можно писать [[Image:14-06-100.jpg]] (читается: «элемент n принадлежит множеству N»), Математический символ [[Image:14-06-112.jpg]] называют знаком принадлежности. <br>2. Вместо фразы «m — целое число» можно писать m [[Image:14-06-112.jpg]] Z. <br>3. Вместо фразы «r — рациональное число» можно писать r[[Image:14-06-112.jpg]]Q. <br>Понятно, что N — часть множества Z, а Z — часть множества Q. Для описания этой ситуации в математике также имеется специальное обозначение: [[Image:14-06-102.jpg|80px|Обозначение]] |
| | | | |
| - | Получим <br>
| + | Математический символ с называют знаком включения (одного множества в другое). |
| | | | |
| - | [[Image:14-06-109.jpg]]<br><br>б) Положим х = 1,5(23) = 1,5232323... . Сначала умножим х на 10, чтобы в полученном произведении период начинался сразу после запятой: 10х = 15,232323... . Теперь число 10х умножим на 100 — тогда запятая сместится ровно на один период вправо: 1000х - 1523,232323... . Имеем | + | Вообще, в математике запись х[[Image:14-06-112.jpg]] X означает, что х — один из элементов множества X. Запись [[Image:14-06-103.jpg|Множество]] означает, что множество А представляет собой часть '''[[Множество действительных чисел|множества]]''' В. Математики чаще говорят так: А — подмножество множества |
| | | | |
| - | [[Image:14-06-110.jpg]]<br> <br>Теперь мы сформулируем основной результат этого параграфа: множество Q рациональных чисел можно рассматривать как множество чисел вида [[Image:14-06-111.jpg]],
| + | Обратите внимание: множества в математике обычно обозначают прописными буквами, а элементы множества — строчными буквами. |
| | | | |
| - | где m — целое число, n — натуральное число, или как множество бесконечных десятичных периодических дробей. <br><br><br> | + | И еще на один момент обратите внимание: знаки принадлежности (элемент принадлежит множеству) и включения (одно множество содержится в другом) — различные, соответственно [[Image:14-06-104.jpg|Множество]] |
| | + | |
| | + | А как записать, что элемент х не принадлежит множеству X или что множество А не является частью (подмножеством) множества В? Используют те же символы, но перечеркнутые косой чертой: [[Image:14-06-105.jpg|80px|Символы]]. |
| | + | |
| | + | Приведем несколько примеров использования введенных математических символов для сокращения записи верных математических утверждений — их называют также истинными высказываниями. |
| | + | |
| | + | [[Image:14-06-106.jpg|320px|Примеры]]<br><br><u>'''2. Рациональные числа как бесконечные десятичные периодические дроби'''</u> |
| | + | |
| | + | К рациональным числам, как мы уже не раз подчеркивали, относятся все те числа, с которыми вы успешно оперировали до тех пор, пока не встретились с '''[[Квадратний корінь. Арифметичний квадратний корінь.|квадратными корнями]]'''. |
| | + | |
| | + | Это были целые числа, обыкновенные дроби, десятичные дроби. |
| | + | |
| | + | Для всех этих чисел можно использовать один и тот же способ записи, который мы сейчас и обсудим. <br>Рассмотрим, например, целое число 5, обыкновенную дробь [[Image:14-06-107.jpg]] и десятичную дробь 8,377. Целое число 5 можно записать в виде бесконечной десятичной дроби: 5,0000... Десятичную дробь 8,377 также можно записать в виде бесконечной '''[[Задачі до уроку «Порівняння десяткових дробів.»|десятичной дроби]]''': 8,377000... Для числа [[Image:14-06-107.jpg]] воспользуемся методом «деления углом»: |
| | + | |
| | + | [[Image:14-06-108.jpg|240px|Деления углом]]<br>Как видите, начиная со второй цифры после запятой происходит повторение одной и той же группы цифр: 18, 18, 18, ... . Таким образом, [[Image:14-06-107.jpg]] = 0,3181818... . Короче это записывают так: 0,3(18). Повторяющуюся группу цифр после запятой называют периодом, а саму десятичную дробь — бесконечной десятичной периодической дробью. <br>бесконечной десятичной периодической дроби. Для этого надо в периоде записать число 0: |
| | + | |
| | + | 5 = 5,00000... = 5,(0). Так же обстоит дело и с числом 8,377: 8,377 = 8,377000... = 8,377(0). |
| | + | |
| | + | Чтобы все было аккуратно, говорят так: 8,377 — конечная десятичная дробь, а 8,377000... — бесконечная десятичная дробь. <br>Таким образом, и число 5, и число [[Image:14-06-107.jpg]] , и число 8,377 удалось записать в виде бесконечной десятичной периодической дроби. |
| | + | |
| | + | Вообще, любое рациональное число можно записать в виде бесконечной десятичной периодической дроби. <br> |
| | + | |
| | + | '''''Замечание.''''' Этот вывод удобен для теории, но не очень удобен для практики. Ведь если дана конечная десятичная дробь 8,377, то зачем нужна ее запись в виде 8,377(0)? Поэтому обычно говорят так: любое рациональное число можно записать в виде конечной десятичной дроби или в виде бесконечной десятичной периодической дроби. |
| | + | |
| | + | Выше мы показали, как '''[[Задачі до уроку «Додавання і віднімання звичайних дробів з однаковими знаменниками.»|обыкновенную дробь]]''' представляют в виде бесконечной периодической десятичной дроби. Верно и обратное: любую бесконечную десятичную периодическую дробь можно представить в виде обыкновенной дроби. Это значит, что любая бесконечная десятичная периодическая дробь есть <br>рациональное число. |
| | + | |
| | + | Покажем на примере, как бесконечную десятичную периодическую дробь превращают в обыкновенную дробь. <br> |
| | + | |
| | + | '''Пример'''. Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь: а) 1,(23); б) 1,5(23). |
| | + | |
| | + | Решение, а) Положим х = 1,(23), т. е. х = 1,232323... . |
| | + | |
| | + | Умножим х на такое число, чтобы запятая передвинулась вправо ровно на один период. Поскольку в периоде содержатся две цифры, нужно, чтобы запятая передвинулась вправо на две цифры, а для этого число х надо умножить на 100.<br> |
| | + | |
| | + | Получим <br> |
| | + | |
| | + | [[Image:14-06-109.jpg|480px|Решение]]<br><br>б) Положим х = 1,5(23) = 1,5232323... . Сначала умножим х на 10, чтобы в полученном произведении период начинался сразу после запятой: 10х = 15,232323... . Теперь число 10х умножим на 100 — тогда запятая сместится ровно на один период вправо: 1000х - 1523,232323... . Имеем |
| | + | |
| | + | [[Image:14-06-110.jpg|320px|Решение]]<br> <br>Теперь мы сформулируем основной результат этого параграфа: множество Q рациональных чисел можно рассматривать как множество чисел вида [[Image:14-06-111.jpg]],где m — целое число, n — натуральное число, или как множество бесконечных десятичных периодических дробей. <br>''<br>Мордкович А. Г., [http://xvatit.com/vuzi/ '''Алгебра''']. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. ''<br> |
| | | | |
| | <br> | | <br> |
| Строка 42: |
Строка 78: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 13:23, 8 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Множество рациональных чисел
Множество рациональных чисел
В главе 3 мы убедились в том, что, кроме рациональных чисел, существуют числа другой природы — к ним часто приводит операция извлечения квадратного корня (и не только она, просто мы с вами этого пока не знаем). Значит, нам нужно более обстоятельно познакомиться с новыми числами. Но сначала попробуем систематизировать наши знания о «старых», т. е. о рациональных, числах.
1. Некоторые символы математического языка
Вам хорошо известны натуральные числа: 1, 2, 3, 4, ...
Множество всех натуральных чисел обычно обозначают буквой N.
Если к натуральным числам присоединить число 0 и все целые отрицательные числа: -1,-2,-3,-4, ..., — то получится множество целых чисел. Это множество обычно обозначают буквой Z.
Если к множеству целых чисел присоединить все обыкновенные дроби: 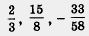 и т. д., — то получится множество рациональных чисел. Это множество обычно обозначают буквой Q. и т. д., — то получится множество рациональных чисел. Это множество обычно обозначают буквой Q.
Любое целое число m можно записать в виде дроби 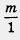 , поэтому справедливо утверждение о том, что множество Q рациональных чисел — это ножество, состоящее из чисел вида , поэтому справедливо утверждение о том, что множество Q рациональных чисел — это ножество, состоящее из чисел вида 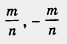
Используя введенные обозначения N, Z, Q, условимся о следующем:
1. Вместо фразы «n — натуральное число» можно писать 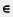 (читается: «элемент n принадлежит множеству N»), Математический символ (читается: «элемент n принадлежит множеству N»), Математический символ 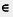 называют знаком принадлежности. называют знаком принадлежности.
2. Вместо фразы «m — целое число» можно писать m 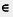 Z. Z.
3. Вместо фразы «r — рациональное число» можно писать r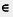 Q. Q.
Понятно, что N — часть множества Z, а Z — часть множества Q. Для описания этой ситуации в математике также имеется специальное обозначение: 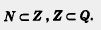
Математический символ с называют знаком включения (одного множества в другое).
Вообще, в математике запись х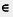 X означает, что х — один из элементов множества X. Запись X означает, что х — один из элементов множества X. Запись 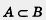 означает, что множество А представляет собой часть множества В. Математики чаще говорят так: А — подмножество множества означает, что множество А представляет собой часть множества В. Математики чаще говорят так: А — подмножество множества
Обратите внимание: множества в математике обычно обозначают прописными буквами, а элементы множества — строчными буквами.
И еще на один момент обратите внимание: знаки принадлежности (элемент принадлежит множеству) и включения (одно множество содержится в другом) — различные, соответственно 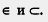
А как записать, что элемент х не принадлежит множеству X или что множество А не является частью (подмножеством) множества В? Используют те же символы, но перечеркнутые косой чертой: 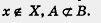 . .
Приведем несколько примеров использования введенных математических символов для сокращения записи верных математических утверждений — их называют также истинными высказываниями.

2. Рациональные числа как бесконечные десятичные периодические дроби
К рациональным числам, как мы уже не раз подчеркивали, относятся все те числа, с которыми вы успешно оперировали до тех пор, пока не встретились с квадратными корнями.
Это были целые числа, обыкновенные дроби, десятичные дроби.
Для всех этих чисел можно использовать один и тот же способ записи, который мы сейчас и обсудим.
Рассмотрим, например, целое число 5, обыкновенную дробь 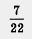 и десятичную дробь 8,377. Целое число 5 можно записать в виде бесконечной десятичной дроби: 5,0000... Десятичную дробь 8,377 также можно записать в виде бесконечной десятичной дроби: 8,377000... Для числа и десятичную дробь 8,377. Целое число 5 можно записать в виде бесконечной десятичной дроби: 5,0000... Десятичную дробь 8,377 также можно записать в виде бесконечной десятичной дроби: 8,377000... Для числа 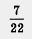 воспользуемся методом «деления углом»: воспользуемся методом «деления углом»:

Как видите, начиная со второй цифры после запятой происходит повторение одной и той же группы цифр: 18, 18, 18, ... . Таким образом, 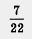 = 0,3181818... . Короче это записывают так: 0,3(18). Повторяющуюся группу цифр после запятой называют периодом, а саму десятичную дробь — бесконечной десятичной периодической дробью. = 0,3181818... . Короче это записывают так: 0,3(18). Повторяющуюся группу цифр после запятой называют периодом, а саму десятичную дробь — бесконечной десятичной периодической дробью.
бесконечной десятичной периодической дроби. Для этого надо в периоде записать число 0:
5 = 5,00000... = 5,(0). Так же обстоит дело и с числом 8,377: 8,377 = 8,377000... = 8,377(0).
Чтобы все было аккуратно, говорят так: 8,377 — конечная десятичная дробь, а 8,377000... — бесконечная десятичная дробь.
Таким образом, и число 5, и число 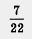 , и число 8,377 удалось записать в виде бесконечной десятичной периодической дроби. , и число 8,377 удалось записать в виде бесконечной десятичной периодической дроби.
Вообще, любое рациональное число можно записать в виде бесконечной десятичной периодической дроби.
Замечание. Этот вывод удобен для теории, но не очень удобен для практики. Ведь если дана конечная десятичная дробь 8,377, то зачем нужна ее запись в виде 8,377(0)? Поэтому обычно говорят так: любое рациональное число можно записать в виде конечной десятичной дроби или в виде бесконечной десятичной периодической дроби.
Выше мы показали, как обыкновенную дробь представляют в виде бесконечной периодической десятичной дроби. Верно и обратное: любую бесконечную десятичную периодическую дробь можно представить в виде обыкновенной дроби. Это значит, что любая бесконечная десятичная периодическая дробь есть
рациональное число.
Покажем на примере, как бесконечную десятичную периодическую дробь превращают в обыкновенную дробь.
Пример. Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь: а) 1,(23); б) 1,5(23).
Решение, а) Положим х = 1,(23), т. е. х = 1,232323... .
Умножим х на такое число, чтобы запятая передвинулась вправо ровно на один период. Поскольку в периоде содержатся две цифры, нужно, чтобы запятая передвинулась вправо на две цифры, а для этого число х надо умножить на 100.
Получим
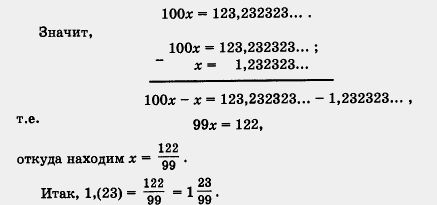
б) Положим х = 1,5(23) = 1,5232323... . Сначала умножим х на 10, чтобы в полученном произведении период начинался сразу после запятой: 10х = 15,232323... . Теперь число 10х умножим на 100 — тогда запятая сместится ровно на один период вправо: 1000х - 1523,232323... . Имеем
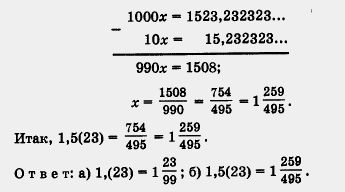
Теперь мы сформулируем основной результат этого параграфа: множество Q рациональных чисел можно рассматривать как множество чисел вида 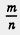 ,где m — целое число, n — натуральное число, или как множество бесконечных десятичных периодических дробей. ,где m — целое число, n — натуральное число, или как множество бесконечных десятичных периодических дробей.
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|