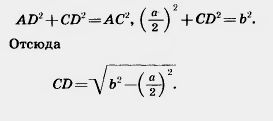|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | '''ТЕОРЕМА ПИФАГОРА'''
| + | '''Теорема Пифагора''' |
| | | | |
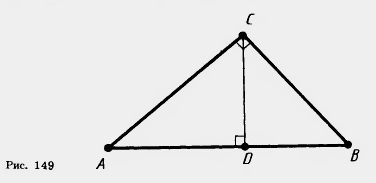
| - | <br>Теорема 7.2 (теорема Пифагора). '''''В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.'''''<br>Доказательство. Пусть ABC — данный прямоугольный треугольник с прямым углом С. Проведем высоту CD из вершины прямого угла С (рис. 149). | + | <br>'''Теорема 7.2 '''(теорема Пифагора). В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. |
| | | | |
| - | <br>[[Image:22-06-39.jpg]] <br><br>По определению косинуса угла [[Image:22-06-40.jpg]] Отсюда AB'''. '''AD=AC<sup>2</sup>. Аналогично [[Image:22-06-41.jpg]] Отсюда AB'''.'''BD=ВС<sup>2</sup>. Складывая полученные равенства почленно и замечая, что AD + DB=AB, получим:<br><br>АС<sup>2</sup> + ВС<sup>2</sup> = АВ {AD + DB) = АВ<sup>2</sup>.<br><br>Теорема доказана.
| + | Доказательство. Пусть ABC — данный прямоугольный треугольник с прямым углом С. Проведем высоту CD из вершины прямого угла С (рис. 149). |
| | | | |
| - | Из теоремы Пифагора следует, что в прямоугольном треугольнике любой из катетов меньше гипотенузы. Отсюда, в свою очередь, следует, что cos а < 1 для любого острого угла а.
| + | <br>[[Image:22-06-39.jpg|320px|Теорема Пифагора]] <br><br>По определению косинуса угла [[Image:22-06-40.jpg|140px|Косинус угла]] Отсюда AB'''. '''AD=AC<sup>2</sup>. Аналогично [[Image:22-06-41.jpg|140px|Косинус угла]] Отсюда AB'''.'''BD=ВС<sup>2</sup>. Складывая полученные равенства почленно и замечая, что AD + DB=AB, получим:<br><br>АС<sup>2</sup> + ВС<sup>2</sup> = АВ {AD + DB) = АВ<sup>2</sup>.<br><br>Теорема доказана. |
| | | | |
| - | Задача (11). Найдите медиану равнобедренного треугольника с основанием а и боковой стороной b, проведенную к основанию.<br> <br>Решение. Пусть ABC — равнобедренный треугольник с основанием АВ и CD — его медиана, проведенная к основанию (рис. 150).
| + | Из теоремы Пифагора следует, что в прямоугольном треугольнике любой из катетов меньше гипотенузы. Отсюда, в свою очередь, следует, что cos а < 1 для любого острого угла а. |
| | | | |
| | + | '''Задача (11).''' Найдите медиану равнобедренного треугольника с основанием а и боковой стороной b, проведенную к основанию. |
| | | | |
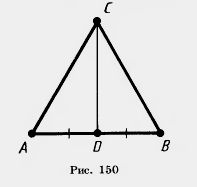
| | + | '''Решение.''' Пусть ABC — равнобедренный треугольник с основанием АВ и CD — его медиана, проведенная к основанию (рис. 150).<br> |
| | | | |
| - | [[Image:22-06-42.jpg]] | + | [[Image:22-06-42.jpg|240px|Равнобедренный треугольник ]] |
| | | | |
| | + | <br> |
| | | | |
| | + | Как мы знаем, медиана равнобедренного треугольника, проведенная к основанию, является высотой. Поэтому треугольник ACD прямоугольный с прямым углом D. По теореме Пифагора<br> |
| | | | |
| - | Как мы знаем, медиана равнобедренного треугольника, проведенная к основанию, является высотой. Поэтому треугольник ACD прямоугольный с прямым углом D. По теореме Пифагора
| + | [[Image:22-06-43.jpg|240px|Теорема Пифагора]]<br><br> |
| | | | |
| | + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ '''Геометрия'''] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| | | | |
| - | [[Image:22-06-43.jpg]]<br><br>
| |
| - |
| |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Математика для 8 класса, учебники и книги по математике [[Математика|скачать]], библиотека [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> | | <sub>Математика для 8 класса, учебники и книги по математике [[Математика|скачать]], библиотека [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> |
| Строка 34: |
Строка 36: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Доказательство. Пусть ABC — данный прямоугольный треугольник с прямым углом С. Проведем высоту CD из вершины прямого угла С (рис. 149).
Из теоремы Пифагора следует, что в прямоугольном треугольнике любой из катетов меньше гипотенузы. Отсюда, в свою очередь, следует, что cos а < 1 для любого острого угла а.
Как мы знаем, медиана равнобедренного треугольника, проведенная к основанию, является высотой. Поэтому треугольник ACD прямоугольный с прямым углом D. По теореме Пифагора
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.