|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Неравенство треугольника</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Неравенство треугольника, точки, теоремы, треугольника</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Неравенство треугольника''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Неравенство треугольника''' |
| Строка 7: |
Строка 7: |
| | '''Неравенство треугольника''' | | '''Неравенство треугольника''' |
| | | | |
| - | <br>Если точки А и В различны, то расстоянием между ними называется длина отрезка АВ. Если точки А и B совпадают, то расстояние между ними принимается равным нулю. | + | <br>Если [[Точки і прямі, їх властивості. Закриті вправи|точки]] А и В различны, то расстоянием между ними называется длина отрезка АВ. Если точки А и B совпадают, то расстояние между ними принимается равным нулю. |
| | | | |
| | '''Теорема 7.3''' (неравенство треугольника). Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей точки. | | '''Теорема 7.3''' (неравенство треугольника). Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей точки. |
| Строка 13: |
Строка 13: |
| | Это значит, что каждое из этих расстояний меньше суммы или равно сумме двух других. | | Это значит, что каждое из этих расстояний меньше суммы или равно сумме двух других. |
| | | | |
| - | Доказательство. Пусть А, В, С — три данные точки. Если две точки из трех или все три точки совпадают, то утверждение теоремы очевидно. | + | Доказательство. Пусть А, В, С — три данные точки. Если две точки из трех или все три точки совпадают, то утверждение [[Теоремы и доказательства. Полные уроки|теоремы]] очевидно. |
| | | | |
| | Если все точки различны и лежат на одной прямой, то одна из них лежит между двумя другими, например В. В этом случае АВ + ВС = АС. Отсюда видно, что каждое из трех расстояний не больше суммы двух других. | | Если все точки различны и лежат на одной прямой, то одна из них лежит между двумя другими, например В. В этом случае АВ + ВС = АС. Отсюда видно, что каждое из трех расстояний не больше суммы двух других. |
| Строка 21: |
Строка 21: |
| | Задача (23). Докажите, что любая хорда окружности не больше диаметра и равна диаметру только тогда, когда сама является диаметром. | | Задача (23). Докажите, что любая хорда окружности не больше диаметра и равна диаметру только тогда, когда сама является диаметром. |
| | | | |
| - | Решение (рис. 155). По неравенству треугольника AB[[Image:22-06-49.jpg]]OA + OB = 2R, причем если центр О не лежит на отрезке АВ, то неравенство строгое. Равенство имеет место только в случае, когда хорда проходит через центр, т. е. является диаметром. <br> | + | Решение (рис. 155). По неравенству [[Треугольник. Полные уроки|треугольника]] AB[[Image:22-06-49.jpg]]OA + OB = 2R, причем если центр О не лежит на отрезке АВ, то неравенство строгое. Равенство имеет место только в случае, когда хорда проходит через центр, т. е. является диаметром. <br> |
| - | | + | |
| - | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ '''Геометрия'''] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| + | |
| | | | |
| | + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| | + | <br> |
| | | | |
| | <sub>Рефераты, домашняя работа по математике [[Математика|скачать]], учебники скатать бесплатно, [[Гипермаркет знаний - первый в мире!|онлайн]] уроки, вопросы и ответы</sub> | | <sub>Рефераты, домашняя работа по математике [[Математика|скачать]], учебники скатать бесплатно, [[Гипермаркет знаний - первый в мире!|онлайн]] уроки, вопросы и ответы</sub> |
Текущая версия на 11:01, 9 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Неравенство треугольника
Неравенство треугольника
Если точки А и В различны, то расстоянием между ними называется длина отрезка АВ. Если точки А и B совпадают, то расстояние между ними принимается равным нулю.
Теорема 7.3 (неравенство треугольника). Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей точки.
Это значит, что каждое из этих расстояний меньше суммы или равно сумме двух других.
Доказательство. Пусть А, В, С — три данные точки. Если две точки из трех или все три точки совпадают, то утверждение теоремы очевидно.
Если все точки различны и лежат на одной прямой, то одна из них лежит между двумя другими, например В. В этом случае АВ + ВС = АС. Отсюда видно, что каждое из трех расстояний не больше суммы двух других.
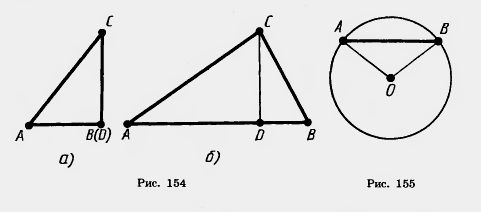
Допустим теперь, что точки не лежат на одной прямой (рис. 154). Докажем, что АВ<АС + ВС. Опустим перпендикуляр CD на прямую АВ. По доказанному AB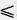 AD + BD. И так как AD<AC и BD<BC, то АВ<АС+ВС. Теорема доказана. AD + BD. И так как AD<AC и BD<BC, то АВ<АС+ВС. Теорема доказана.
Заметим, что в случае, когда точки не лежат на одной прямой, в неравенстве треугольника строгое неравенство. Отсюда следует, что в любом треугольнике каждая сторона меньше суммы двух других сторон.
Задача (23). Докажите, что любая хорда окружности не больше диаметра и равна диаметру только тогда, когда сама является диаметром.
Решение (рис. 155). По неравенству треугольника AB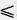 OA + OB = 2R, причем если центр О не лежит на отрезке АВ, то неравенство строгое. Равенство имеет место только в случае, когда хорда проходит через центр, т. е. является диаметром. OA + OB = 2R, причем если центр О не лежит на отрезке АВ, то неравенство строгое. Равенство имеет место только в случае, когда хорда проходит через центр, т. е. является диаметром.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Рефераты, домашняя работа по математике скачать, учебники скатать бесплатно, онлайн уроки, вопросы и ответы
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|











