|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Пересечение прямой с окружностью</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Пересечение прямой с окружностью, пересечении, окружность, прямая, точек</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Пересечение прямой с окружностью''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Пересечение прямой с окружностью''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ОКРУЖНОСТЬЮ'''<br> | + | '''Пересечение прямой с окружностью'''<br> |
| | | | |
| - | <br>Рассмотрим вопрос о пересечении прямой с окружностью. | + | <br>Рассмотрим вопрос о [[Свойство углов, образованных при пересечении параллельных прямых секущей. Полные уроки|пересечении]] прямой с окружностью. |
| | | | |
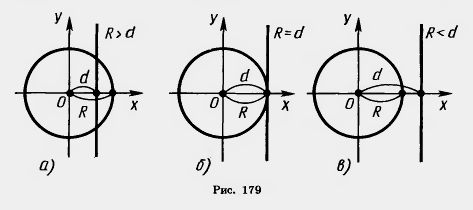
| - | Пусть R — радиус окружности и d — расстояние от центра окружности до прямой. Примем центр окружности за начало координат, а прямую, перпендикулярную к данной, за ось х (рис. 179). Тогда уравнением окружности будет x'<sup>2</sup> + y<sup>2</sup>=R<sup>2</sup>, а уравнением прямой x = d.<br> | + | Пусть R — радиус окружности и d — расстояние от центра окружности до прямой. Примем центр окружности за начало координат, а прямую, перпендикулярную к данной, за ось х (рис. 179). Тогда уравнением окружности будет x'<sup>2</sup> + y<sup>2</sup>=R<sup>2</sup>, а уравнением прямой x = d.<br> |
| | | | |
| - | Для того чтобы прямая и окружность пересекались, надо, чтобы система двух уравнений<br> | + | Для того чтобы прямая и [[Окружность|окружность]] пересекались, надо, чтобы система двух уравнений<br> |
| | | | |
| - | x'<sup>2</sup> + y<sup>2</sup>=R<sup>2</sup>, x = d<br> | + | x'<sup>2</sup> + y<sup>2</sup>=R<sup>2</sup>, x = d<br> |
| | | | |
| - | имела решение. И обратно: всякое решение этой системы дает координаты X, у точки пересечения прямой с окружностью. Решая нашу систему, получим:<br> | + | имела решение. И обратно: всякое решение этой системы дает координаты X, у точки пересечения прямой с окружностью. Решая нашу систему, получим:<br> |
| | | | |
| - | [[Image:22-06-118.jpg]]<br><br>[[Image:22-06-119.jpg]] <br> <br>Из выражения для у видно, что система имеет два решения, т. е. окружность и прямая имеют две точки пересечения, если R>d (рис. 179,а).<br> | + | [[Image:22-06-118.jpg|180px|Формула]]<br><br>[[Image:22-06-119.jpg|480px|Пересечение прямой с окружностью]] <br> <br>Из выражения для у видно, что система имеет два решения, т. е. окружность и [[Ілюстрації: Перетин прямих. Точка. відрізок. Порівняння відрізків за довжиною.|прямая]] имеют две точки пересечения, если R>d (рис. 179,а).<br> |
| | | | |
| - | Система имеет одно решение, если R=d (рис. 179,в).<br> | + | Система имеет одно решение, если R=d (рис. 179,в).<br> |
| | | | |
| - | В этом случае прямая и окружность касаются.<br> | + | В этом случае прямая и окружность касаются.<br> |
| | | | |
| - | Система не имеет решения, т. е. прямая и окружность не пересекаются, если R<.d (рис. 179, в).<br> | + | Система не имеет решения, т. е. прямая и окружность не пересекаются, если R<.d (рис. 179, в).<br> |
| | | | |
| - | Задача (50). Найдите точки пересечения окружности х^ + у' = 1 с прямой J/ = 2JC-1-1.<br>Решение. Так как точки пересечения лежат на окружности и на прямой, то их координаты удовлетворяют системе уравнений<br> | + | Задача (50). Найдите точки пересечения окружности х^ + у' = 1 с прямой J/ = 2JC-1-1.<br>Решение. Так как точки пересечения лежат на окружности и на прямой, то их координаты удовлетворяют системе уравнений<br> |
| | | | |
| - | х<sup>2</sup> + у<sup>2</sup> = 1, y = 2х+1.<br> | + | х<sup>2</sup> + у<sup>2</sup> = 1, y = 2х+1.<br> |
| | | | |
| - | Решим эту систему. Подставим у из второго уравнения в первое. Получим уравнение для х:<br> | + | Решим эту систему. Подставим у из второго уравнения в первое. Получим уравнение для х:<br> |
| | | | |
| - | 5x<sup>2</sup> + 4x = 0.<br> | + | 5x<sup>2</sup> + 4x = 0.<br> |
| | | | |
| - | Уравнение имеет два корня x<sub>1</sub> = 0 и[[Image:22-06-120.jpg]]. Это абсциссы точек пересечения. Ординаты этих точек получим из уравнения прямой, подставляя в него x<sub>1</sub> и x<sub>2</sub>. <br> | + | Уравнение имеет два корня x<sub>1</sub> = 0 и[[Image:22-06-120.jpg|Уравнение]]. Это абсциссы точек пересечения. Ординаты этих [[Точка, пряма, площина. Промінь. Відрізок. Презентація уроку|точек]] получим из уравнения прямой, подставляя в него x<sub>1</sub> и x<sub>2</sub>. <br> |
| | | | |
| - | Получаем | + | Получаем y<sub>1</sub> = l, [[Image:22-06-121.jpg|Уравнение]]Итак, точки пересечения прямой и окружности (0; 1) и [[Image:22-06-122.jpg|Точки]]. |
| | + | |
| | + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | y<sub>1</sub> = l, [[Image:22-06-121.jpg]]Итак, точки пересечения прямой и ок-ружности (0; 1) и [[Image:22-06-122.jpg]].<br><br><br><br>
| |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Сборник конспектов уроков по математике [[Математика|скачать]], календарно-тематическое планирование, учебники по всем предметам [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | | <sub>Сборник конспектов уроков по математике [[Математика|скачать]], календарно-тематическое планирование, учебники по всем предметам [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
| Строка 46: |
Строка 46: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Пусть R — радиус окружности и d — расстояние от центра окружности до прямой. Примем центр окружности за начало координат, а прямую, перпендикулярную к данной, за ось х (рис. 179). Тогда уравнением окружности будет x'2 + y2=R2, а уравнением прямой x = d.
имела решение. И обратно: всякое решение этой системы дает координаты X, у точки пересечения прямой с окружностью. Решая нашу систему, получим:
Система имеет одно решение, если R=d (рис. 179,в).
В этом случае прямая и окружность касаются.
Система не имеет решения, т. е. прямая и окружность не пересекаются, если R<.d (рис. 179, в).
Задача (50). Найдите точки пересечения окружности х^ + у' = 1 с прямой J/ = 2JC-1-1.
Решение. Так как точки пересечения лежат на окружности и на прямой, то их координаты удовлетворяют системе уравнений
Решим эту систему. Подставим у из второго уравнения в первое. Получим уравнение для х:
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.