|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Свойства движения</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Свойства движения, точки, прямой, треугольника, углы</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Свойства движения''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Свойства движения''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | '''СВОЙСТВА ДВИЖЕНИЯ'''
| + | '''Свойства движения''' |
| | | | |
| - | <br>Теорема 9.1. '''''Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.''''' | + | <br>'''Теорема 9.1. '''Точки, лежащие на прямой, при движении переходят в [[Точки і прямі, їх властивості. Закриті вправи|точки]], лежащие на прямой, и сохраняется порядок их взаимного расположения. |
| | | | |
| - | Это значит, что если точки А, В, С, лежащие на прямой, переходят в точки A<sub>1</sub>, В<sub>1</sub>, С<sub>1</sub>, то эти точки также лежат на прямой; если точка В лежит между точками А и С, то точка В<sub>1</sub> лежит между точками А<sub>1</sub> и C<sub>1</sub>. | + | Это значит, что если точки А, В, С, лежащие на прямой, переходят в точки A<sub>1</sub>, В<sub>1</sub>, С<sub>1</sub>, то эти точки также лежат на прямой; если точка В лежит между точками А и С, то точка В<sub>1</sub> лежит между точками А<sub>1</sub> и C<sub>1</sub>. |
| | | | |
| - | Доказательство. Пусть точка В прямой АС лежит между точками A и С. Докажем, что точки A<sub>1</sub>, В<sub>1</sub>, С<sub>1</sub> лежат на одной прямой. | + | Доказательство. Пусть точка В [[Плоскость. Прямая. Луч|прямой]] АС лежит между точками A и С. Докажем, что точки A<sub>1</sub>, В<sub>1</sub>, С<sub>1</sub> лежат на одной прямой. |
| | | | |
| - | Если точки A<sub>1</sub>, В<sub>1</sub>, С<sub>1</sub> не лежат на прямой, то они являются вершинами треугольника. Поэтому A<sub>1</sub>C<sub>1</sub> <A<sub>1</sub>B<sub>1</sub> + B<sub>1</sub>C<sub>1</sub>. По определению движения отсюда следует, что АС<АВ+ВС. Однако по свойству измерения отрезков АС = АВ + ВС. | + | Если точки A<sub>1</sub>, В<sub>1</sub>, С<sub>1</sub> не лежат на прямой, то они являются вершинами [[Задачі до теми Лічба в межах 20. Розв’язування задач на віднімання. Розпізнавання трикутників|треугольника]]. Поэтому A<sub>1</sub>C<sub>1</sub> <A<sub>1</sub>B<sub>1</sub> + B<sub>1</sub>C<sub>1</sub>. По определению движения отсюда следует, что АС<АВ+ВС. Однако по свойству измерения отрезков АС = АВ + ВС. |
| | | | |
| - | Мы пришли к противоречию. Значит, точка B<sub>1</sub> лежит на прямой А<sub>1</sub>С<sub>1</sub>. Первое утверждение теоремы доказано. | + | Мы пришли к противоречию. Значит, точка B<sub>1</sub> лежит на прямой А<sub>1</sub>С<sub>1</sub>. Первое утверждение теоремы доказано. |
| | | | |
| | Покажем теперь, что точка B<sub>1</sub> лежит между A<sub>1</sub> и C<sub>1</sub>. Допустим, что точка A<sub>1</sub> лежит между точками B<sub>1</sub> и C<sub>1</sub>. Тогда A<sub>1</sub>B<sub>1</sub> + А<sub>1</sub>С<sub>1</sub> =B<sub>1</sub>C<sub>1</sub> и, | | Покажем теперь, что точка B<sub>1</sub> лежит между A<sub>1</sub> и C<sub>1</sub>. Допустим, что точка A<sub>1</sub> лежит между точками B<sub>1</sub> и C<sub>1</sub>. Тогда A<sub>1</sub>B<sub>1</sub> + А<sub>1</sub>С<sub>1</sub> =B<sub>1</sub>C<sub>1</sub> и, |
| | | | |
| - | следовательно, АВ + AС=ВС. Но это противоречит равенству AВ + ВС=АС. Таким образом, точка A<sub>1</sub> не может лежать между точками B<sub>1</sub> и C<sub>1</sub>. | + | следовательно, АВ + AС=ВС. Но это противоречит равенству AВ + ВС=АС. Таким образом, точка A<sub>1</sub> не может лежать между точками B<sub>1</sub> и C<sub>1</sub>. |
| | | | |
| - | Аналогично доказывается, что точка C<sub>1</sub> не может лежать между точками A<sub>1</sub> и B<sub>1</sub>. | + | Аналогично доказывается, что точка C<sub>1</sub> не может лежать между точками A<sub>1</sub> и B<sub>1</sub>. |
| | | | |
| - | Так как из трех точек A<sub>1</sub>, В<sub>1</sub>, С<sub>1</sub>, одна лежит между двумя другими, то этой точкой может быть только B<sub>1</sub>. Теорема доказана полностью. | + | Так как из трех точек A<sub>1</sub>, В<sub>1</sub>, С<sub>1</sub>, одна лежит между двумя другими, то этой точкой может быть только B<sub>1</sub>. Теорема доказана полностью. |
| | | | |
| - | Из теоремы 9.1 следует, '''''что при движении прямые переходят в прямые, полупрямые — в полупрямые, отрезки — в отрезки''''' (рис. 185). | + | Из теоремы 9.1 следует, что при движении прямые переходят в прямые, полупрямые — в полупрямые, отрезки — в отрезки (рис. 185). |
| | | | |
| - | Докажем, что при движении сохраняются углы между полупрямыми.<br> <br>[[Image:22-06-137.jpg]] <br> | + | Докажем, что при движении сохраняются [[Построение угла, равного данному. Полные уроки|углы]] между полупрямыми.<br> <br>[[Image:22-06-137.jpg|480px|Свойства движения]] <br> |
| | | | |
| | + | <br> |
| | | | |
| | + | [[Image:22-06-138.jpg|480px|Свойства движения]]<br>Пусть АВ и АС — две полупрямые, исходящие из точки А, не лежащие на одной прямой (рис. 186). При движении эти полупрямые переходят в некоторые полупрямые A<sub>1</sub>, В<sub>1</sub>, и А<sub>1</sub>С<sub>1</sub>. Так как движение сохраняет расстояния, то треугольники ABC и A<sub>1</sub>, В<sub>1</sub>, С<sub>1</sub>, равны по третьему признаку равенства треугольников. Из равенства треугольников следует равенство углов ВАС и В<sub>1</sub>А<sub>1</sub>С<sub>1</sub>, что и требовалось доказать. <br> |
| | | | |
| - | [[Image:22-06-138.jpg]] | + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | <br>Пусть АВ и АС — две полупрямые, исходящие из точки А, не лежащие на одной прямой (рис. 186). При движении эти полупрямые переходят в некоторые полупрямые A<sub>1</sub>, В<sub>1</sub>, и А<sub>1</sub>С<sub>1</sub>. Так как движение сохраняет расстояния, то треугольники ABC и A<sub>1</sub>, В<sub>1</sub>, С<sub>1</sub>, равны по третьему признаку равенства треугольников. Из равенства треугольников следует равенство углов ВАС и В<sub>1</sub>А<sub>1</sub>С<sub>1</sub>, что и требовалось доказать. <br>
| |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Математика для 8 класса, учебники и книги по математике [[Математика|скачать]], библиотека [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> | | <sub>Математика для 8 класса, учебники и книги по математике [[Математика|скачать]], библиотека [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> |
| Строка 42: |
Строка 42: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 12:48, 9 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Свойства движения
Свойства движения
Теорема 9.1. Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.
Это значит, что если точки А, В, С, лежащие на прямой, переходят в точки A1, В1, С1, то эти точки также лежат на прямой; если точка В лежит между точками А и С, то точка В1 лежит между точками А1 и C1.
Доказательство. Пусть точка В прямой АС лежит между точками A и С. Докажем, что точки A1, В1, С1 лежат на одной прямой.
Если точки A1, В1, С1 не лежат на прямой, то они являются вершинами треугольника. Поэтому A1C1 <A1B1 + B1C1. По определению движения отсюда следует, что АС<АВ+ВС. Однако по свойству измерения отрезков АС = АВ + ВС.
Мы пришли к противоречию. Значит, точка B1 лежит на прямой А1С1. Первое утверждение теоремы доказано.
Покажем теперь, что точка B1 лежит между A1 и C1. Допустим, что точка A1 лежит между точками B1 и C1. Тогда A1B1 + А1С1 =B1C1 и,
следовательно, АВ + AС=ВС. Но это противоречит равенству AВ + ВС=АС. Таким образом, точка A1 не может лежать между точками B1 и C1.
Аналогично доказывается, что точка C1 не может лежать между точками A1 и B1.
Так как из трех точек A1, В1, С1, одна лежит между двумя другими, то этой точкой может быть только B1. Теорема доказана полностью.
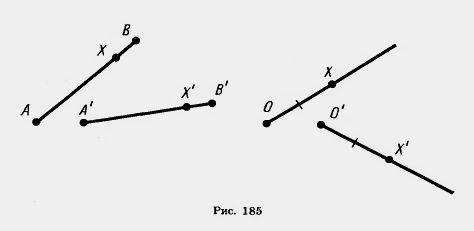
Из теоремы 9.1 следует, что при движении прямые переходят в прямые, полупрямые — в полупрямые, отрезки — в отрезки (рис. 185).
Докажем, что при движении сохраняются углы между полупрямыми.
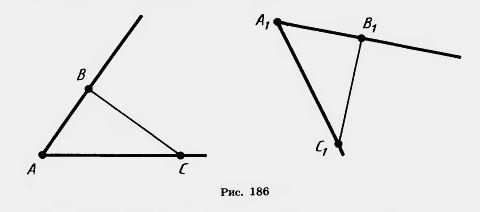
Пусть АВ и АС — две полупрямые, исходящие из точки А, не лежащие на одной прямой (рис. 186). При движении эти полупрямые переходят в некоторые полупрямые A1, В1, и А1С1. Так как движение сохраняет расстояния, то треугольники ABC и A1, В1, С1, равны по третьему признаку равенства треугольников. Из равенства треугольников следует равенство углов ВАС и В1А1С1, что и требовалось доказать.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Математика для 8 класса, учебники и книги по математике скачать, библиотека онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|












