|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Геометрия, урок, на Тему, Построение некоторых правильных многоугольников</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Геометрия, урок, на Тему, Построение некоторых правильных многоугольников, правильного многоугольника, окружности, четырехугольника, многоугольника</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Построение некоторых правильных многоугольников''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Построение некоторых правильных многоугольников''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' ПОСТРОЕНИЕ НЕКОТОРЫХ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ''' | + | '''Построение некоторых правильных многоугольников''' |
| | | | |
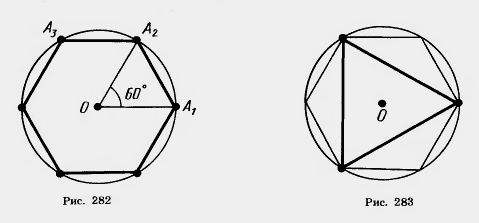
| - | <br>Для построения правильного многоугольника, вписанного в окружность, достаточно построить его центральный угол.<br>У правильного шестиугольника такой угол равен [[Image:24-06-83.jpg]]<br>Поэтому для построения правильного шестиугольника одну вершину (A<sub>1</sub>) на окружности берем произвольно. Из нее как из центра радиусом, равным радиусу окружности, делаем засечку и получаем вершину Аг (рис. 282). Затем аналогично строим остальные вершины А<sub>3</sub>, А<sub>4</sub>, А<sub>5</sub>, A<sub>6</sub> и соединяем их отрезками. | + | <br>Для построения [[Правильные многоугольники|правильного многоугольника]], вписанного в окружность, достаточно построить его центральный угол. |
| | | | |
| - | Для построения правильного вписанного треугольника достаточно соединить через одну вершины правильного вписанного шестиугольника (рис. 283).
| + | У правильного шестиугольника такой угол равен [[Image:24-06-83.jpg|Формула]] |
| | | | |
| | + | Поэтому для построения правильного шестиугольника одну вершину (A<sub>1</sub>) на окружности берем произвольно. Из нее как из центра радиусом, равным радиусу [[Окружность, описанная около треугольника. Полные уроки|окружности]], делаем засечку и получаем вершину Аг (рис. 282). Затем аналогично строим остальные вершины А<sub>3</sub>, А<sub>4</sub>, А<sub>5</sub>, A<sub>6</sub> и соединяем их отрезками. |
| | | | |
| | + | Для построения правильного вписанного треугольника достаточно соединить через одну вершины правильного вписанного шестиугольника (рис. 283). |
| | | | |
| - | [[Image:24-06-84.jpg]]<br> <br>Для построения правильного вписанного четырехугольника (квадрата) достаточно провести через центр окружности перпендикулярные прямые. Они пересекут окружность в вершинах квадрата (рис. 284).
| + | <br> |
| | | | |
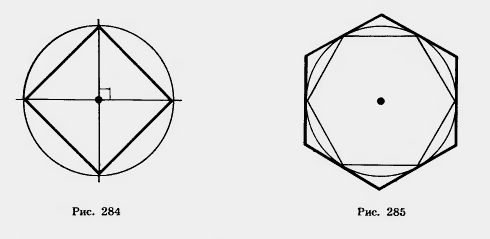
| | + | [[Image:24-06-84.jpg|480px|Построение некоторых правильных многоугольников]]<br> <br>Для построения правильного вписанного [[Чотирикутник i його елементи|четырехугольника]] (квадрата) достаточно провести через центр окружности перпендикулярные прямые. Они пересекут окружность в вершинах квадрата (рис. 284). |
| | | | |
| | + | <br> |
| | | | |
| - | [[Image:24-06-85.jpg]]<br> <br>Для построения правильного описанного многоугольника достаточно провести касательные к окружности в вершинах правильного вписанного многоугольника. Касательные, проходящие через вершины правильного вписанного многоугольника, пересекаются в вершинах правильного описанного многоугольника (рис. 285). | + | [[Image:24-06-85.jpg|480px|Построение некоторых правильных многоугольников]]<br> <br>Для построения правильного описанного многоугольника достаточно провести касательные к окружности в вершинах правильного вписанного многоугольника. Касательные, проходящие через вершины правильного вписанного многоугольника, пересекаются в вершинах правильного описанного [[Площадь ортогональной проекции многоугольника|многоугольника]] (рис. 285). |
| | | | |
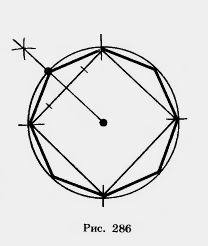
| - | Если в окружность вписан правильный n-угольник, то легко построить правильный вписанный 2n-угольник. На рисунке 286 показано построение правильного восьмиугольника. | + | Если в окружность вписан правильный n-угольник, то легко построить правильный вписанный 2n-угольник. На рисунке 286 показано построение правильного восьмиугольника.<br> |
| | | | |
| | + | [[Image:24-06-86.jpg|180px|Восьмиугольник]] |
| | | | |
| | + | <br> ''А. В. Погорелов,[http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | [[Image:24-06-86.jpg]]<br>
| |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Учебники по всему предметам [[Математика|скачать]], разработка планов уроков для учителей, Математика для 9 класса [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | | <sub>Учебники по всему предметам [[Математика|скачать]], разработка планов уроков для учителей, Математика для 9 класса [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
| Строка 32: |
Строка 36: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Для построения правильного вписанного треугольника достаточно соединить через одну вершины правильного вписанного шестиугольника (рис. 283).
Если в окружность вписан правильный n-угольник, то легко построить правильный вписанный 2n-угольник. На рисунке 286 показано построение правильного восьмиугольника.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.