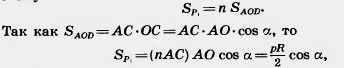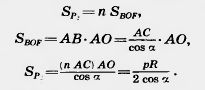|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Геометрия, урок, на Тему, Площадь круга</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, Геометрия, урок, на Тему, Площадь круга, площадь, фигуры, плоскости, круг, многоугольник</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Площадь круга''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Площадь круга''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' ПЛОЩАДЬ КРУГА''' | + | '''Площадь круга''' |
| | | | |
| - | <br>'''''Если фигура простая, т. е. допускает разбиение на конечное число треугольников, то ее площадь равна сумме площадей этих треугольников.''''' Для произвольной фигуры площадь определяется следующим образом. | + | <br>Если фигура простая, т. е. допускает разбиение на конечное число треугольников, то ее [[Понятие площади|площадь]] равна сумме площадей этих треугольников. Для произвольной фигуры площадь определяется следующим образом. |
| | | | |
| - | Данная фигура имеет площадь S, если существуют содержащие ее простые фигуры и содержащиеся в ней простые фигуры с площадями, как угодно мало отличающимися от S. Применим это определение к нахождению площади круга. | + | Данная фигура имеет площадь S, если существуют содержащие ее простые фигуры и содержащиеся в ней простые [[Геометрические фигуры|фигуры]] с площадями, как угодно мало отличающимися от S. Применим это определение к нахождению площади круга. |
| | | | |
| - | [[Image:29-06-52.jpg]] | + | [[Image:29-06-52.jpg|480px|Площадь круга]] |
| | | | |
| - | '''''Кругом называется фигура, состоящая из всех точек плоскости, расстояние от которых до данной точки не больше данного.''''' Эта точка называется '''''центром круга''''', а данное расстояние — '''''радиусом круга'''''. Границей круга является окружность с теми же центром и радиусом (рис. 304).
| + | Кругом называется фигура, состоящая из всех точек [[Розв’язування задач на перпендикулярність прямої та площини|плоскости]], расстояние от которых до данной точки не больше данного. Эта точка называется центром круга, а данное расстояние — радиусом круга. Границей круга является окружность с теми же центром и радиусом (рис. 304). |
| | | | |
| - | '''''Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.'''''
| + | Площадь круга равна половине произведения длины ограничивающей его окружности на радиус. |
| | | | |
| - | Докажем это. Построим два правильных п-угольника: Р<sub>1</sub> — вписанный в круг и Р<sub>2</sub> — описанный около круга (рис. 305). Многоугольники Р<sub>1</sub> и Р<sub>2</sub> являются простыми фигурами. Многоугольник Р<sub>2</sub> содержит круг, а многоугольник Р<sub>1</sub> содержится в круге. | + | Докажем это. Построим два правильных n-угольника: Р<sub>1</sub> — вписанный в круг и Р<sub>2</sub> — описанный около круга (рис. 305). Многоугольники Р<sub>1</sub> и Р<sub>2</sub> являются простыми фигурами. Многоугольник Р<sub>2</sub> содержит круг, а многоугольник Р<sub>1</sub> содержится в круге. |
| | | | |
| - | Радиусы, проведенные в вершины многоугольника Р<sub>1</sub>, разбивают его на n треугольников, равных треугольнику AOD. Поэтому | + | Радиусы, проведенные в вершины многоугольника Р<sub>1</sub>, разбивают его на n треугольников, равных треугольнику AOD. Поэтому |
| | | | |
| - | [[Image:29-06-53.jpg]]<br><br>где р — периметр многоугольника Р<sub>1</sub>, R — радиус круга. Аналогично находим площадь многоугольника Р<sub>2</sub>: | + | [[Image:29-06-53.jpg|32[[Коло, круг, їх елементи|круг]]0px|Площадь круга]]<br><br>где р — периметр многоугольника Р<sub>1</sub>, R — радиус круга. Аналогично находим площадь многоугольника Р<sub>2</sub>: |
| | | | |
| - | [[Image:29-06-54.jpg]]<br> <br>Итак, многоугольник P<sub>1</sub>, содержащийся в круге, имеет площадь | + | [[Image:29-06-54.jpg|240px|Площадь круга]]<br> <br>Итак, многоугольник P<sub>1</sub>, содержащийся в круге, имеет площадь |
| | | | |
| - | [[Image:29-06-55.jpg]]<br> <br>а многоугольник Р<sub>2</sub>, содержащий круг, имеет площадь | + | [[Image:29-06-55.jpg|120px|Площадь]]<br> <br>а [[Правильные многоугольники|многоугольник]] Р<sub>2</sub>, содержащий круг, имеет площадь |
| | | | |
| - | [[Image:29-06-56.jpg]]<br><br>Так как при достаточно большом n периметр р отличается сколь угодно мало от длины l окружности, а cos [[Image:24-06-52.jpg]] сколь угодно мало отличается от единицы, то площади многоугольников<br>Р<sub>1</sub> и P<sub>2</sub> сколь угодно мало отличаются от [[Image:29-06-57.jpg]]. Согласно определению это значит, что площадь круга | + | [[Image:29-06-56.jpg|120px|Площадь]]<br><br>Так как при достаточно большом n периметр р отличается сколь угодно мало от длины l окружности, а cos [[Image:24-06-52.jpg]] сколь угодно мало отличается от единицы, то площади многоугольников Р<sub>1</sub> и P<sub>2</sub> сколь угодно мало отличаются от [[Image:29-06-57.jpg]]. Согласно определению это значит, что площадь круга |
| | | | |
| - | [[Image:29-06-58.jpg]] | + | [[Image:29-06-58.jpg|120px|Площадь]] |
| | | | |
| - | что и требовалось доказать. | + | что и требовалось доказать. |
| | | | |
| - | '''''Круговым сектором называется часть круга, лежащая внутри соответствующего центрального угла''''' (рис. 306).<br>Площадь кругового сектора вычисляется по формуле<br>
| + | Круговым сектором называется часть круга, лежащая внутри соответствующего центрального угла (рис. 306). |
| | | | |
| - | [[Image:29-06-59.jpg]]<br><br>где R — радиус круга, а [[Image:24-06-52.jpg]] — градусная мера соответствующего центрального угла.
| + | Площадь кругового сектора вычисляется по формуле<br> |
| | | | |
| - | '''''Круговым сегментом называется общая часть круга и полуплоскости ('''''рис. 307).
| + | [[Image:29-06-59.jpg|80px|Формула]]<br>где R — радиус круга, а [[Image:24-06-52.jpg]] — градусная мера соответствующего центрального угла. |
| | | | |
| - | Площадь сегмента, не равного полукругу, вычисляется по формуле
| + | Круговым сегментом называется общая часть круга и полуплоскости (рис. 307). |
| | | | |
| - | [[Image:29-06-60.jpg]]<br><br>где [[Image:24-06-52.jpg]] — градусная мера центрального угла, который содержит дугу этого кругового сегмента, а S, — площадь треугольника с вершинами в центре круга и концах радиусов, ограничивающих соответствующий сектор. Знак « — » надо брать, когда [[Image:24-06-52.jpg]]< 180°, а знак «+» надо брать, когда [[Image:24-06-52.jpg]]> 180°.<br> <br>[[Image:29-06-61.jpg]] | + | Площадь сегмента, не равного полукругу, вычисляется по формуле |
| | + | |
| | + | [[Image:29-06-60.jpg|120px|Формула]]<br><br>где [[Image:24-06-52.jpg]] — градусная мера центрального угла, который содержит дугу этого кругового сегмента, а S, — площадь треугольника с вершинами в центре круга и концах радиусов, ограничивающих соответствующий сектор. Знак « — » надо брать, когда [[Image:24-06-52.jpg]]< 180°, а знак «+» надо брать, когда [[Image:24-06-52.jpg]]> 180°.<br> <br>[[Image:29-06-61.jpg|480px|Части круга]] |
| | + | |
| | + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - |
| |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Библиотека с учебниками и книгами на скачку бесплатно [[Гипермаркет знаний - первый в мире!|онлайн]], Математика для 9 класса [[Математика|скачать]], школьная программа по математике, планы конспектов уроков </sub> | | <sub>Библиотека с учебниками и книгами на скачку бесплатно [[Гипермаркет знаний - первый в мире!|онлайн]], Математика для 9 класса [[Математика|скачать]], школьная программа по математике, планы конспектов уроков </sub> |
| Строка 52: |
Строка 54: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 13:14, 11 октября 2012
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика:Площадь круга
Площадь круга
Если фигура простая, т. е. допускает разбиение на конечное число треугольников, то ее площадь равна сумме площадей этих треугольников. Для произвольной фигуры площадь определяется следующим образом.
Данная фигура имеет площадь S, если существуют содержащие ее простые фигуры и содержащиеся в ней простые фигуры с площадями, как угодно мало отличающимися от S. Применим это определение к нахождению площади круга.
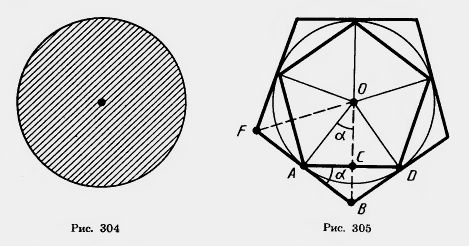
Кругом называется фигура, состоящая из всех точек плоскости, расстояние от которых до данной точки не больше данного. Эта точка называется центром круга, а данное расстояние — радиусом круга. Границей круга является окружность с теми же центром и радиусом (рис. 304).
Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.
Докажем это. Построим два правильных n-угольника: Р1 — вписанный в круг и Р2 — описанный около круга (рис. 305). Многоугольники Р1 и Р2 являются простыми фигурами. Многоугольник Р2 содержит круг, а многоугольник Р1 содержится в круге.
Радиусы, проведенные в вершины многоугольника Р1, разбивают его на n треугольников, равных треугольнику AOD. Поэтому
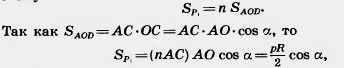
где р — периметр многоугольника Р1, R — радиус круга. Аналогично находим площадь многоугольника Р2:
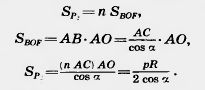
Итак, многоугольник P1, содержащийся в круге, имеет площадь
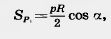
а многоугольник Р2, содержащий круг, имеет площадь
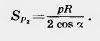
Так как при достаточно большом n периметр р отличается сколь угодно мало от длины l окружности, а cos  сколь угодно мало отличается от единицы, то площади многоугольников Р1 и P2 сколь угодно мало отличаются от сколь угодно мало отличается от единицы, то площади многоугольников Р1 и P2 сколь угодно мало отличаются от 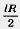 . Согласно определению это значит, что площадь круга . Согласно определению это значит, что площадь круга
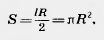
что и требовалось доказать.
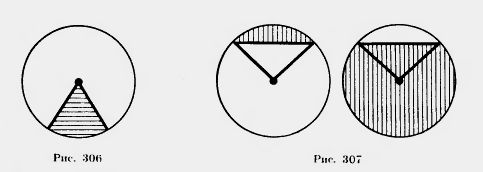
Круговым сектором называется часть круга, лежащая внутри соответствующего центрального угла (рис. 306).
Площадь кругового сектора вычисляется по формуле
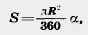
где R — радиус круга, а  — градусная мера соответствующего центрального угла. — градусная мера соответствующего центрального угла.
Круговым сегментом называется общая часть круга и полуплоскости (рис. 307).
Площадь сегмента, не равного полукругу, вычисляется по формуле
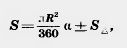
где  — градусная мера центрального угла, который содержит дугу этого кругового сегмента, а S, — площадь треугольника с вершинами в центре круга и концах радиусов, ограничивающих соответствующий сектор. Знак « — » надо брать, когда — градусная мера центрального угла, который содержит дугу этого кругового сегмента, а S, — площадь треугольника с вершинами в центре круга и концах радиусов, ограничивающих соответствующий сектор. Знак « — » надо брать, когда  < 180°, а знак «+» надо брать, когда < 180°, а знак «+» надо брать, когда  > 180°. > 180°.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Библиотека с учебниками и книгами на скачку бесплатно онлайн, Математика для 9 класса скачать, школьная программа по математике, планы конспектов уроков
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|