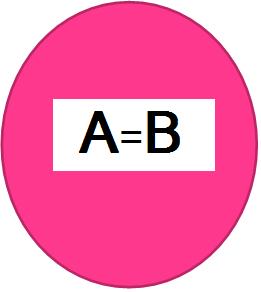|
|
|
| Строка 1: |
Строка 1: |
| - | Презентация урока к предмету [[Информатика|Информатика]], [[Информатика_6_класс|6 класс]] | + | Презентация урока к предмету [[Информатика|Информатика]], [[Информатика 6 класс|6 класс]] |
| | | | |
| - | '''''Тема: «'''''[[Отношения_между_понятиями|'''''Отношения между понятиями''''']]'''''»''''' | + | '''''Тема: «'''''[[Отношения между понятиями|'''''Отношения между понятиями''''']]'''''»''''' |
| | | | |
| - | <br> Сравнимые понятия – это те, у которых есть <br>общее, объединяющее их так называемое <br>родовое понятие (например, клен, тополь ель – <br>дерево, растение). <br>У несравнимых понятий такого родового <br>понятия нет (например, студент (человек) и <br>студенческий билет – (документ)).<br><br>Рассмотрим два понятия: квадрат и прямоугольник<br> | + | <br> Сравнимые понятия – это те, у которых есть <br>общее, объединяющее их так называемое <br>родовое понятие (например, клен, тополь ель – <br>дерево, растение). <br>У несравнимых понятий такого родового <br>понятия нет (например, студент (человек) и <br>студенческий билет – (документ)).<br><br>Рассмотрим два понятия: квадрат и прямоугольник<br> |
| | | | |
| - | {| width="313" height="205" cellspacing="1" cellpadding="1" border="1" | + | {| width="313" cellspacing="1" cellpadding="1" border="1" |
| | |- | | |- |
| - | | Квадрат <br> | + | | Квадрат <br> |
| | | | | | |
| - | • Четырехугольник;� <br> | + | • Четырехугольник;<br> |
| | | | |
| - | • Все углы прямые;� <br> | + | • Все углы прямые; <br> |
| | | | |
| - | • Все стороны равны | + | • Все стороны равны |
| | | | |
| | |- | | |- |
| - | | Прямоугольник | + | | Прямоугольник |
| | | | | | |
| - | • Четырехугольник; | + | • Четырехугольник; |
| | | | |
| - | • Все углы прямые; | + | • Все углы прямые; |
| | | | |
| - | • Длины противоположных сторон попарно равны | + | • Длины противоположных сторон попарно равны |
| | | | |
| | |} | | |} |
| | | | |
| - | <br>Как видно, содержания понятий отличаются одним признаком: у квадрата длины всех сторон равны, а у прямоугольника длины противоположных сторон попарно равны.<br><br>Объем понятия «прямоугольник» больше объема понятия «квадрат», так как все квадраты — тоже прямоугольники. | + | <br>Как видно, содержания понятий отличаются одним признаком: у квадрата длины всех сторон равны, а у прямоугольника длины противоположных сторон попарно равны.<br><br>Объем понятия «прямоугольник» больше объема понятия «квадрат», так как все квадраты — тоже прямоугольники. |
| | | | |
| | Сравнимые понятия по объему бывают в отношениях совместимости и несовместимости. В отношениях совместимости – те понятия, объемы которых хотя бы частично совпадают, имеется общий элемент (например, юрист, адвокат – часть юристов – адвокаты). | | Сравнимые понятия по объему бывают в отношениях совместимости и несовместимости. В отношениях совместимости – те понятия, объемы которых хотя бы частично совпадают, имеется общий элемент (например, юрист, адвокат – часть юристов – адвокаты). |
| | | | |
| - | <br>В отношениях несовместимости – те понятия, объемы которых нисколько не совпадают (например, адвокат, прокурор, судья – адвокат не может подрабатывать судьей).<br><br><u>'''Рассмотрим некоторые соотношения между сравнимыми понятиями'''</u> | + | <br>В отношениях несовместимости – те понятия, объемы которых нисколько не совпадают (например, адвокат, прокурор, судья – адвокат не может подрабатывать судьей).<br><br><u>'''Рассмотрим некоторые соотношения между сравнимыми понятиями'''</u> |
| | | | |
| - | <br>'''Отношение «тождество»'''<br>Если объемы понятий совпадают, другими словами, объем одного понятия равен объему другого, то отношение между этими понятиями называют тождеством. Например, понятия «столица России» (А) и «город Москва» <br>(В) — это тождественные понятия. Графическое представление отношения между ними будет выглядеть так: | + | <br>'''Отношение «тождество»'''<br>Если объемы понятий совпадают, другими словами, объем одного понятия равен объему другого, то отношение между этими понятиями называют тождеством. Например, понятия «столица России» (А) и «город Москва» <br>(В) — это тождественные понятия. Графическое представление отношения между ними будет выглядеть так: |
| | | | |
| - | [[Image:1_opcii_okt2012-ch24.jpg|300px]] | + | [[Image:1 opcii okt2012-ch24.jpg|300px]] |
| | | | |
| | + | <br> |
| | | | |
| | + | '''Отношение "пересечение"'''<br>Пересечением называют отношение между понятиями, объемы которых совпадают частично, то есть содержат общие элементы. Пусть понятие А — «электронное письмо», В — «письмо на русском языке». Тогда: |
| | | | |
| - | '''Отношение "пересечение"'''<br>Пересечением называют отношение между понятиями, объемы которых совпадают частично, то есть содержат общие элементы. Пусть понятие А — «электронное письмо», В — «письмо на русском языке». Тогда:
| + | [[Image:1 opcii okt2012-ch25.jpg|300px]] |
| | | | |
| - | [[Image:1_opcii_okt2012-ch25.jpg|300px]]
| + | <br> |
| | | | |
| - | | + | '''Отношение "подчинение"'''<br>Подчинением называют отношение между понятиями когда объем одного из них полностью входит в объем другого понятия, но не исчерпывает его. Пусть понятие А — клавиатура, понятие В — «устройство ввода».<br><br> |
| - | | + | |
| - | '''Отношение "подчинение"'''<br>Подчинением называют отношение между понятиями когда объем одного из них полностью входит в объем другого понятия, но не исчерпывает его. Пусть понятие А — клавиатура, понятие В — «устройство ввода».<br><br> | + | |
| | | | |
| | Скачать полную презентацию урока можно нажав на текст [http://school.xvatit.com/Presentation/Gipermarket_october_2012/Informatiki_Pastuh_okt2012/Chebaniuk/Rus/6kl_Т2.3.3_inf_3prez.ppt Скачать презентацию урока] и установив Microsoft PowerPoint | | Скачать полную презентацию урока можно нажав на текст [http://school.xvatit.com/Presentation/Gipermarket_october_2012/Informatiki_Pastuh_okt2012/Chebaniuk/Rus/6kl_Т2.3.3_inf_3prez.ppt Скачать презентацию урока] и установив Microsoft PowerPoint |
| | | | |
| - | '''''<br> Прислано учителем-участником Гильдии Лидеров образования Чебанюк''''' | + | '''''<br> Прислано учителем-участником Гильдии Лидеров образования Чебанюк''''' |
| | | | |
| | [[Category:Отношения_между_понятиями._Презентация_урока]] | | [[Category:Отношения_между_понятиями._Презентация_урока]] |
Текущая версия на 11:51, 16 октября 2012
Презентация урока к предмету Информатика, 6 класс
Тема: «Отношения между понятиями»
Сравнимые понятия – это те, у которых есть
общее, объединяющее их так называемое
родовое понятие (например, клен, тополь ель –
дерево, растение).
У несравнимых понятий такого родового
понятия нет (например, студент (человек) и
студенческий билет – (документ)).
Рассмотрим два понятия: квадрат и прямоугольник
Квадрат
|
• Четырехугольник;
• Все углы прямые;
• Все стороны равны
|
| Прямоугольник
|
• Четырехугольник;
• Все углы прямые;
• Длины противоположных сторон попарно равны
|
Как видно, содержания понятий отличаются одним признаком: у квадрата длины всех сторон равны, а у прямоугольника длины противоположных сторон попарно равны.
Объем понятия «прямоугольник» больше объема понятия «квадрат», так как все квадраты — тоже прямоугольники.
Сравнимые понятия по объему бывают в отношениях совместимости и несовместимости. В отношениях совместимости – те понятия, объемы которых хотя бы частично совпадают, имеется общий элемент (например, юрист, адвокат – часть юристов – адвокаты).
В отношениях несовместимости – те понятия, объемы которых нисколько не совпадают (например, адвокат, прокурор, судья – адвокат не может подрабатывать судьей).
Рассмотрим некоторые соотношения между сравнимыми понятиями
Отношение «тождество»
Если объемы понятий совпадают, другими словами, объем одного понятия равен объему другого, то отношение между этими понятиями называют тождеством. Например, понятия «столица России» (А) и «город Москва»
(В) — это тождественные понятия. Графическое представление отношения между ними будет выглядеть так:
Отношение "пересечение"
Пересечением называют отношение между понятиями, объемы которых совпадают частично, то есть содержат общие элементы. Пусть понятие А — «электронное письмо», В — «письмо на русском языке». Тогда:
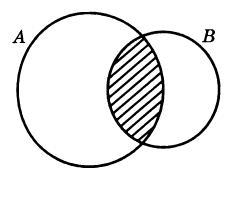
Отношение "подчинение"
Подчинением называют отношение между понятиями когда объем одного из них полностью входит в объем другого понятия, но не исчерпывает его. Пусть понятие А — клавиатура, понятие В — «устройство ввода».
Скачать полную презентацию урока можно нажав на текст Скачать презентацию урока и установив Microsoft PowerPoint
Прислано учителем-участником Гильдии Лидеров образования Чебанюк
Предмети > Информатика > Информатика 6 класс > Отношения между понятиями > Отношения между понятиями. Презентация урока
|