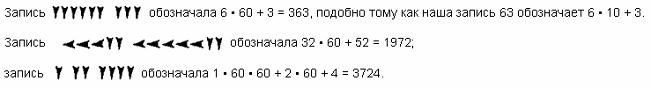|
|
| Строка 1: |
Строка 1: |
| - | Презентация урока к предмету [[Информатика|Информатика]], [[Информатика_6_класс|6 класс]] | + | Презентация урока к предмету [[Информатика|Информатика]], [[Информатика 6 класс|6 класс]] |
| | | | |
| - | '''''Тема: «'''''[[Вавилонская_система_счисления|'''''Вавилонская система счисления''''']]'''''»''''' | + | '''''Тема: «'''''[[Вавилонская система счисления|'''''Вавилонская система счисления''''']]'''''»''''' |
| | | | |
| - | <br> Шестидесятеричная вавилонская система - первая известная нам система счисления, основанная на позиционном принципе. <br><br>Идея приписывать цифрам разные величины взависимости от того, какую позицию они занимают в записи числа, впервые появилась в III тысячелетии до н.э. в Месопотамии (Междуречье) у шумеров. От них она перешла к вавилонянам - новым хозяевам Междуречья, почему и вошла в историю как вавилонская система счисления. <br> | + | <br> Шестидесятеричная вавилонская система - первая известная нам система счисления, основанная на позиционном принципе. <br><br>Идея приписывать цифрам разные величины взависимости от того, какую позицию они занимают в записи числа, впервые появилась в III тысячелетии до н.э. в Месопотамии (Междуречье) у шумеров. От них она перешла к вавилонянам - новым хозяевам Междуречья, почему и вошла в историю как вавилонская система счисления. <br> |
| | | | |
| - | Все число в целом записывалось в позиционной системе счисления с основанием 60. Поясним это на примерах.<br> | + | Все число в целом записывалось в позиционной системе счисления с основанием 60. Поясним это на примерах.<br> |
| | | | |
| - | [[Image:1_opcii_okt2012-ch39.jpg|500px]] | + | [[Image:1 opcii okt2012-ch39.jpg|500px|1 opcii okt2012-ch39.jpg]] |
| | | | |
| | + | <br> |
| | | | |
| | + | Для определения значения числа надо было изображение числа разбить на разряды справа налево. Чередование групп одинаковых знаков ("цифр") соответствовало чередованию разрядов:<br>= 2 х 60 + 12 = 132<br> |
| | | | |
| - | Для определения значения числа надо было изображение числа разбить на разряды справа налево. Чередование групп одинаковых знаков ("цифр") соответствовало чередованию разрядов:<br>= 2 х 60 + 12 = 132<br>
| + | Шестидесятеричная система широко применялась в астрономических расчетах вплоть до эпохи возрождения. Именно ею пользовался во II веке н.э. греческий математик и астроном Клавдий Птолемей при составлении таблицы синусов (древнейшей из дошедших до нас).<br>[[Image:1 opcii okt2012-ch40.jpg|300px|1 opcii okt2012-ch40.jpg]] |
| | | | |
| - | Шестидесятеричная система широко применялась в астрономических расчетах вплоть до эпохи возрождения. Именно ею пользовался во II веке н.э. греческий математик и астроном Клавдий Птолемей при составлении таблицы синусов (древнейшей из дошедших до нас).<br>[[Image:1_opcii_okt2012-ch40.jpg|500px]]
| + | <br> |
| - | | + | |
| - | | + | |
| - | | + | |
| - | Отголоски этой системы счисления мы находим в сохранившемся до наших дней обыкновении делить один час на 60 минут, одну минуту на 60 секунд, полный угол — на 360 градусов.<br>[[Image:1_opcii_okt2012-ch41.jpg|500px]]
| + | |
| | | | |
| | + | Отголоски этой системы счисления мы находим в сохранившемся до наших дней обыкновении делить один час на 60 минут, одну минуту на 60 секунд, полный угол — на 360 градусов.<br>[[Image:1 opcii okt2012-ch41.jpg|300px|1 opcii okt2012-ch41.jpg]] |
| | | | |
| | + | <br> |
| | | | |
| | Скачать полную презентацию урока можно нажав на текст [http://school.xvatit.com/Presentation/Gipermarket_october_2012/Informatiki_Pastuh_okt2012/Chebaniuk/Rus/6kl_Т4.8_inf_3prez.ppt Скачать презентацию урока] и установив Microsoft PowerPoint | | Скачать полную презентацию урока можно нажав на текст [http://school.xvatit.com/Presentation/Gipermarket_october_2012/Informatiki_Pastuh_okt2012/Chebaniuk/Rus/6kl_Т4.8_inf_3prez.ppt Скачать презентацию урока] и установив Microsoft PowerPoint |
| | | | |
| - | '''''<br> Прислано учителем-участником Гильдии Лидеров образования Чебанюк''''' | + | '''''<br> Прислано учителем-участником Гильдии Лидеров образования Чебанюк''''' |
| | | | |
| | [[Category:Вавилонская_система_счисления._Презентация_урока]] | | [[Category:Вавилонская_система_счисления._Презентация_урока]] |
Все число в целом записывалось в позиционной системе счисления с основанием 60. Поясним это на примерах.
Для определения значения числа надо было изображение числа разбить на разряды справа налево. Чередование групп одинаковых знаков ("цифр") соответствовало чередованию разрядов:
= 2 х 60 + 12 = 132
Шестидесятеричная система широко применялась в астрономических расчетах вплоть до эпохи возрождения. Именно ею пользовался во II веке н.э. греческий математик и астроном Клавдий Птолемей при составлении таблицы синусов (древнейшей из дошедших до нас).

Отголоски этой системы счисления мы находим в сохранившемся до наших дней обыкновении делить один час на 60 минут, одну минуту на 60 секунд, полный угол — на 360 градусов.