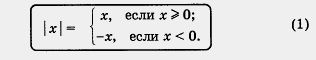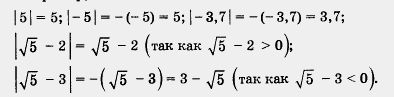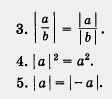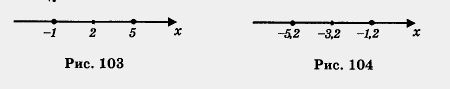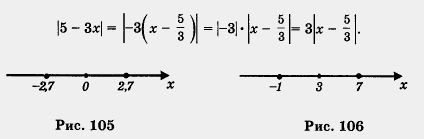|
|
|
| Строка 55: |
Строка 55: |
| | [[Image:14-06-139.jpg]]<br><br>4. Тождество [[Image:14-06-140.jpg]]<br>Мы знаем, что если [[Image:14-06-141.jpg]].А как быть, если а < 0? Написать у [[Image:14-06-142.jpg]] в этом случае нельзя, ведь а < 0 и получится, что [[Image:14-06-143.jpg]], а это неверно, так как значение квадратного корня не может быть отрицательным. | | [[Image:14-06-139.jpg]]<br><br>4. Тождество [[Image:14-06-140.jpg]]<br>Мы знаем, что если [[Image:14-06-141.jpg]].А как быть, если а < 0? Написать у [[Image:14-06-142.jpg]] в этом случае нельзя, ведь а < 0 и получится, что [[Image:14-06-143.jpg]], а это неверно, так как значение квадратного корня не может быть отрицательным. |
| | | | |
| - | Чему же равно выражение[[Image:14-06-144.jpg]] при а < 0? По определению квадратного корня в ответе должно получиться такое число, которое, во-первых, положительно и, во-вторых, при возведении в квадрат дает подкоренное число, т. е. а<sup>2</sup>. Таким числом будет - а. Смотрите: | + | Чему же равно выражение[[Image:14-06-144.jpg]] при а < 0? По определению квадратного корня в ответе должно получиться такое число, которое, во-первых, положительно и, во-вторых, при возведении в квадрат дает подкоренное число, т. е. а<sup>2</sup>. Таким числом будет - а. Смотрите:<br>1) - а > 0 (еще раз напомним, что а — отрицательное число, значит, - а — положительное число); <br>2)(-а)<sup>2</sup>=а<sup>2</sup>. <br>Итак, |
| | | | |
| - | <br>1) - а > 0 (еще раз напомним, что а — отрицательное число, <br>значит, - а — положительное число); <br>2)(-аJ=а2. <br>Итак, <br>Г а, если а > 0; <br>[-а, если а < 0. <br>Вам ничего не напоминает конструкция, полученная в пра- <br>вой части равенства? Вспомните, ведь точно так же определяет- <br>ся модуль числа а: <br>а, если а > 0; <br>[-а, еслиа<0. <br>а2 = <br>а = <br>I—2 <br>Значит, у а и | а \ — одно и то же. Тем самым <br>мы доказали важное тождество: <br>а <br>В роли а может выступать любое числовое или алгебраиче- <br>ское выражение. <br>Пример 4. Упростить выражение ^/(а-1J , если: <br>а) а - 1 > 0; б) а - 1 < 0. <br>Решение. Как мы только что установили, справедливо <br>тождество <br>а) Если а - 1 > 0, то | а - 11 = а - 1. Таким образом, в этом <br>случае получаем ^/(а-1J = а - 1. <br>б) Если а - 1 <0, то|а - 11 = -(а - 1) = 1 - а. Значит, в этом <br>случае получаем y(a-lJ = 1 - а. в <br>Пример 5. Упростить выражение ^ • у]32а2 , если a < 0. <br>Решение. Имеем <br>\.Jtf _ ф ¦ \а\ _ 2^2-И <br>^W32a - 2а 2а а " <br>Так как по условию а<0, то |а| = -а. В результате по- <br>лучаем <br>2/2 -lal 2i2-(-a) <br>¦-2^/2. <br>Ответ: -2^2 . <br>Пример 6. Вычислить <br>Решение. Имеем <br>JL/3-2J <br>- 1 <br>Осталось, как обычно говорят, «раскрыть знаки модулей». <br>Воспользуемся тем, что 1 < ,/3 < 2. Значит, ,/3 - 2 < 0, а^/З - 1 > 0. <br>- 11 = >/3 - 1. <br>Но тогда <br>В итоге получаем <br>-(>/3 -2) = 2-^, <br>- 1 = <br>Ответ: 1. <br><br><br><br><br><br><br><br>
| + | [[Image:14-06-146.jpg]]<br><br>Вам ничего не напоминает конструкция, полученная в правой части равенства? Вспомните, ведь точно так же определяется модуль числа а: |
| | + | |
| | + | [[Image:14-06-147.jpg]]<br><br>Значит,[[Image:14-06-144.jpg]] и | а | — одно и то же. Тем самым мы доказали важное тождество: |
| | + | |
| | + | [[Image:14-06-148.jpg]]<br><br>В роли а может выступать любое числовое или алгебраическое выражение. |
| | + | |
| | + | '''Пример 4'''. Упростить выражение [[Image:14-06-149.jpg]] , если: <br>а) а - 1 > 0; б) а - 1 < 0. <br>Решение. Как мы только что установили, справедливо тождество |
| | + | |
| | + | [[Image:14-06-150.jpg]]<br>а) Если а - 1 > 0, то | а - 1| = а - 1. Таким образом, в этом случае получаем [[Image:14-06-151.jpg]] = а - 1. <br>б) Если а - 1 <0, то |а - 1| = -(а - 1) = 1 - а. Значит, в этом случае получаем [[Image:14-06-151.jpg]] = 1 - а. в |
| | + | |
| | + | [[Image:14-06-152.jpg]] |
| | | | |
| | <br> | | <br> |
Версия 12:16, 14 июня 2010
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Модуль действительного числа
МОДУЛЬ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА
1.Модуль действительного числа
и его свойства В младших классах вы уже встречались с понятием модуля (или абсолютной величины) числа, пользовались обозначением | а |. Вы знаете, что, например, | 5 | = 5, | - 3 | = 3. Правда, раньше речь шла только о рациональных числах. Теперь надо
ввести понятие модуля для любого действительного числа.
Определение. Модулем неотрицательного действительного числа х называют само это число: | х | = х; модулем отрицательного действительного числа х называют противоположное число: I х | = - х.
Короче это записывают так:
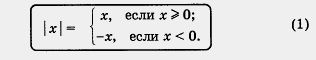
Например,
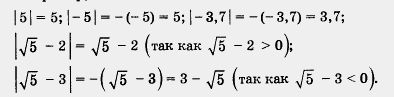
На практике используют различные свойства модулей, например:
1. |а|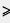 0. 0.
2.|аb| =|a| |b|.
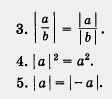
2. Геометрический смысл модуля действительного числа
Вернемся к множеству R действительных чисел и его геометрической модели — числовой прямой. Отметим на прямой две точки а и b (два действительных числа а и b), обозначим через 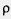 (a, b) расстояние между точками а и b ( (a, b) расстояние между точками а и b (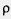 — буква греческого алфавита «ро»). Это расстояние равно b - а, если — буква греческого алфавита «ро»). Это расстояние равно b - а, если
b > а (рис. 101), оно равно а - b, если а > b (рис. 102), наконец, оно равно нулю, если а = b.

Все три случая охватываются одной формулой:
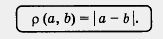
Пример 1. Решить уравнения:
а) | х - 2| = 3; б) | х + 3,2| = 2; в) | х | = 2,7; г) | x - 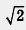 I = 0. I = 0.
Решение, а) Переведем аналитическую модель |х - 2| = 3 на геометрический язык: нам нужно найти на координатной прямой такие точки х, которые удовлетворяют условию 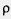 (х, 2) = 3, т. е. удалены от точки 2 на расстояние, равное 3. Это — точки - 1 и 5 (рис. 103). Следовательно, уравнение имеет (х, 2) = 3, т. е. удалены от точки 2 на расстояние, равное 3. Это — точки - 1 и 5 (рис. 103). Следовательно, уравнение имеет
два корня: - 1 и 5.
б) Уравнение | х + 3,2 | = 2 перепишем в виде | х - (— 3,2) | = 2 и далее 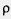 (х, - 3,2) = 2. На координатной прямой есть две точки, которые удалены от точки - 3,2 на расстояние, равное 2. Это — точки - 5,2 и - 1,2 (рис. 104). Значит, уравнение имеет два корня: -5,2 и - 1,2. (х, - 3,2) = 2. На координатной прямой есть две точки, которые удалены от точки - 3,2 на расстояние, равное 2. Это — точки - 5,2 и - 1,2 (рис. 104). Значит, уравнение имеет два корня: -5,2 и - 1,2.
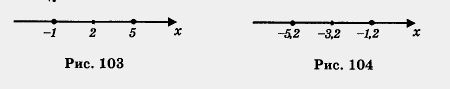
в) Уравнение |x| = 2,7 перепишем в виде |х - 0| = 2,7, или, что то же самое, 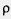 (х, 0) = 2,7. На координатной прямой имеются две точки, которые удалены от точки О на расстояние, равное 2,7. Это — точки - 2,7 и 2,7 (рис. 105). Таким образом, уравнение имеет два корня: - 2,7 и 2,7'. (х, 0) = 2,7. На координатной прямой имеются две точки, которые удалены от точки О на расстояние, равное 2,7. Это — точки - 2,7 и 2,7 (рис. 105). Таким образом, уравнение имеет два корня: - 2,7 и 2,7'.
г) Для уравнения
|х - 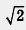 | = 0 можно обойтись без геометрическои иллюстрации, ведь если | а | = 0, то а = 0. Поэтому х - | = 0 можно обойтись без геометрическои иллюстрации, ведь если | а | = 0, то а = 0. Поэтому х - 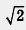 = 0, т. е. х = = 0, т. е. х = 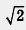 . .
Пример 2. Решить уравнения:
а) |2х - 6| = 8; б) |5 - Зx | = 6; в) |4x + 1| = - 2.
Р е ш е н и е. а) Имеем
|2x - 6| = |2(x -3)| =|2|.| = 2|x -3|
Значит, заданное уравнение можно преобразовать к виду
2|х - 3| = 8, откуда получаем | х - 3| = 4.
Переведем аналитическую модель | х - 3 | = 4 на геометрический язык: нам нужно найти на координатной прямой такие точки х, которые удовлетворяют условию 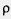 (х, 3) = 4, т. е. удалены от точки 3 на расстояние, равное 4. Это — точки - 1 и 7 (х, 3) = 4, т. е. удалены от точки 3 на расстояние, равное 4. Это — точки - 1 и 7
(рис. 106). Итак, уравнение имеет два корня: - 1 и 7.
б) Имеем
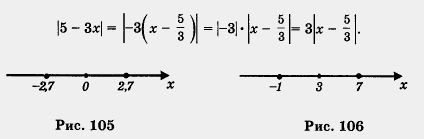
Поэтому заданное уравнение можно преобразовать к виду

Переведем аналитическую модель 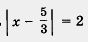 на геометрический язык: нам нужно найти на координатной прямой такие точки х, которые удовлетворяют условию на геометрический язык: нам нужно найти на координатной прямой такие точки х, которые удовлетворяют условию
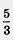
Значит, они удалены от точки  , на расстояние, равное 2. , на расстояние, равное 2.

в) Для уравнения | 4х + 1 | = - 2 никаких преобразований делать не нужно. Оно явно не имеет корней, поскольку в левой его части содержится неотрицательное выражение, а в правой — отрицательное число.
Пример 3. Построить график функции у = |х + 2 |.
Решение. График этой функции получается из графика функции у = | х | сдвигом последнего на две единицы масштаба влево (рис. 111).
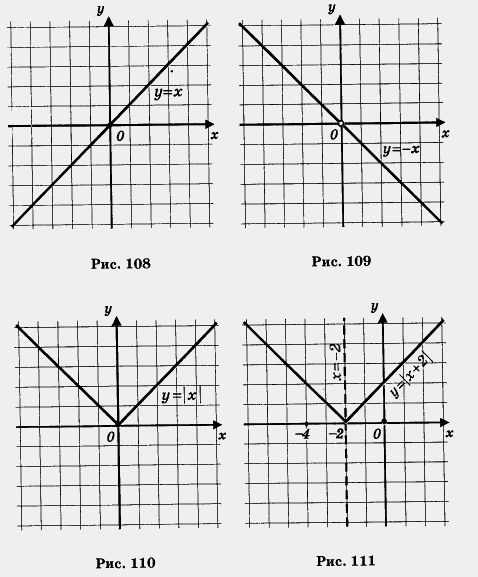
4. Тождество 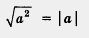
Мы знаем, что если 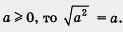 .А как быть, если а < 0? Написать у .А как быть, если а < 0? Написать у 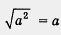 в этом случае нельзя, ведь а < 0 и получится, что в этом случае нельзя, ведь а < 0 и получится, что 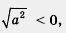 , а это неверно, так как значение квадратного корня не может быть отрицательным. , а это неверно, так как значение квадратного корня не может быть отрицательным.
Чему же равно выражение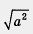 при а < 0? По определению квадратного корня в ответе должно получиться такое число, которое, во-первых, положительно и, во-вторых, при возведении в квадрат дает подкоренное число, т. е. а2. Таким числом будет - а. Смотрите: при а < 0? По определению квадратного корня в ответе должно получиться такое число, которое, во-первых, положительно и, во-вторых, при возведении в квадрат дает подкоренное число, т. е. а2. Таким числом будет - а. Смотрите:
1) - а > 0 (еще раз напомним, что а — отрицательное число, значит, - а — положительное число);
2)(-а)2=а2.
Итак,
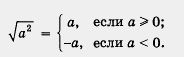
Вам ничего не напоминает конструкция, полученная в правой части равенства? Вспомните, ведь точно так же определяется модуль числа а:

Значит,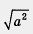 и | а | — одно и то же. Тем самым мы доказали важное тождество: и | а | — одно и то же. Тем самым мы доказали важное тождество:
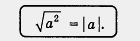
В роли а может выступать любое числовое или алгебраическое выражение.
Пример 4. Упростить выражение 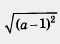 , если: , если:
а) а - 1 > 0; б) а - 1 < 0.
Решение. Как мы только что установили, справедливо тождество
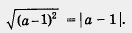
а) Если а - 1 > 0, то | а - 1| = а - 1. Таким образом, в этом случае получаем 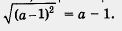 = а - 1. = а - 1.
б) Если а - 1 <0, то |а - 1| = -(а - 1) = 1 - а. Значит, в этом случае получаем 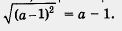 = 1 - а. в = 1 - а. в

Видео по математикескачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|