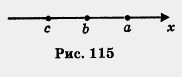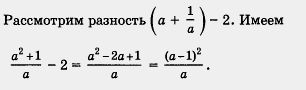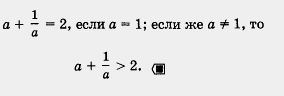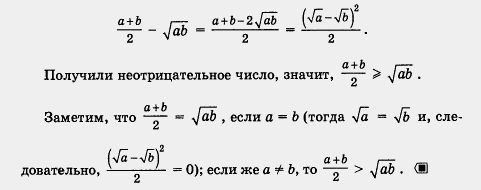|
|
|
| Строка 3: |
Строка 3: |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Свойства числовых неравенств''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Свойства числовых неравенств''' |
| | | | |
| - | '''<br>''' | + | '''<br>''' |
| | | | |
| | + | <br> |
| | | | |
| - | | + | ''' СВОЙСТВА ЧИСЛОВЫХ НЕРАВЕНСТВ '''<br> |
| - | ''' СВОЙСТВА ЧИСЛОВЫХ НЕРАВЕНСТВ '''<br> | + | |
| | | | |
| | <br>Продолжим изучение свойств действительных чисел, начатое в главе 5. Там мы отмечали, что над действительными числами производятся различные арифметические операции, при этом используются свойства таких операций. Знание этих свойств помогало нам выполнять преобразования алгебраических выражений, решать уравнения. | | <br>Продолжим изучение свойств действительных чисел, начатое в главе 5. Там мы отмечали, что над действительными числами производятся различные арифметические операции, при этом используются свойства таких операций. Знание этих свойств помогало нам выполнять преобразования алгебраических выражений, решать уравнения. |
| | | | |
| - | Там же, в главе 5, мы ввели понятие числового неравенства: а> b — это значит, что а - b — положительное число; а < b — это значит, что а - b — отрицательное число. Числовые неравенства обладают рядом свойств, знание которых поможет нам в дальнейшем работать с неравенствами. <br> | + | Там же, в главе 5, мы ввели понятие числового неравенства: а> b — это значит, что а - b — положительное число; а < b — это значит, что а - b — отрицательное число. Числовые неравенства обладают рядом свойств, знание которых поможет нам в дальнейшем работать с неравенствами. <br> |
| | | | |
| - | Для чего нужно уметь решать уравнения, вы знаете: до сих пор математическая модель практически любой реальной ситуации, которую мы рассматривали, представляла собой либо уравнение, либо систему уравнений. На самом деле встречаются и другие математические модели — неравенства, просто мы пока <br>таких ситуаций избегали. <br> | + | Для чего нужно уметь решать уравнения, вы знаете: до сих пор математическая модель практически любой реальной ситуации, которую мы рассматривали, представляла собой либо уравнение, либо систему уравнений. На самом деле встречаются и другие математические модели — неравенства, просто мы пока <br>таких ситуаций избегали. <br> |
| | | | |
| - | Знание свойств числовых неравенств будет полезно и для исследования функций. Например, с неравенствами связаны такие известные вам свойства функций, как наибольшее и наименьшее значения функции на некотором промежутке, ограниченность функции снизу или сверху. С неравенствами связано и <br>свойство возрастания или убывания функции, о котором пойдет речь в одном из следующих параграфов. Так что, как видите, без знания свойств числовых неравенств нам не обойтись. Да вы и сами уже могли убедиться в необходимости умения работать с неравенствами. <br> | + | Знание свойств числовых неравенств будет полезно и для исследования функций. Например, с неравенствами связаны такие известные вам свойства функций, как наибольшее и наименьшее значения функции на некотором промежутке, ограниченность функции снизу или сверху. С неравенствами связано и <br>свойство возрастания или убывания функции, о котором пойдет речь в одном из следующих параграфов. Так что, как видите, без знания свойств числовых неравенств нам не обойтись. Да вы и сами уже могли убедиться в необходимости умения работать с неравенствами. <br> |
| | | | |
| - | Так, в § 27 мы пользовались оценками для числа у[[Image:14-06-194.jpg]] и т. д.), где фактически опирались (хотя и интуитивно) на свойства числовых неравенств. Активно использовали мы знаки (да и свойства) неравенств в § 28 и 30. <br> | + | Так, в § 27 мы пользовались оценками для числа у[[Image:14-06-194.jpg]] и т. д.), где фактически опирались (хотя и интуитивно) на свойства числовых неравенств. Активно использовали мы знаки (да и свойства) неравенств в § 28 и 30. <br> |
| | | | |
| - | Изучением свойств числовых неравенств мы займемся в настоящем параграфе. <br> | + | Изучением свойств числовых неравенств мы займемся в настоящем параграфе. <br> |
| | | | |
| - | '''Свойство 1'''. Если а>b и b> с, то а> с. <br> | + | '''Свойство 1'''. Если а>b и b> с, то а> с. <br> |
| | | | |
| - | <u>Доказательство.</u> По условию, а > b, т. е. а — b — положительное число. Аналогично, так как b > с, делаем вывод, что b - с — положительное число. <br> | + | <u>Доказательство.</u> По условию, а > b, т. е. а — b — положительное число. Аналогично, так как b > с, делаем вывод, что b - с — положительное число. <br> |
| | | | |
| - | Сложив положительные числа а - b и b - с, получим положительное число. Имеем (а - b) + (b - с) - а - с. Значит, а- с — положительное число, т. е. а > с, что и требовалось доказать. <br> | + | Сложив положительные числа а - b и b - с, получим положительное число. Имеем (а - b) + (b - с) - а - с. Значит, а- с — положительное число, т. е. а > с, что и требовалось доказать. <br> |
| | | | |
| - | Свойство 1 можно обосновать, используя геометрическую модель множества действительных чисел, т. е. числовую прямую. Неравенство а> b означает, что на числовой прямой точка а расположена правее точки b, а неравенство b > с — что точка b расположена правее точки с (рис. 115). Но тогда точка о <br>расположена на прямой правее точки с, т. е. а> с. <br> | + | Свойство 1 можно обосновать, используя геометрическую модель множества действительных чисел, т. е. числовую прямую. Неравенство а> b означает, что на числовой прямой точка а расположена правее точки b, а неравенство b > с — что точка b расположена правее точки с (рис. 115). Но тогда точка о <br>расположена на прямой правее точки с, т. е. а> с. <br> |
| | | | |
| - | [[Image:14-06-195.jpg]]<br> | + | [[Image:14-06-195.jpg]]<br> |
| | | | |
| - | Свойство 1 обычно называют свой ством транзитивности (образно с говоря, от пункта а мы добираемся до Рис. 115 пункта с как бы транзитом, с промежуточной остановкой в пункте b). <br> | + | Свойство 1 обычно называют свой ством транзитивности (образно с говоря, от пункта а мы добираемся до Рис. 115 пункта с как бы транзитом, с промежуточной остановкой в пункте b). <br> |
| | | | |
| - | '''Свойство 2'''. Если а>b, то а + с>Ь + с. <br> | + | '''Свойство 2'''. Если а>b, то а + с>Ь + с. <br> |
| | | | |
| - | '''Свойство 3.''' Если а>b и m> О, то от > bm; <br>если а>b и m < o, то am < bm. <br>Смысл свойства 3 заключается в следующем: если обе части неравенства умножить на одно и то же положительное число, то знак неравенства следует сохранить; <br>'''''если обе части неравенства умножить на одно и то же отрицательное число, то знак неравенства следует изменить (< на >,> на< ).'''''<br> | + | '''Свойство 3.''' Если а>b и m> О, то от > bm; <br>если а>b и m < o, то am < bm. <br>Смысл свойства 3 заключается в следующем: если обе части неравенства умножить на одно и то же положительное число, то знак неравенства следует сохранить; <br>'''''если обе части неравенства умножить на одно и то же отрицательное число, то знак неравенства следует изменить (< на >,> на< ).'''''<br> |
| | | | |
| | То же относится к делению обеих частей неравенства на одно и то же положительное или отрицательное число т, поскольку деление на m всегда можно заменить умножением на [[Image:14-06-196.jpg]] . <br>Из свойства 3, в частности, следует, что, умножив обе части неравенства а > b на — 1, получим — а < -b. Это значит, что если изменить знаки у обеих частей неравенства, то надо изменить и знак неравенства: если а>b, то — а <—b. | | То же относится к делению обеих частей неравенства на одно и то же положительное или отрицательное число т, поскольку деление на m всегда можно заменить умножением на [[Image:14-06-196.jpg]] . <br>Из свойства 3, в частности, следует, что, умножив обе части неравенства а > b на — 1, получим — а < -b. Это значит, что если изменить знаки у обеих частей неравенства, то надо изменить и знак неравенства: если а>b, то — а <—b. |
| Строка 67: |
Строка 67: |
| | [[Image:14-06-199.jpg]]<br><br>По условию, а, b, а - b — положительные числа. Значит, [[Image:14-06-200.jpg]] — отрицательное число, т.е. —[[Image:14-06-201.jpg]], откуда следует, что [[Image:14-06-202.jpg]]<br><br>'''Пример 2.''' Пусть а — положительное число. Доказать, что [[Image:14-06-203.jpg]]<br>Решение. | | [[Image:14-06-199.jpg]]<br><br>По условию, а, b, а - b — положительные числа. Значит, [[Image:14-06-200.jpg]] — отрицательное число, т.е. —[[Image:14-06-201.jpg]], откуда следует, что [[Image:14-06-202.jpg]]<br><br>'''Пример 2.''' Пусть а — положительное число. Доказать, что [[Image:14-06-203.jpg]]<br>Решение. |
| | | | |
| - | [[Image:14-06-204.jpg]] | + | [[Image:14-06-204.jpg]] |
| | + | |
| | + | <br> Получили неотрицательное число, значит, [[Image:14-06-205.jpg]]<br>Заметим, что [[Image:14-06-206.jpg]]<br><br>'''Пример 3.''' Пусть а и b неотрицательные числа. <br>Доказать, что [[Image:14-06-207.jpg]]<br>Решение. Составим разность левой и правой частей неравенства. Имеем |
| | + | |
| | + | [[Image:14-06-208.jpg]]<br><br>Число [[Image:14-06-209.jpg]] называют средним арифметическим чисел а и b число [[Image:14-06-210.jpg]] называют средним геометрическим чисел а и b. Таким образом, неравенство, доказанное в примере 3, означает, что среднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического. Доказанное <br>неравенство иногда называют неравенством Коши в честь французского математика XIX века Огюста Коши. |
| | + | |
| | + | '''''Замечание 2'''''. Неравенство Коши имеет любопытное геометрическое истолкование. Пусть дан прямоугольный треугольник и пусть высота h, проведенная из вершины прямого угла, делит гипотенузу на отрезки а и b (рис. 116). В геометрии доказано, что |
| | + | |
| | + | [[Image:14-06-211.jpg]]<br><br>[[Image:14-06-212.jpg]] (так что не случайно для этого выражения ввели термин «среднее геометрическое»). А что такое [[Image:14-06-213.jpg]] ? Это длина половины гипотенузы. Но из <br>геометрии известно, что медиана m прямоугольного треугольника, проведенная из вершины прямого угла, как раз и равна половине гипотенузы. Таким <br>образом, неравенство Коши означает, что медиана, проведенная к гипотенузе (т. е. [[Image:14-06-213.jpg]]), не меньше высоты, проведенной к гипотенузе (т.е. [[Image:14-06-214.jpg]]), — <br>очевидный геометрический факт (см. рис. 116). Свойства числовых неравенств позволяют сравнивать действительные числа по величине, оценивать результат. |
| | + | |
| | + | '''Пример 4.''' Сравнить числа: |
| | + | |
| | + | [[Image:14-06-215.jpg]]<br><br>Решение, а) Поставим между сравниваемыми числами знак < ; интуиция подсказывает, что первое число меньше второго. Если в результате правильных (т. е. строгих, основанных на свойствах числовых неравенств) рассуждений мы получим верное неравенство, то наша догадка подтвердится. |
| | + | |
| | + | Если же в результате правильных рассуждений мы получим неверное неравенство, то между заданными числами надо было поставить не знак <, а знак > (или = , если окажется, что числа равны). |
| | | | |
| - | <br> Получили неотрицательное число, значит, [[Image:14-06-205.jpg]]<br>Заметим, что [[Image:14-06-206.jpg]]<br><br>Доказать, что <br>а+Ь <br>неотрицательные числа. <br>> Jab. <br>Решение. Составим разность левой и правой частей <br>неравенства. Имеем <br>п <br>a + b-2Jab (VVb) <br>~ <br>тт й + Ь - <br>Получили неотрицательное число, значит, —г— -, <br>Заметим, что —г— = •Jab , если а — b (тогда \[а = Jb и, еле- <br>довательно, <br>a+b <br>a+b I— <br>0); если же аФЪ,чо —г- > yjab . (Й <br>Число <br>а+Ь <br>называют средним арифмети- <br>среднее <br>арифмети- <br>ческое <br>среднее <br>геометри- <br>ческое <br>неравенство <br>Коши <br>ческим чисел а и Ъ\ число -Jab называют <br>средним геометрическим чисел а и Ъ. Таким <br>образом, неравенство, доказанное в примере 3, <br>означает, что среднее арифметическое двух <br>неотрицательных чисел не меньше их сред- <br>него геометрического. Доказанное <br>неравенство иногда называют неравенством <br>Коши в честь французского математика XIX <br>века Огюста Коши. <br>ЗзМ6ЧанИ& 2. Неравенство Коши имеет любо- <br>пытное геометрическое истолкование. Пусть дан <br>прямоугольный треугольник и пусть высота h, прове- <br>денная из вершины прямого угла, делит гипотенузу на <br>отрезки а и Ь (рис. 116). В геометрии доказано, что <br>НЕРАВЕНСТВА <br>Рис. 116 <br>h = -Jab (так что не случайно для этого выражения <br>ввели термин «среднее геометрическое»). А что <br>а + Ь <br>такое —— ? Это длина половины гипотенузы. Но из <br>геометрии известно, что медиана т прямоугольного <br>треугольника, проведенная из вершины прямого <br>угла, как раз и равна половине гипотенузы. Таким <br>образом, неравенство Коши означает, что медиана, <br>а + Ь <br>проведенная к гипотенузе (т. е. <br>), не меньше <br>высоты, проведенной к гипотенузе (т.е. *Jab), — <br>очевидный геометрический факт (см. рис. 116). <br>Свойства числовых неравенств позволяют сравнивать <br>действительные числа по величине, оценивать результат. <br>Пример 4. Сравнить числа: <br>в) тс + <br>и 4 + <br>Решение, а) Поставим между сравниваемыми числами <br>знак < ; интуиция подсказывает, что первое число меньше <br>второго. Если в результате правильных (т. е. строгих, <br>основанных на свойствах числовых неравенств) рассуждений мы <br>получим верное неравенство, то наша догадка подтвердится. <br>Если же в результате правильных рассуждений мы получим <br>неверное неравенство, то между заданными числами надо было <br>поставить не знак <, а знак > (или = , если окажется, что числа <br>равны). <br>Итак, мы считаем, что /б < л/7 • Тогда, согласно свойству 6, <br>у </б ) <\ л/7 ) , т. е. 5 < 7. Это верное неравенство, значит, наша <br>догадка подтвердилась: ^5 < д/7 . <br>б) Поставим между сравниваемыми числами наугад знак > <br>(тут уже действительно наугад, поскольку интуиция здесь не <br>поможет), т. е. предположим, что ^3 + ^/б > 2 + ^5 • Возве- <br>дя обе части неравенства в квадрат и используя свойство 6, <br>получим (л/3 + ^/6 J > B + 75 J, <br>6>4 + 47б +5, <br>Воспользовавшись свойством 2, прибавим к обеим частям <br>этого неравенства число -9; получим <br>9>9 + 47б -9, т.е. <br>Разделив обе части этого неравенства на положительное <br>число 2, получим (в силу свойства 3) ,/18 > 2 ^5 • Еще раз <br>воспользуемся свойством 6: ( ^18 J > B 7б J, т. е. 18 > 20. Это <br>неверно, наша догадка не подтвердилась. Значит, надо было <br>использовать не знак >, а знак <. <br>Итак, ./I + ^6 < 2 + 75 . <br>в) А в этом примере можно не гадать. Имеем тс < 4, ^До < Л/ТТ . <br>Применив к этим двум неравенствам одинакового смысла свой- <br>ство 4 (о почленном сложении), получим тс + ^До < 4 + Til • ® <br>Пример 5. Известно, что 2,1 < а < 2,2; 3,7 < Ъ < 3,8. <br>Найти оценки для числа: <br>а) 2а; б) - ЗЬ; в) а + Ь; г) а - Ъ; д) а2; е) Ъ3; ж) -. <br>Решение, а) Умножив все части двойного неравенства <br>2,1<а<2,2на одно и то же положительное число 2, получим <br>2 • 2,1 < 2а < 2 • 2,2, т. е. 4,2 <2а< 4,4. <br>б) Умножив все части двойного неравенства 3,7 < b < 3,8 на <br>одно и то же отрицательное число - 3, получим неравенство <br>противоположного смысла: <br>- 3 • 3,7 > - ЗЬ > - 3 • 3,8, т. е. - 11,4 < - 36 < - 11,1 <br>(вместо записи вида а > Ъ > с мы перешли к более <br>употребительной записи с <Ъ < а). <br>в) Сложив почленно заданные двойные неравенства <br>одинакового смысла, получим <br>2,1 <а<2,2 <br>+ 3,7 < Ъ < 3,8 <br>5,8 < а + Ъ < 6,0. <br>г) Сначала умножим все части двойного неравенства 3,7 < Ъ < <br>< 3,8 на одно и то же отрицательное число -1; получим <br>неравенство противоположного смысла <br>- 3,7 > - Ъ > - 3,8, т. е. - 3,8 < - Ь < - 3,7. <br>Далее имеем <br>2,1 < а <2,2 <br>+ -3,8<-Ь<-3,7 <br>д) Поскольку все части двойного неравенства 2,1 < а < 2,2 <br>положительны, возведя их в квадрат, получим <br>2,12<а2<2,22, <br>т. е. <br>4,41 < а2 < 4,84. <br>е) Возведя в куб все части двойного неравенства 3,7 < b < 3,8, <br>получим <br>3,73 < Ъ3 < 3,83, <br>т. е. <br>50,653 < Ь3 < 54,872. <br>ж) В примере 1 мы установили, что если' а и Ъ — <br>положительные числа, то из неравенства а < Ъ следует <br>неравенство противоположного смысла - > -. Значит из <br>а Ь <br>двойного неравенства 2,1 < а < 2,2 следует, что <br>J_ I J_ <br>2,1 > а > 2,2 ' <br>т. е. <br>5 1 10 <br>§ 34. РЕШЕНИЕ ЛИНЕЙНЫХ <br><br><br><br><br><br><br><br><br>
| + | Итак, мы считаем, что /б < л/7 • Тогда, согласно свойству 6, <br>у </б ) <\ л/7 ) , т. е. 5 < 7. Это верное неравенство, значит, наша <br>догадка подтвердилась: ^5 < д/7 . <br>б) Поставим между сравниваемыми числами наугад знак > <br>(тут уже действительно наугад, поскольку интуиция здесь не <br>поможет), т. е. предположим, что ^3 + ^/б > 2 + ^5 • Возве- <br>дя обе части неравенства в квадрат и используя свойство 6, <br>получим (л/3 + ^/6 J > B + 75 J, <br>6>4 + 47б +5, <br>Воспользовавшись свойством 2, прибавим к обеим частям <br>этого неравенства число -9; получим <br>9>9 + 47б -9, т.е. <br>Разделив обе части этого неравенства на положительное <br>число 2, получим (в силу свойства 3) ,/18 > 2 ^5 • Еще раз <br>воспользуемся свойством 6: ( ^18 J > B 7б J, т. е. 18 > 20. Это <br>неверно, наша догадка не подтвердилась. Значит, надо было <br>использовать не знак >, а знак <. <br>Итак, ./I + ^6 < 2 + 75 . <br>в) А в этом примере можно не гадать. Имеем тс < 4, ^До < Л/ТТ . <br>Применив к этим двум неравенствам одинакового смысла свой- <br>ство 4 (о почленном сложении), получим тс + ^До < 4 + Til • ® <br>Пример 5. Известно, что 2,1 < а < 2,2; 3,7 < Ъ < 3,8. <br>Найти оценки для числа: <br>а) 2а; б) - ЗЬ; в) а + Ь; г) а - Ъ; д) а2; е) Ъ3; ж) -. <br>Решение, а) Умножив все части двойного неравенства <br>2,1<а<2,2на одно и то же положительное число 2, получим <br>2 • 2,1 < 2а < 2 • 2,2, т. е. 4,2 <2а< 4,4. <br>б) Умножив все части двойного неравенства 3,7 < b < 3,8 на <br>одно и то же отрицательное число - 3, получим неравенство <br>противоположного смысла: <br>- 3 • 3,7 > - ЗЬ > - 3 • 3,8, т. е. - 11,4 < - 36 < - 11,1 <br>(вместо записи вида а > Ъ > с мы перешли к более <br>употребительной записи с <Ъ < а). <br>в) Сложив почленно заданные двойные неравенства <br>одинакового смысла, получим <br>2,1 <а<2,2 <br>+ 3,7 < Ъ < 3,8 <br>5,8 < а + Ъ < 6,0. <br>г) Сначала умножим все части двойного неравенства 3,7 < Ъ < <br>< 3,8 на одно и то же отрицательное число -1; получим <br>неравенство противоположного смысла <br>- 3,7 > - Ъ > - 3,8, т. е. - 3,8 < - Ь < - 3,7. <br>Далее имеем <br>2,1 < а <2,2 <br>+ -3,8<-Ь<-3,7 <br>д) Поскольку все части двойного неравенства 2,1 < а < 2,2 <br>положительны, возведя их в квадрат, получим <br>2,12<а2<2,22, <br>т. е. <br>4,41 < а2 < 4,84. <br>е) Возведя в куб все части двойного неравенства 3,7 < b < 3,8, <br>получим <br>3,73 < Ъ3 < 3,83, <br>т. е. <br>50,653 < Ь3 < 54,872. <br>ж) В примере 1 мы установили, что если' а и Ъ — <br>положительные числа, то из неравенства а < Ъ следует <br>неравенство противоположного смысла - > -. Значит из <br>а Ь <br>двойного неравенства 2,1 < а < 2,2 следует, что <br>J_ I J_ <br>2,1 > а > 2,2 ' <br>т. е. <br>5 1 10 <br>§ 34. РЕШЕНИЕ ЛИНЕЙНЫХ <br><br><br><br><br><br><br><br><br> |
| | | | |
| - | <br> | + | <br> |
| | | | |
| | <sub>Книги и учебники согласно календарному плануванння по математике 8 класса [[Математика|скачать]], помощь школьнику [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | | <sub>Книги и учебники согласно календарному плануванння по математике 8 класса [[Математика|скачать]], помощь школьнику [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
Версия 17:59, 14 июня 2010
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Свойства числовых неравенств
СВОЙСТВА ЧИСЛОВЫХ НЕРАВЕНСТВ
Продолжим изучение свойств действительных чисел, начатое в главе 5. Там мы отмечали, что над действительными числами производятся различные арифметические операции, при этом используются свойства таких операций. Знание этих свойств помогало нам выполнять преобразования алгебраических выражений, решать уравнения.
Там же, в главе 5, мы ввели понятие числового неравенства: а> b — это значит, что а - b — положительное число; а < b — это значит, что а - b — отрицательное число. Числовые неравенства обладают рядом свойств, знание которых поможет нам в дальнейшем работать с неравенствами.
Для чего нужно уметь решать уравнения, вы знаете: до сих пор математическая модель практически любой реальной ситуации, которую мы рассматривали, представляла собой либо уравнение, либо систему уравнений. На самом деле встречаются и другие математические модели — неравенства, просто мы пока
таких ситуаций избегали.
Знание свойств числовых неравенств будет полезно и для исследования функций. Например, с неравенствами связаны такие известные вам свойства функций, как наибольшее и наименьшее значения функции на некотором промежутке, ограниченность функции снизу или сверху. С неравенствами связано и
свойство возрастания или убывания функции, о котором пойдет речь в одном из следующих параграфов. Так что, как видите, без знания свойств числовых неравенств нам не обойтись. Да вы и сами уже могли убедиться в необходимости умения работать с неравенствами.
Так, в § 27 мы пользовались оценками для числа у и т. д.), где фактически опирались (хотя и интуитивно) на свойства числовых неравенств. Активно использовали мы знаки (да и свойства) неравенств в § 28 и 30. и т. д.), где фактически опирались (хотя и интуитивно) на свойства числовых неравенств. Активно использовали мы знаки (да и свойства) неравенств в § 28 и 30.
Изучением свойств числовых неравенств мы займемся в настоящем параграфе.
Свойство 1. Если а>b и b> с, то а> с.
Доказательство. По условию, а > b, т. е. а — b — положительное число. Аналогично, так как b > с, делаем вывод, что b - с — положительное число.
Сложив положительные числа а - b и b - с, получим положительное число. Имеем (а - b) + (b - с) - а - с. Значит, а- с — положительное число, т. е. а > с, что и требовалось доказать.
Свойство 1 можно обосновать, используя геометрическую модель множества действительных чисел, т. е. числовую прямую. Неравенство а> b означает, что на числовой прямой точка а расположена правее точки b, а неравенство b > с — что точка b расположена правее точки с (рис. 115). Но тогда точка о
расположена на прямой правее точки с, т. е. а> с.
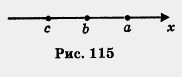
Свойство 1 обычно называют свой ством транзитивности (образно с говоря, от пункта а мы добираемся до Рис. 115 пункта с как бы транзитом, с промежуточной остановкой в пункте b).
Свойство 2. Если а>b, то а + с>Ь + с.
Свойство 3. Если а>b и m> О, то от > bm;
если а>b и m < o, то am < bm.
Смысл свойства 3 заключается в следующем: если обе части неравенства умножить на одно и то же положительное число, то знак неравенства следует сохранить;
если обе части неравенства умножить на одно и то же отрицательное число, то знак неравенства следует изменить (< на >,> на< ).
То же относится к делению обеих частей неравенства на одно и то же положительное или отрицательное число т, поскольку деление на m всегда можно заменить умножением на 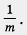 . .
Из свойства 3, в частности, следует, что, умножив обе части неравенства а > b на — 1, получим — а < -b. Это значит, что если изменить знаки у обеих частей неравенства, то надо изменить и знак неравенства: если а>b, то — а <—b.
Свойство 4. Если а>b и c> d, то а + с > b + d.
Доказательство.
I способ. По условию, а > b и с > d, значит, а - b и с - d — положительные числа. Тогда и их сумма, т. е. (а - b) + (с - d) — положительное число. Так как
(a-b) + (c-d) = (a + c)-(b + d), то и (а + с) - (b + d) — положительное число. Поэтому a + c>b + d.
II способ. Так как а > Ь, то, согласно свойству 2, а + с > b + с. Аналогично, так как с > d, то с + b > d + b.
Итак, а + с > b + с, b + с > b + d. Тогда, в силу свойства транзитивности, получаем, что а + с > b + d.
Замечание 1. Мы привели два способа доказательства для того, чтобы вы сами выбрали тот из них, который вам больше понравился или более понятен.
Кроме того, вообще полезно знакомиться с различными обоснованиями одного и того же факта.
Доказательство. Так как а > b и с > 0, то ас > bc. Аналогично, так как с > d и b > o, то cb > db. Итак, ас > bc, bc > bd. Тогда, согласно свойству транзитивности, получаем, что ас > bd.
Обычно неравенства вида а > b, с > d (или а < с, с < d) называют неравенствами одинакового смысла, а неравенства а > b и с < d — неравенствами противоположного смысла.
Свойство 5 означает, что при умножении неравенств одинакового смысла, у которых левые и правые части — положительные числа, получится неравенство того же смысла.
Свойство 6. Если а и b — неотрицательные числа и а > b, то аn > Ьn, где n — любое натуральное число.
Смысл свойства 6 заключается в следующем: если обе части неравенства — неотрицательные числа, то их можно возвести в одну и ту же натуральную степень, сохранив знак неравенства.
Дополнение к свойству 6. Если n — нечетное число, то для любых чисел а и b из неравенства а > b следует неравенство того же смысла аn > bn.
Вы обратили внимание на то, что в приведенных доказательствах мы пользовались по сути дела всего двумя идеями? Первая идея — составить разность левой и правой частей неравенства и выяснить, какое число получится: положительное или отрицательное. Вторая идея — для доказательства нового свойства использовать уже известные свойства. Так поступают и в других случаях доказательств числовых неравенств: например, так можно доказать те из перечисленных выше свойств, которые мы здесь привели без доказательства (советуем вам в качестве упражнения попробовать восполнить этот пробел).
Рассмотрим несколько примеров.
Пример 1. Пусть а и b — положительные числа и а > b.
Доказать, что
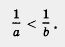
Решение. Рассмотрим разность .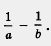 Имеем Имеем
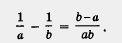
По условию, а, b, а - b — положительные числа. Значит, 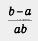 — отрицательное число, т.е. — — отрицательное число, т.е. —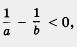 , откуда следует, что , откуда следует, что 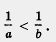
Пример 2. Пусть а — положительное число. Доказать, что 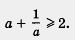
Решение.
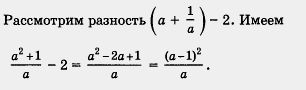
Получили неотрицательное число, значит, 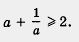
Заметим, что 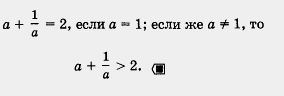
Пример 3. Пусть а и b неотрицательные числа.
Доказать, что 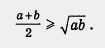
Решение. Составим разность левой и правой частей неравенства. Имеем
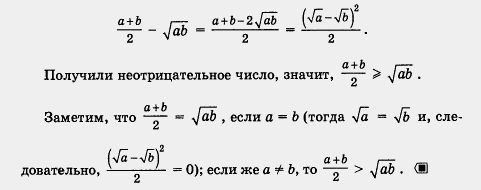
Число 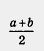 называют средним арифметическим чисел а и b число называют средним арифметическим чисел а и b число 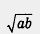 называют средним геометрическим чисел а и b. Таким образом, неравенство, доказанное в примере 3, означает, что среднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического. Доказанное называют средним геометрическим чисел а и b. Таким образом, неравенство, доказанное в примере 3, означает, что среднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического. Доказанное
неравенство иногда называют неравенством Коши в честь французского математика XIX века Огюста Коши.
Замечание 2. Неравенство Коши имеет любопытное геометрическое истолкование. Пусть дан прямоугольный треугольник и пусть высота h, проведенная из вершины прямого угла, делит гипотенузу на отрезки а и b (рис. 116). В геометрии доказано, что
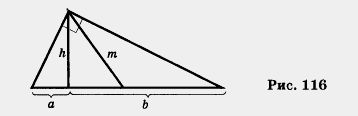
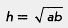 (так что не случайно для этого выражения ввели термин «среднее геометрическое»). А что такое (так что не случайно для этого выражения ввели термин «среднее геометрическое»). А что такое 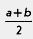 ? Это длина половины гипотенузы. Но из ? Это длина половины гипотенузы. Но из
геометрии известно, что медиана m прямоугольного треугольника, проведенная из вершины прямого угла, как раз и равна половине гипотенузы. Таким
образом, неравенство Коши означает, что медиана, проведенная к гипотенузе (т. е. 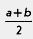 ), не меньше высоты, проведенной к гипотенузе (т.е. ), не меньше высоты, проведенной к гипотенузе (т.е. 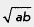 ), — ), —
очевидный геометрический факт (см. рис. 116). Свойства числовых неравенств позволяют сравнивать действительные числа по величине, оценивать результат.
Пример 4. Сравнить числа:
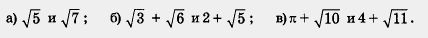
Решение, а) Поставим между сравниваемыми числами знак < ; интуиция подсказывает, что первое число меньше второго. Если в результате правильных (т. е. строгих, основанных на свойствах числовых неравенств) рассуждений мы получим верное неравенство, то наша догадка подтвердится.
Если же в результате правильных рассуждений мы получим неверное неравенство, то между заданными числами надо было поставить не знак <, а знак > (или = , если окажется, что числа равны).
Итак, мы считаем, что /б < л/7 • Тогда, согласно свойству 6,
у </б ) <\ л/7 ) , т. е. 5 < 7. Это верное неравенство, значит, наша
догадка подтвердилась: ^5 < д/7 .
б) Поставим между сравниваемыми числами наугад знак >
(тут уже действительно наугад, поскольку интуиция здесь не
поможет), т. е. предположим, что ^3 + ^/б > 2 + ^5 • Возве-
дя обе части неравенства в квадрат и используя свойство 6,
получим (л/3 + ^/6 J > B + 75 J,
6>4 + 47б +5,
Воспользовавшись свойством 2, прибавим к обеим частям
этого неравенства число -9; получим
9>9 + 47б -9, т.е.
Разделив обе части этого неравенства на положительное
число 2, получим (в силу свойства 3) ,/18 > 2 ^5 • Еще раз
воспользуемся свойством 6: ( ^18 J > B 7б J, т. е. 18 > 20. Это
неверно, наша догадка не подтвердилась. Значит, надо было
использовать не знак >, а знак <.
Итак, ./I + ^6 < 2 + 75 .
в) А в этом примере можно не гадать. Имеем тс < 4, ^До < Л/ТТ .
Применив к этим двум неравенствам одинакового смысла свой-
ство 4 (о почленном сложении), получим тс + ^До < 4 + Til • ®
Пример 5. Известно, что 2,1 < а < 2,2; 3,7 < Ъ < 3,8.
Найти оценки для числа:
а) 2а; б) - ЗЬ; в) а + Ь; г) а - Ъ; д) а2; е) Ъ3; ж) -.
Решение, а) Умножив все части двойного неравенства
2,1<а<2,2на одно и то же положительное число 2, получим
2 • 2,1 < 2а < 2 • 2,2, т. е. 4,2 <2а< 4,4.
б) Умножив все части двойного неравенства 3,7 < b < 3,8 на
одно и то же отрицательное число - 3, получим неравенство
противоположного смысла:
- 3 • 3,7 > - ЗЬ > - 3 • 3,8, т. е. - 11,4 < - 36 < - 11,1
(вместо записи вида а > Ъ > с мы перешли к более
употребительной записи с <Ъ < а).
в) Сложив почленно заданные двойные неравенства
одинакового смысла, получим
2,1 <а<2,2
+ 3,7 < Ъ < 3,8
5,8 < а + Ъ < 6,0.
г) Сначала умножим все части двойного неравенства 3,7 < Ъ <
< 3,8 на одно и то же отрицательное число -1; получим
неравенство противоположного смысла
- 3,7 > - Ъ > - 3,8, т. е. - 3,8 < - Ь < - 3,7.
Далее имеем
2,1 < а <2,2
+ -3,8<-Ь<-3,7
д) Поскольку все части двойного неравенства 2,1 < а < 2,2
положительны, возведя их в квадрат, получим
2,12<а2<2,22,
т. е.
4,41 < а2 < 4,84.
е) Возведя в куб все части двойного неравенства 3,7 < b < 3,8,
получим
3,73 < Ъ3 < 3,83,
т. е.
50,653 < Ь3 < 54,872.
ж) В примере 1 мы установили, что если' а и Ъ —
положительные числа, то из неравенства а < Ъ следует
неравенство противоположного смысла - > -. Значит из
а Ь
двойного неравенства 2,1 < а < 2,2 следует, что
J_ I J_
2,1 > а > 2,2 '
т. е.
5 1 10
§ 34. РЕШЕНИЕ ЛИНЕЙНЫХ
Книги и учебники согласно календарному плануванння по математике 8 класса скачать, помощь школьнику онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|