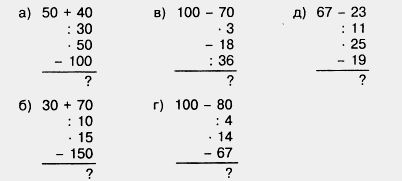Версия 16:09, 15 июня 2010

Гипермаркет знаний>>Математика>>Математика 5 класс>>Математика:Буквенная запись свойств сложения и вычитания

                                 Буквенная запись свойств сложения и вычитания

Известные вам свойства сложения и вычитания можно записать с помощью букв.
1. Переместительное свойство сложения записывают так:
а + b = b + а.
В этом равенстве буквы а и b могут принимать любые натуральные значения и значение 0.

2. Сочетательное свойство сложения записывают с помощью букв так:
a + (b + с) = (а + b) + с = а + b + с.
Здесь а, b и с — любые натуральные числа или нуль.

3. Свойство нуля при сложении можно записать так: Здесь буква а может иметь любое значение.

4. Свойство вычитания суммы из числа записывают с помощью букв еледующим образом:
a — (b + с) = a — b — с.
Здесь b + с < а или b + с = а.

5. Свойство вычитания числа из суммы записывают с помощью букв так:

(а + b) - с = а + (b - с), если с < Ь или о = b;
(а + b) - с = (а - с) + Ь, если с < а или с = а.

6. Свойства нуля при вычитании можно записать так:
а — 0 = а; а — а = 0.
Здесь а может принимать любые натуральные значения и значение 0.
 Прочитайте записанные с помощью букв свойства сложения и вычитания.

337. Запишите сочетательное свойство сложения с помощью букв а, b и с. Замените буквы их значениями: a = 9873, b = 6914, с = 10 209 — и проверьте получившееся числовое равенство.

338. Запишите свойство вычитания суммы из числа с помощью букв a, b и с. Замените буквы их значениями: a = 243, b = 152, с = 88 — и проверьте получившееся числовое равенство.

339. Запишите свойство вычитания числа из суммы двумя способами. Проверьте получившиеся числовые равенства, заменив буквы их значениями:

a) a = 98, b = 47 и с = 58;

б) а = 93, b = 97 и с = 95.

340. а) На рисунке 42 с помощью циркуля найдите точки М(а + b) и N(а - b).

б) Объясните по рисунку 43 смысл сочетательного свойства сложения.

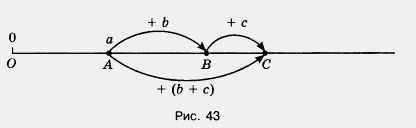
в) Объясните с помощью рисунков остальные свойства сложения и вычитания.

341. Из свойств сложения следует:

56 + х + 14 = х + 56 + 14 = x + (56 + 14) = х + 70.

По этому образцу упростите выражение:

а) 23 + 49 + m;                         в) х + 54 + 27;
б) 38 + n + 27;                          г) 176 4- у + 24.

342. Найдите значение выражения, предварительно упростив его:

а) 28 + m + 72 при m = 87;                         в) 228 + k + 272 при k = 48;
б) n + 49 + 151 при n = 63;                         г) 349 + р + 461 при р = 115.

343. Из свойств вычитания следует:

28 - (15 + с) = 28 - 15 - с = 13 - с,
а - 64 - 26 = а - (64 + 26) = а - 90.

Какое свойство вычитания применено в этих примерах? Используя это свойство вычитания, упростите выражение:

а) 35 - (18 + у);

б) m- 128 - 472.

344. Из свойств сложения и вычитания следует:

137 - с - 27 « 137 - (с + 27) = 137 - (27 + с) = 137 - 27 - с = 110 - с.

Какие свойства сложения и вычитания применены в этом примере?
Используя эти свойства, упростите выражение:

а) 168 - (х + 47);
б) 384 - m - 137.

345. Из свойств вычитания следует:

(154 + b) - 24 = (154 - 24) + b = 130 + b;
а - 10 + 15 = (а - 10) + 15 = (а + 15) - 10 = а + (15 - 10) = a + 5.

Какое свойство вычитания применяется в этом примере?
Используя это свойство, упростите выражение:

а) (248 + m) - 24;                     в) b + 127 - 84;                     д) (12 - k) + 24;
б) 189 + n - 36;                        г) а - 30 + 55;                        е) х - 18 + 25.

346. Найдите значение выражения, предварительно упростив его:

а) а - 28 - 37 при а = 265;                       в) 237 + с + 163 при с = 194; 188;
б) 149 + b - 99 при b = 77;                      г) d - 135 + 165 при d = 239; 198.

347. На отрезке АВ отмечены точки С и D, причем точка С лежит между точками А и D. Составьте выражение для длины отрезка:

а) АВ если АС = 453 мм, CD = х мм и DB = 65 мм. Найдите значение получившегося выражения при х = 315; 283.
б) АС, если АВ = 214 мм, CD = 84 мм и DB = у мм. Найдите значение получившегося выражения при у = 28; 95.

348. Токарь выполнил заказ на изготовление одинаковых деталей за три дня. В первый день он изготовил 23 детали, во второй день — на b деталей больше, чем в первый день, а в третий день — на четыре детали меньше, чем в первый день. Сколько деталей изготовил токарь за эти три дня? Составьте выражение для решения задачи и найдите его значение при b = 7 и b = 9.

349. Вычислите устно:

 

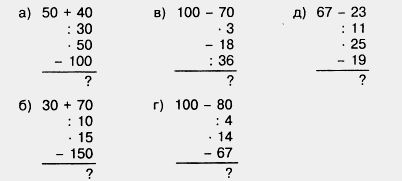
350. Найдите половину, четверть и треть каждого из чисел: 12; 36; 60; 84; 120.

351. Придумайте задачу, решением которой является выражение:
а) (47 - 15) + (62 - 12); б) х + (39 - 14); в) 81 - (х + у).

352. Среди чисел 1874, 29 769, 1875, 30 759 найдите то, которое является значением разности:
а) 30 462 - 693; б) 2567 - 693;

в) 31 452 - 693; г) 2568 - 693.

353. Как изменится сумма, если:

а) одно из слагаемых увеличить на 5;
б) одно слагаемое увеличить на 5, а второе — на 10;
в) одно слагаемое увеличить на 6, а второе уменьшить на 6;
г) одно из слагаемых увеличить вдвое?

354. Найдите пропущенные числа:

355. Подумайте, в чем сходство и в чем различие:
а) отрезка и луча; б) луча и прямой.
356. Сколько двузначных чисел можно составить из цифр 1, 3, 5, 7, 9,
если цифры в записи числа не повторяются?
Сколько трехзначных чисел можно составить из тех же цифр (цифры в
записи числа не повторяются)?
357. Найдите площадь двухкомнатной квартиры, если площадь обеих ком-
нат 35 м2, площадь кухни 9 м2, а подсобные помещения имеют общую пло-
щадь а м2. Составьте выражение для решения задачи и найдите его значение
при а - 8 и а = 12.
358. У Пети 180 марок в трех альбомах. В одном альбоме 95 марок,
а в другом у марок. Сколько марок у Пети в третьем альбоме? Составьте вы-
ражение для решения задачи и найдите его значение при у = 40; 45; 62.
359. В сарае было 138 т сена. В первый месяц израсходовали 49 т сена,
а во второй месяц — на х т больше. Сколько тонн сена осталось в сарае?
Составьте выражение для решения задачи и найдите его значение при х =
= 14; 20; 30.
360. Подчеркните уменьшаемое одной чертой, а вычитаемое двумя чер-
тами в выражении:
а) (157 + 34) - 124 : 62; б) (х + 156) - 143.
361. Запишите сумму:
а) 37 • 2 и 45 - 17; б) 156 : 12 и 31 • 7.
362. По дороге движутся навстречу друг другу пешеход и велосипедист.
Сейчас расстояние между ними 52 км. Скорость пешехода 4 км/ч, а скорость
велосипедиста 9 км/ч. Какое расстояние будет между ними через 1 ч; через
2 ч; через 4 ч? Через сколько часов пешеход и велосипедист встретятся?
363. Найдите значение выражения:
1) 1032 : (5472 : 19 : 12); 2) 15 732 : 57 : (156 : 13).
364. Упростите выражение:
а) 37 + т + 56; в) 49 - 24 - k;
б) п - 45 - 37; г) 35 - t - 18.
365. Упростите выражение и найдите его значение:
а) 315 - р + 185 при р = 148; 213;
б) 427 - I - 167 при I = 59; 260.
366. Мотогонщик преодолел первый участок трассы за 54 с, второй —
за 46 с, а третий — на п с быстрее, чем второй. Сколько времени затратил
мотогонщик на прохождение этих трех участков? Найдите значение по-
лученного выражения, если п = 9; 17; 22.
367. В треугольнике одна сторона 36 см, другая на 4 см меньше, а тре-
тья на х см больше первой стороны. Найдите периметр треугольника. Со-
ставьте выражение для решения задачи и найдите его значение при х = 4
и х = 8.
* 368. Турист на автобусе проехал 40 км, что в 5 раз больше того пути,
который он прошел пешком. Какой общий путь проделал турист?
v 369. От города до села 24 км. Из города вышел человек и идет со ско-
ростью 6 км/ч. Изобразите на шкале расстояний (одно деление шкалы —
1 км) положение пешехода через 1 ч после выхода из города; через 2 ч;
через 3 ч и т. д. Когда он придет в село?
^ 370. Верно или неверно неравенство:
а) 85 678 > 48 - (369 - 78); б) 7508 + 8534 < 26 038?
371. Найдите значение выражения:
а) 36 366-17 366 : (200 - 162);
б) 2 355 264 : 58 + 1 526 112 : 56;
в) 85 408 - 408 • (155 - 99);
г) 417 908 + 6073 • 56 + 627 044.

Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений

_{Планирование математике, материалы по математике 5 класса скачать, учебники онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.