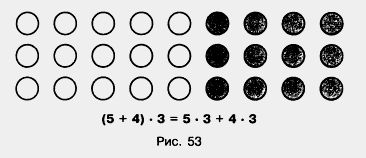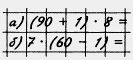Версия 08:09, 16 июня 2010

Гипермаркет знаний>>Математика>>Математика 5 класс>>Математика:Упрощение выражений

                                              Упрощение выражений

Выражения (5 + 4)-З и 5-3 + 4-3 имеют одно и то же значение:

(5 + 4) • 3 = 9 • 3 = 27 и  5 • 3 + 4 • 3 = 15 + 12 = 27.
На рисунке 53 видно, почему эти выражения равны.

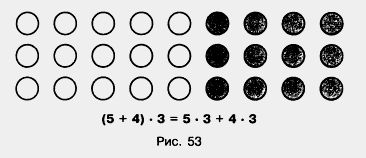
Для того чтобы умножить сумму на чисто, можно умножить на это число каждое слагаемое и сложить получившиеся произведения. Это правило выражает распределительное свойство умножения относительно сложения. С помощью букв его записывают так:
(а + Ь)с = ас + Ьс
Одинаковые значения имеют и выражения (9 - 5) • 3 и 9 • 3 - 5 • 3, так как (9 - 5) • 3 = 4 • 3 = 12 и 9 • 3 - 5 • 3 = 27 - 15 = 12.
Для того чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе.
Это правило называют распределительным свойством умножения относительно вычитания.
С помощью букв его записывают так:
(а - Ь)с = ас - be.
Распределительное свойство умножения позволяет упрощать выражения вида За + la или 26x - 12х.
Имеем: За + 7a = (3 + 7)а = 10а.
Обычно пишут сразу:
За + 7а = 10а (три а да семь а равно десяти а).
26x - 12x = (26- 12)х= 14x.
Обычно пишут сразу:
26х - 12x = 14x (26 икс минус 12 икс равно 14 икс).

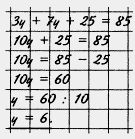
Решим уравнение Зу + 1у + 25 = 85.
Так как Зу + 1у = 10y, то уравнение можно записать так: 10y + 25 = 85. Поэтому 10y = 85 - 25, то есть 10y = 60 и y = 60 : 10.
Итак, у = 6.
Проверка: 3-6 + 7-6 +25 = 85 — верно.
Для упрощения выражений применяют и сочетательное свойство умножения.
Например, выражение 2y • 7 • 10 заменяют на (2 • 7 • 10)y, то есть на 140y.
Пишут:
2y • 7 • 10 = (2 • 7- 10)y = 140y.

Сформулируйте распределительное свойство умножения относительно  сложения и относительно вычитания.
 Поясните, как с помощью этих свойств упрощают выражения вида  8а + 4а, 14x - 9x.

557. Масса чашки 140 г, а масса блюдца 180 г. Купили 12 чашек с блюдцами. Сколько весит эта покупка? На сколько купленные чашки легче
купленных блюдец?

558. За 1 ч работы двигатель расходует 8 л дизельного топлива. До полудня двигатель работал 5 ч, а после полудня 3 ч. Сколько литров дизельного топлива израсходовали за все это время? На сколько больше израсходовали топлива в первой половине дня, чем во второй?

559. Найдите значение произведения с помощью распределительного свойства умножения:

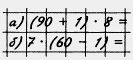
а) 91 • 8;                г) 198 • 4;
б) 7 • 59 ;               д) 202 • 3;
в) 6 • 52;                е) 397 • 5;

ж)24 • 11;
з) 35 • 12;
и) 4 • 505;
к) 25 • 399.

560. Найдите значение выражения:

а) 69 • 27 + 31 • 27;                 г) 263
б) 202 • 87 - 102 • 87;              д) 438
в) 977 • 49 + 49 • 23;               е) 603

561. Примените распределительное свойство умножения:

а) (68 + а) • 2;                      в) 17(14 - х);
б) (b - 7) • 5;                         г) 13(2 + у).

562. При каких значениях х верно равенство:

а) 3(х + 5) = Зх + 15;                    г) (х + 2) • 4 = 2 • 4 + 2
б) (3 + b)х = Зх + 5х;                    д) (5 - 3)х = 5х - Зх;
в) (7 + х) • 5 = 7 • 5 + 8 • 5;           е) (5 - 3)х =bх - 3 • 2?

563. Представьте в виде произведения выражение:

а) 23а + 37а;                   в) 48x + х;               д) 27р - 17р;                ж) 32l - l;
б) 4у + 26у;                    г) у 4- 56y;               е) 84b - 80b;                 з) 1000k - k.

564. Пусть цена 1 кг муки а р., а цена 1 кг сахара Ъ р. Что означает выражение:

а) 9а + 9b;                  б) 9(а + b);              в) 10b - 10а?

565. Расстояние между двумя селами 18 км. Из них выехали в противоположные стороны два велосипедиста. Один проезжает в час т км, а другой — п км. Какое расстояние будет между ними через 4 ч?

566. Найдите значение выражения:

а) 38а + 62а при а = 238; 489;

б) 375b - 175b при b = 48; 517.

567. Найдите значение выражения:

а) 32x + 32y, если х = 4, у = 26;
б) 11m - 11n, если m = 308, n = 208.

568. Решите уравнение:

а) 4х + 4х = 424;                            в) 9z -z = 500;                  д) 4l + 5l + l = 1200
б) 15y - 8у = 714;                           г) 10k - k = 702;                е) 6t + 3t +t = 6400

569. Найдите, при каком значении буквы:

а) выражение 7х больше 4х на 51;
б) выражение 6р меньше 23p? на 102;
в) сумма 8а и За равна 4466;
г) разность 25с и 5с равна 6060.

570. Запишите предложение в виде равенства и выясните, при каких значениях буквы это равенство верно:

а) сумма Зх и bх равна 96;
б) разность 11у и 2у равна 99;
в) Зz больше, чем z, на 48;

г) 27m на 12 меньше, чем 201;
д) 8n вдвое меньше, чем 208;
е) 380 в 19 раз больше 10р.

571. Составьте по рисунку 54 уравнение и решите его.

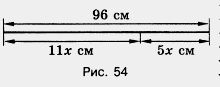
572. Чему равны стороны прямоугольника на рисунке 55, если его периметр равен 240 см?

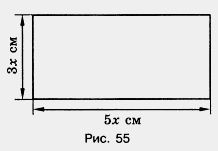
573. Упростите выражение:
а) За + 17 + За + 14;
б) ft + 35 4- 4ft + 26.
574. Решите уравнение:
а) Зх 4- 7х + 18 = 178;
б) 6у - 2у + 25 = 65;
в) lz + 62 - 13 = 130; ' Ъх см
г) 21* - At ~ 17 = 17. Рис. 55
г) 27т на 12 меньше, чем 201;
д) 8п вдвое меньше, чем 208;
е) 380 в 19 раз больше Юр.
96 см
11л: см
Рис. 54
Ъх см
со
87
575. Упростите выражение:
а) 6 • 3 • k; б)8-р-21;
576. Решите уравнение:
а) 4 • 25 • х = 800;
б) у • 5 • 20 = 500;
в) г- 14 • 17.
Я,
Ух
5х
X
X
</х
0*
ti
с*нь
иле
+.
=
= /
— /
=
вей
с,
fta
< -
70
0 :
У
56
56
саа
X
71
5
с.
is
:.
)
в) 21 • 8 • р = 168;
г) т • 3 • 33 = 990.
577. Я задумал число. Если его увеличить на 15, а результат умно-
жить на 8, то получится 160. Какое число я задумал?
578. В книге напечатаны рассказ и повесть, которые
вместе занимают 70 страниц. Повесть занимает в 4 раза
больше страниц, чем рассказ. Сколько страниц занимает
рассказ и сколько повесть?
Решение. Пусть рассказ занимает х страниц, тогда
повесть занимает 4# страниц. По условию задачи, рас-
сказ и повесть вместе занимают 70 страниц. Получаем
уравнение: 4х + х = 70. Отсюда Ъх = 70, х = 70 : 5,
х = 14. Значит, рассказ занимает 14 страниц, а повесть —
56 страниц (14 • 4 = 56).
Проверка корня уравнения: 14 + 56 = 70.
579. На уборке картофеля собрали 1650 кг за день.
После обеда собрали в 2 раза меньше, чем до обеда.
Сколько картофеля собрали после обеда?
580. Для школы купили 220 столов и стульев, причем стульев — в 9 раз
больше, чем столов. Сколько столов и сколько стульев купили?
581. Площадь кухни в 3 раза меньше площади комнаты, поэтому для
ремонта пола кухни потребовалось на 24 м2 линолеума меньше, чем для
комнаты. Какова площадь кухни?
582. Точка М делит отрезок АВ на два отрезка: AM и MB. Отрезок AM
длиннее отрезка MB в 5 раз, а отрезок MB короче отрезка AM на 24 мм.
Найдите длину отрезка AM, длину отрезка MB и
длину отрезка АВ.
583. Для приготовления напитка берут 2 части
вишневого сиропа и 5 частей воды. Сколько надо
взять сиропа, чтобы получить 700 г напитка?
Решение. Пусть масса одной части напитка
х г. Тогда масса сиропа 2х г, а масса напитка
{2х + Ъх) г. По условию задачи масса напитка
равна 700 г. Получим уравнение: 2х + Ъх = 700.
Отсюда 7х = 700, х = 700 : 7 и х = 100, то есть масса
одной части равна 100 г. Поэтому сиропа надо взять
200 г (100 • 2 = 200) и воды 500 г (100 • 5 = 500).
Проверка: 200 + 500 = 700.
я,
oqn
&4
Во,
2х
7х
х '■
0*
ой
юн
+ .
=
мс
г
5.
5х
70L
00.
: 4
сса
Ни
: г
: i
=: /
2х
00
к г
00
=
г с
20
l/Wl
л
с/ t
9.
\а.
88
584. При помоле ржи получается б частей муки и 2 части отрубей.
Сколько получится муки, если смолоть 1 т ржи?
585. Чтобы приготовить состав для полировки медных изделий, берут
10 частей воды, 5 частей нашатырного спирта и 2 части мела (по массе).
Сколько граммов каждого вещества надо взять, чтобы приготовить 340 г
состава?
586. Для приготовления бутылочного стекла берут 25 частей песка,
9 частей соды и 5 частей извести (по массе). Сколько потребуется соды,
чтобы изготовить 390 кг стекла?
587. Мороженое содержит 7 частей воды, 2 части молочного жира и
2 части сахара (по массе). Сколько потребуется сахара для приготовления
4400 кг мороженого?
\ 588. На одной стороне улицы вдвое больше домов, чем на другой. Ко-
\гда на улице построили еще 12 домов, то всего стало 99 домов. Сколько
домов было на каждой стороне улицы?
589. По числовому равенству 3-12 + 4- 12+- 15- 12 = 264 составьте
уравнение, имеющее корень 12 и содержащее три раза букву х. Приду-
майте задачу по этому уравнению.
590. Вычислите устно: JTT
а) 100-55 б) 90-71 в) 100-54 г) 100-13
• 2 -3 : 23 : 3
: 18 +23 -19 +27
• 15 : 16 +22 : 14
591. Найдите значение выражения наиболее удобным способом:
а) 125 -23-8; б) 11 • 16 • 125; в) 19 + 78 + 845 + 81 + 155.
592. Найдите корень уравнения:
а) 45 = 45 + у\ в) у - 45 = 45;
б) 45 - у = 45; г) 0 = 45 - х.
593. Угадайте корни уравнения:
а) х- 197 = 2945 - 197;
б) у : 89 = 1068 : 89;
в) 365а = 53 ■ 365.
594. Придумайте задачу по уравнению:
а) За + 2а = 75;
б) с + с + с = 46 + с;
в) т + 5т = 90.
89
595. При сложении каких чисел может получиться 0? Подумайте, в каких
случаях получится число 0 при вычитании, при умножении, при делении.
596. Сумма пяти натуральных чисел равна произведению этих чисел.
Какие это числа?
597. Саша любит решать трудные задачи. Он рассказал, что за 4 дня смог
решить 23 задачи. В каждый следующий день он решал больше задач, чем в
предыдущий, и в четвертый день решил вчетверо больше, чем в первый.
Сколько задач решил Саша в каждый из этих четырех дней?
598. Код для открывания сейфа состоит из четырех цифр. Сколько суще-
ствует различных вариантов кода для этого сейфа?
599. Выполните деление с остатком:
978 : 13; 780 : 24; 4295 : 126.
600. Найдите делимое, если неполное частное 25, делитель 8, остаток 5.
601. Решите уравнение:
а) х : 16 = 324 + 284;
б) 1344 : у = 543 - 487;
в) z • 49 = 927 + 935;
Рис. 56
2х см
Зх см
г) (3724 + р) : 54 = 69;
д) 992 : (130- k) = 8;
е) (148- т) • 31 = 1581.
602. По рисунку 56 составьте
уравнение и найдите массу каждо-
го батона. (Масса гирь дана в ки-
лограммах.)
603. По рисунку 57 найдите
длину отрезка ВС, если AD = 40 см.
Ъх см
В
С
Рис. 57
D
604. Периметр треугольника ABC равен 64 см, сторона АВ меньше сторо-
ны АС на 7 см, но больше стороны ВС на 12 см. Найдите длину каждой сто-
роны треугольника ABC.
605. В соревнованиях по стрельбе участвовали 12 человек. Сколько пат-
ронов получил каждый участник, если потребовалось 8 коробок, по 30 патро-
нов в каждой?
606. Три заготовителя собрали 240 кг лекарственных трав. Первый собрал
87 кг, а первый и второй вместе — 174 кг. Сколько килограммов лекарствен-
ных трав собрал второй заготовитель и сколько третий?
90
607. Решите задачу:
1) Велосипедист ехал 2 ч с некоторой скоростью. После того как он про-
едет еще 4 км, его путь станет равным 30 км. С какой скоростью ехал вело-
сипедист?
2) Мотоциклист ехал 3 ч с некоторой скоростью. Если он проедет еще 12 км,
то его путь станет равен 132 км. С какой скоростью ехал мотоциклист?
(3) В мешке 20 кг крупы. После того как крупой наполнили несколько паке-
тов по 3 кг, в мешке осталось 5 кг. Сколько пакетов наполнили крупой?
4) В бидоне 39 л молока. После того как молоком наполнили несколько
двухлитровых банок, в бидоне осталось 7 л. Сколько банок наполнили?
608. Найдите значение выражения:
1) 47 040 : 14:7 : 32; 3) 46 • 9520 : 68 : 7;
2) 101 376 : 48 : 24 : 8; 4) 319 488 : 96 : 64 • 23.
609. Примените распределительное свойство умножения: 9[
а) 11 • (60 + а); в) (х - 9) • 24; А
б) 21 • (38 - Ь); г) (у + 4) • 38.
610. Найдите значение выражения, применив распределительное свой-
ство умножения:
а) (250 + 25) • 4; в) 8 • 11 + 8 • 29;
б) 6 • (150 + 16); г) 36 • 184 + 36 • 816.
611. Найдите значение выражения:
а) (30 - 2) • 5; в) 85 • 137 - 75 • 137;
б) 7 • (60 - 2); г) 78 • 214 - 78 • 204.
612. Упростите выражение:
а) 4а + 90а; б) 86Ь - ПЬ; в) 209т + т; г) 302п - п.
613. Найдите значение выражения:
а) 24а + 47а + 53а + 76а, если а = 47;
б) 128р - 72р - 28р, если р = 11.
614. Решите уравнение:
а) 14* + 27* = 656; в) 492 - г = 384;
б) 81у - 38у = 645; г) 102/г - 4й = 1960.
615. При каком значении z сумма 5z и 15z равна 840?
616. Масса одного метра рельса равна 32 кг. Сколько понадобится же-
лезнодорожных вагонов грузоподъемностью 60 т, чтобы перевезти все рель-
сы, необходимые для постройки одноколейной железной дороги длиной
180 км?
617. В бидоне 36 л молока. Когда из него перелили в другой бидон 4 л,
в обоих бидонах молока стало поровну. Сколько литров молока было в
другом бидоне?
91
618. В двух карманах было 28 орехов, причем в левом кармане в
3 раза больше, чем в правом. Сколько орехов было в каждом кармане?
619. Площадь физкультурного зала в 6 раз больше площади классной
комнаты. Найдите площадь зала, если она больше площади классной ком-
наты на 250 м2.
620. На складе всего 88 л сока; трехлитровых банок апельсинового сока
столько же, сколько пятилитровых банок яблочного сока. Сколько лит-
ров апельсинового сока на складе?
621. Чтобы сделать казеиновый клей, берут 11 частей воды, 5 частей
нашатырного спирта и 4 части казеина (по массе). Сколько получится ка-
зеинового клея, если на него будет израсходовано нашатырного спирта на
60 г меньше, чем воды?
622. Для приготовления вишневого варенья на 2 части вишни берут
3 части сахара (по массе). Сколько вишни и сколько сахара пошло на ва-
ренье, если сахара пошло на 7 кг 600 г больше, чем вишни?
щ
/Зи
Са
(4UC
ну
г
гса
2х
1х
г б
^ >
Ъ
и ч
асл
ие
lU .
на
г г
7а
г 6
00
i
623. С двух яблонь собрали 67 кг яблок, причем с одной яблони собра-
ли на 19 кг больше, чем с другой. Сколько килограммов яблок собрали с
каждой яблони?
/
2
■А .
■Л .
г£л.
ОНА
ОНА
и
(*
X А
<а*
+
г
ЩХ1
ad
) JC
OK
67
кг
624. Из 523 цыплят, выведенных в инкубаторе, петушков оказалось
на 25 меньше, чем курочек. Сколько курочек и сколько петушков было
выведено в инкубаторе?
625. Найдите значение выражения:
а) 5007 • (11 815 : 85 - (4806 - 4715));
б) 6003 • (24 396 : 76 - 319 + 26);
в) 213 213 : (403 -36-14 469);
г) 7866 : 38 - 16 146 : 78.
626. Разгадайте чайнворд, помещенный на форзаце в конце учебника.

Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений

_{Календарно-тематическое планирование, задачи школьнику 5 класса по математике скачать, Математика онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.