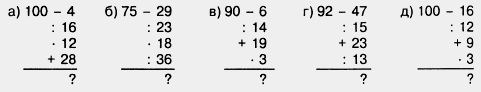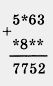Версия 09:48, 16 июня 2010

Гипермаркет знаний>>Математика>>Математика 5 класс>>Математика:Степень числа. Квадрат и куб числа

                                                       Степень числа. Квадрат и куб числа

Мы знаем, что сумму, в которой все слагаемые равны друг другу, можно записать короче — в виде произведения. Например, вместо 3 + 3 + 3 + 3 + 3
пишут 3 • 5. В этом произведении число 5 показывает, сколько слагаемых было в сумме.
Произведение, в котором все множители равны друг другу, тоже записывают короче: вместо 2 • 2 • 2 • 2 • 2 • 2 пишут 26. Запись 26 читают: «два в шестой степени». В этой записи число 2 называют основанием степени, число 6, которое показывает, сколько множителей было в произведении, — показателем степени, а выражение 26 называют степенью.

Пример 1. Запишем произведения в виде степени и найдем их значения:

3 • 3 • 3 • 3 = 34 = 81;
5 . 5 • 5 = 53= 125;
2 • 2 • 2 • 2 • 2 • 2 = 26 = 64.

торую степень числа часто называют иначе. Произведение 3 • 3 называют квадратом числа 3 и обозначают З².
Произведение n и n называют квадратом числа n и обозначают n2 (читают: «эн в квадрате»). Итак, n² = n • n.

Например, 172 = 17 • 17 = 289.

Таблица квадратов первых 10 натуральных чисел имеет следующий вид:

Третья степень числа также имеет и иное название. Произведение 4 • 4 • 4 называют кубом числа 4 и обозначают 4³. Произведение n • n • n называют кубом числа n и обозначают n³ (читают: 5 «эн в кубе»).
Итак, n³ = n • n • n.
Например, 8³ = 8 •8 •8 = 64-8 = 512.

Таблица кубов первых 10 натуральных чисел имеет вид:

Первую степень числа считают равной самому числу:
                                            7¹ = 7, 16¹ = 16, 1¹ = 1.
Показатель степени 1 обычно не пишут.
Если в числовое выражение входят степени чисел, то их значения вычисляют до выполнения остальных действий.

Пример 2. Найдем значение выражения (4 + З)² • 5² - 8³ + 2⁶.
Решение.

(4 + З)² • 5² - 8³ + 2⁶ = 7² - 25 - 512 + 64= 49 • 25 - 512 + 64 = 1225 - 512 + 64 = 777.

Что такое квадрат числа?
Что такое куб числа?
Назовите основание и показатель степени: б7, 123, 410, 152, 81.

652. Составьте таблицу квадратов чисел от 11 до 20.

653. Представьте в виде степени произведение:

а) 6 • 6 • 6 • 6 • 6 • 6 • 6;                                            
в) 73 • 73;                                        

б) 25 • 25 • 25 • 25 • 25;                                                  
г) 11 • 11 • 11 • 11;
д) 9 • 9 • 9;
е)  m• m • m • m • m • m;

ж) х • х • х;

з) у• у •у• у• у• у• у •у;

и) k • к

к) n • n • n •n • n;

л) (х + 1)(х + 1)(х + 1);

м) (7 - n)(7 - n).

654. Представьте в виде произведения степень:

а) 7⁵;                        г) 1000²;                 ж) k³;                  к) (m + 2)⁴;
б) 12⁴;                      д) 60⁷;                     з) а⁸;                  л) (а - 7)²;
в) 15³;                      е) n⁹;                       и) х²;                  м) (х 4- у)³.

655. Найдите значения: 252; 1002; 103; II3; 123; 153.

656. Найдите значения степеней: 25; 106; I20; З4; 411; 44.

657. Найдите значение выражения:

а) З² • 18;                      д) 7 + 4³;                       и) 5² • 2³;
б) 5 + 4²;                       е) 7³ + 4;                       к) 2⁵ + З⁴;
в) (5 + 4)²;                     ж) (7 + 4)³;                     л) (30 : З)⁵ - 100³;
г) 5² + 4²;                      з) (7³ - 4³) : (7 - 4);         м) (10² - 2⁶) : 6 + 1¹⁰.

658. Пользуясь таблицами квадратов и кубов чисел, найдите значение д, если:

121 - n²; n² = 196; n² = 10 000; 125 = n³; n³ = 512.

659. Вычислите устно:

660. Угадайте корни уравнения:

а) х • х = 25;                    в) а • а = 1;
б) у • у = 81;                      г)Ь•Ь•Ь = 0.

661. Какие цифры заменены звездочками?

Подумайте, какие уравнения пришлось решать для нахождения 7752 неизвестных цифр.

662. Каков порядок выполнения действий при вычислении значения выражения:

а) 160 + 37 - 20;

б) 90 - 60 : 15;

в) 80 - 15 + 25?

Если возможно, укажите другой порядок действий, приводящий к тому же результату.

663. Составьте выражение по следующей программе:

1. Разделить 58 344 на 429.
2. 215 умножить на 48.
3. Сложить результаты команд 1 и 2.
Найдите значение получившегося выражения.

664. Составьте схему вычисления выражения:

(39 • 71 + 25 • 95) - (248 : 4 - 176 : 11).

665. Решите задачу:
1) Сумма двух чисел 549. Одно из них в 8 раз больше другого. Найдите эти числа.
2) Сумма двух чисел 378. Одно из них в 8 раз меньше другого. Найдите эти числа.
3) Разность двух чисел 342. Одно из них в 7 раз меньше другого. Найдите эти числа.
4) Разность двух чисел 516. Одно из них в 7 раз больше другого. Найдите эти числа.

666. Найдите значения:

18²; 53; 13²; 20³; 40²; 30³.

667. Найдите значения: 2⁴; З³; 10⁵; 1¹²; 100⁴; 20⁶.

668. Найдите значение выражения:

а) 9² + 19;                  е) (17 - 16)⁸ + 2⁵;
б) 17² - 209;               ж) 10⁶ - 20⁴;
в) б³ : 3;                     з) З⁴ • 10⁴;
г) 2³ • З²;                   и) 5⁴ : 5².
д) (15 - 7)² : 2³;

669. Из Москвы и Ростова-на-Дону одновременно вышли навстречу друг другу два поезда. Поезд из Москвы шел со скоростью 65 км/ч, а поезд из Ростова-на-Дону — со скоростью на 7 км/ч меньшей. На каком расстоянии друг от друга будут поезда через 6 ч после начала движения, если расстояние между Москвой и Ростовом-на-Дону 1230 км?

670. С двух станций, расстояние между которыми 720 км, вышли одновременно навстречу друг другу два поезда. Скорость первого поезда 75 км/ч, а скорость второго на 10 км/ч больше. На каком расстоянии друг от друга будут поезда через 4 ч?

671. Составьте программу вычислений для нахождения значения выражения

               67 392 : (3504 - 3408) + 19 232 : 601
и изобразите ее схемой. Найдите значение выражения.

672. Выполните действия:

                     14 • (3600 • 18 - 239 200 : 46).


Выдающийся российский математик академик Андреи Николаевич Колмогоров решил много сложнейших задач, совершил не одно открытие в различных разделах современной математики. Но радость своих первых математических «открытий» он познал рано. Андрей Николаевич рассказывал, что еще до поступления в гимназию в возрасте пяти-шести лет он любил придумывать задачи, подмечал интересные свойства чисел. Эти «открытия» публиковались в домашнем журнале. Вот одно из «открытий» шестилетнего Колмогорова. Он заметил, что

1² = 1,           2² = 1+3,             3² = 1+3 + 5,           4² = 1+3 + 5 + 7.

 673. Попробуйте рассказать, что это за свойство. Проверьте, выполняется ли оно для квадратов нескольких следующих чисел,

Первые единицы длины как в России, так и в других странах были связаны с размерами частей тела человека. Таковы сажень, локоть, пядь. В Англии и США до сих пор используется «ступня» — фут (31 см), «большой палеи,» — дюйм (25 мм) и даже ярд (91 см) — единица длины, появившаяся почти 900 лет назад.
Она была равна расстоянию от кончика носа короля Генриха I до конца пальцев его вытянутой руки.
Для измерения больших расстояний на Руси использовали единииу пoприще, замененную позже верстбй (в разных местностях версту считали по-разному — от 500 до 750 сажен).
От восточных купцов пошла единица аршин (тоже означает «локоть») — существовали турецкий аршин, персидский аршин и др. Поэтому и возникла по-
говорка «мерить на свой аршин».
Множество единиц существовало и для измерения массы. Наиболее древняя русская мера — гривна, или гривенка (около 410 г). Позднее появились золотники, фунты, пуды.
В связи с развитием торговли назрела необходимость установить четкие определения единиц и соотношения между ними. При Петре I русские меры были
приведены в определенную систему:

1 верста = 500 саженям (1 км 67 м);
1 сажень = 3 аршинам (2131см);
1 аршин = 16 вершкам = 28 дюймам (71 см);
1 фут = 12 дюймам (30 см 5 мм):
1 пуд = 40 фунтам (гривенкам) (16 кг 400 г);
1 фунт = 96 золотникам (410 г).

Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений

_{Книги и учебники согласно календарному плануванння по математике 5 класса скачать, помощь школьнику онлайн}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.