|
|
|
| Строка 1: |
Строка 1: |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Рациональные неравенства<metakeywords>Рациональные неравенства</metakeywords>''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Рациональные неравенства<metakeywords>Рациональные неравенства</metakeywords>''' |
| | + | |
| | + | <br> |
| | + | |
| | + | '''РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА'''<br><br>Рациональное неравенство с одной переменной х — это неравенство вида [[Image:a921.jpg]] рациональные выражения, т.е. алгебраические выражения, составленные из чисел и переменной х с помощью операций сложения, вычитания, умёо-жения, деления и возведения в натуральную степень. Разумеется, переменная может быть обозначена любой другой буквой, но в математике чаще всего предпочтение отдается букве х.[[Image:]]<br>При решении рациональных неравенств используются те три правила, которые были сформулированы выше в § 1. С помощью этих правил обычно преобразуют заданное рациональное неравенство к виду [[Image:a922.jpg]] — алгебраическая дробь (или многочлен). Далее разлагают числитель и знаменатель дроби f / (х) на множители вида х - а (если, конечно, это возможно) и применяют метод интервалов, который мы уже упоминали выше (см. в предыдущем параграфе пример 3).<br><br>'''Пример 1'''. |
| | + | |
| | + | [[Image:a923.jpg]]<br><br><br>'''Пример 2.''' |
| | + | [[Image:a924.jpg]]<br><br>'''П р и м е р 3.''' |
| | + | |
| | + | [[Image:a925.jpg]]<br><br>'''Пример 4.''' |
| | + | |
| | + | [[Image:a926.jpg]]<br><br><br>При этом количество множителей в числителе и знаменателе дроби может быть любым. Затем отмечали на числовой прямой точки а,Ь,с,д. и определяли знаки выражения fх) на выделенных промежутках. Заметили, что на самом правом из выделенных промежутков выполняется неравенство fх) > 0, а далее по промежуткам знаки выражения fх) чередуются (см. рис. 16а). Это чередование удобно иллюстрировать с помощью волнообразной кривой, которая чертится справа налево и сверху вниз (рис. 166). На тех промежутках, где эта кривая (ее иногда называют кривой знаков) расположена выше оси х, выполняется неравенство fх) > 0; где эта кривая расположена ниже оси х, выполняется неравенство fх) < 0.<br>[[Image:a927.jpg]]<br><br>'''Пример 5.''' |
| | + | |
| | + | [[Image:a928.jpg]]<br><br><br>Обращаем ваше внимание на то, что встречаются рациональные неравенства, при решении которых метод интервалов следует применять с осторожностью, с некоторыми поправками. Эту мысль мы обсудим в остальных примерах параграфа.<br><br>'''Пример 6.''' |
| | + | |
| | + | [[Image:a929.jpg]]<br><br>'''Пример 7.''' |
| | + | |
| | + | [[Image:a9210.jpg]]<br><br>'''Пример 8.''' |
| | + | |
| | + | '''[[Image:a9211.jpg]]''' |
| | + | <br> |
| | + | |
| | | | |
| | А.Г. Мордкович Алгебра 9 класс | | А.Г. Мордкович Алгебра 9 класс |
| Строка 55: |
Строка 76: |
| | </u> | | </u> |
| | | | |
| - | | + | <br> |
| | | | |
| | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам]. | | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам]. |
| | | | |
| | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум]. | | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум]. |
Версия 10:07, 20 июня 2010
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика:Рациональные неравенства
РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА
Рациональное неравенство с одной переменной х — это неравенство вида 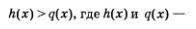 рациональные выражения, т.е. алгебраические выражения, составленные из чисел и переменной х с помощью операций сложения, вычитания, умёо-жения, деления и возведения в натуральную степень. Разумеется, переменная может быть обозначена любой другой буквой, но в математике чаще всего предпочтение отдается букве х.[[Image:]] рациональные выражения, т.е. алгебраические выражения, составленные из чисел и переменной х с помощью операций сложения, вычитания, умёо-жения, деления и возведения в натуральную степень. Разумеется, переменная может быть обозначена любой другой буквой, но в математике чаще всего предпочтение отдается букве х.[[Image:]]
При решении рациональных неравенств используются те три правила, которые были сформулированы выше в § 1. С помощью этих правил обычно преобразуют заданное рациональное неравенство к виду 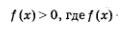 — алгебраическая дробь (или многочлен). Далее разлагают числитель и знаменатель дроби f / (х) на множители вида х - а (если, конечно, это возможно) и применяют метод интервалов, который мы уже упоминали выше (см. в предыдущем параграфе пример 3). — алгебраическая дробь (или многочлен). Далее разлагают числитель и знаменатель дроби f / (х) на множители вида х - а (если, конечно, это возможно) и применяют метод интервалов, который мы уже упоминали выше (см. в предыдущем параграфе пример 3).
Пример 1.

Пример 2.

П р и м е р 3.

Пример 4.

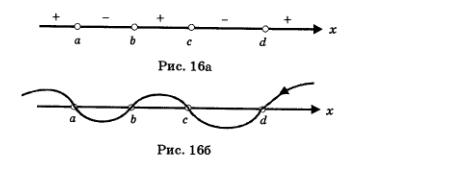
При этом количество множителей в числителе и знаменателе дроби может быть любым. Затем отмечали на числовой прямой точки а,Ь,с,д. и определяли знаки выражения fх) на выделенных промежутках. Заметили, что на самом правом из выделенных промежутков выполняется неравенство fх) > 0, а далее по промежуткам знаки выражения fх) чередуются (см. рис. 16а). Это чередование удобно иллюстрировать с помощью волнообразной кривой, которая чертится справа налево и сверху вниз (рис. 166). На тех промежутках, где эта кривая (ее иногда называют кривой знаков) расположена выше оси х, выполняется неравенство fх) > 0; где эта кривая расположена ниже оси х, выполняется неравенство fх) < 0.
Пример 5.

Обращаем ваше внимание на то, что встречаются рациональные неравенства, при решении которых метод интервалов следует применять с осторожностью, с некоторыми поправками. Эту мысль мы обсудим в остальных примерах параграфа.
Пример 6.

Пример 7.

Пример 8.
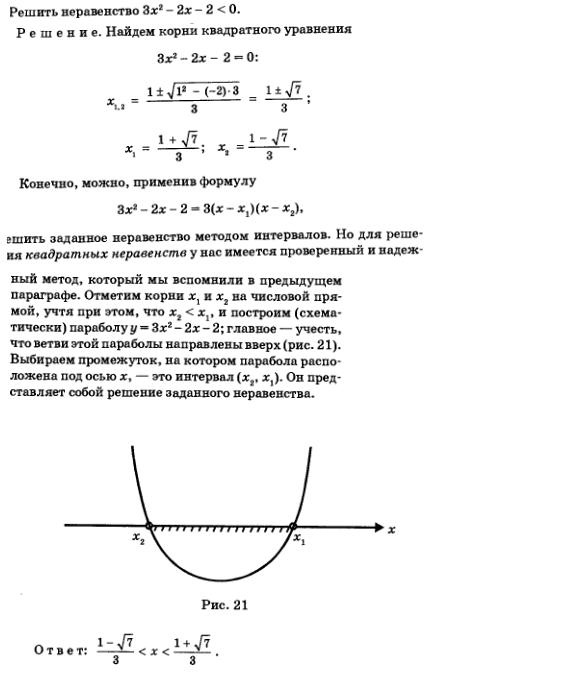
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|



















