Трапеция — Гипермаркет знаний

KNOWLEDGE HYPERMARKET

Трапеция

 		Версия 06:56, 22 июня 2010 (просмотреть исходный код)
User16  (Обсуждение | вклад)
 (Создана новая страница размером <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, ...)
← Предыдущая правка
		Версия 06:56, 22 июня 2010 (просмотреть исходный код)
User16  (Обсуждение | вклад) 
Следующая правка →
		
Строка 5:
Строка 5:
 <br>    <br>  
  
- '''&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp; ТРАПЕЦИЯ''' + '''&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp; ТРАПЕЦИЯ'''  
  
- <br>'''''Трапецией называется четырехугольник, у которого только две противолежащие стороны параллельны. Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами.''''' + <br>'''''Трапецией называется четырехугольник, у которого только две противолежащие стороны параллельны. Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами.'''''  
  
- На рисунке 135 вы видите трапецию ABCD с основаниями АВ и CD и боковыми сторонами ВС и AD. + На рисунке 135 вы видите трапецию ABCD с основаниями АВ и CD и боковыми сторонами ВС и AD.  
  
- '''''Трапеция, у которой боковые стороны равны, называется равнобокой. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.''''' + '''''Трапеция, у которой боковые стороны равны, называется равнобокой. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.'''''  
  
  + <br> 
  
  + [[Image:22-06-16.jpg]]<br><br>Теорема 6.8. '''''Средняя линия трапеции параллельна основаниям и равна их полусумме.''''' 
  
- [[Image:22-06-16.jpg]]<br><br>Теорема 6.8. '''''Средняя линия трапеции параллельна основаниям и равна их полусумме.''''' + Доказательство. Пусть ABCD — данная трапеция (рис. 136). Проведем через вершину В и середину Р боковой стороны CD прямую. Она пересекает прямую AD в некоторой точке Е.  
  
- Доказательство. Пусть ABCD — данная трапеция (рис. 136). Проведем через вершину В и середину Р боковой стороны CD прямую. Она пересекает прямую AD в некоторой точке Е. + Треугольники РВС и PED равны по второму признаку равенства треугольников. У них CP=DP по построению, углы при вершине Р равны как вертикальные, а углы РСВ и PDE равны как внутренние накрест лежащие при параллельных прямых ВС и AD и секущей CD. Из равенства треугольников следует равенство сторон: РВ=РЕ, BC=ED.  
  
- Треугольники РВС и PED равны по второму признаку равенства треугольников. У них CP=DP по построению, углы при вершине Р равны как вертикальные, а углы РСВ и PDE равны как внутренние накрест лежащие при параллельных прямых ВС и AD и секущей CD. Из равенства треугольников следует равенство сторон: РВ=РЕ, BC=ED. + Значит, средняя линия PQ трапеции является средней линией треугольника ABE. По свойству средней линии треугольника PQIIAE и отрезок 
  
- Значит, средняя линия PQ трапеции является средней линией треугольника ABE. По свойству средней линии треугольника PQIIAE и отрезок + [[Image:22-06-17.jpg]]<br><br>Теорема доказана.  
  
- [[Image:22-06-17.jpg]]<br><br>Теорема доказана. + Задача (60). Докажите, что у равнобокой трапеции углы при основании равны.  
  
- Задача (60). Докажите, что у равнобокой трапеции углы при основании равны. + Решение. Пусть ABCD — равнобокая трапеция (рис. 137). Докажем, что углы трапеции при основании CD равны.<br><br>[[Image:22-06-18.jpg]]<br>&nbsp;<br>Проведем через вершину В прямую, параллельную стороне AD. Она пересечет луч DC в некоторой точке Е. Четырехугольник ABED — параллелограмм. По свойству параллелограмма BE=AD. По условию AD=BC (трапеция равнобокая), значит, треугольник ВСЕ равнобедренный с основанием ЕС. Углы треугольника и трапеции при вершине С совпадают, а углы при вершинах Е и D равны как соответственные углы при пересечении параллельных прямых секущей. Поэтому [[Image:20-06-61.jpg]]ADC= [[Image:20-06-61.jpg]]BCD. Утверждение доказано.<br>&nbsp;  
-   + 
- Решение. Пусть ABCD — равнобокая трапеция (рис. 137). Докажем, что углы трапеции при основании CD равны.<br><br>[[Image:22-06-18.jpg]]<br>&nbsp;<br>Проведем через вершину В прямую, параллельную стороне AD. Она пересечет луч DC в некоторой точке Е. Четырехугольник ABED — параллелограмм. По свойству параллелограмма BE=AD. По условию AD=BC (трапеция равнобокая), значит, треугольник ВСЕ равнобедренный с основанием ЕС. Углы треугольника и трапеции при вершине С совпадают, а углы при вершинах Е и D равны как соответственные углы при пересечении параллельных прямых секущей. Поэтому [[Image:20-06-61.jpg]]ADC= [[Image:20-06-61.jpg]]BCD. Утверждение доказано.<br>&nbsp; + 
  
 <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>    <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>  
  
- <sub>Видео по математике[[Математика|скачать]], домашнее задание, учителям и школьникам на помощь [[Гипермаркет знаний - первый в мире!|онлайн]]</sub>   + <sub>Видео по математике [[Математика|скачать]], домашнее задание, учителям и школьникам на помощь [[Гипермаркет знаний - первый в мире!|онлайн]]</sub>  
  
 <br>    <br>  

Версия 06:56, 22 июня 2010
 
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Трапеция 

 
                                                             ТРАПЕЦИЯ 

Трапецией называется четырехугольник, у которого только две противолежащие стороны параллельны. Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами. 
На рисунке 135 вы видите трапецию ABCD с основаниями АВ и CD и боковыми сторонами ВС и AD. 
Трапеция, у которой боковые стороны равны, называется равнобокой. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции. 

 


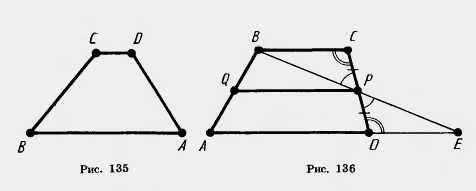
Теорема 6.8. Средняя линия трапеции параллельна основаниям и равна их полусумме. 
Доказательство. Пусть ABCD — данная трапеция (рис. 136). Проведем через вершину В и середину Р боковой стороны CD прямую. Она пересекает прямую AD в некоторой точке Е. 
Треугольники РВС и PED равны по второму признаку равенства треугольников. У них CP=DP по построению, углы при вершине Р равны как вертикальные, а углы РСВ и PDE равны как внутренние накрест лежащие при параллельных прямых ВС и AD и секущей CD. Из равенства треугольников следует равенство сторон: РВ=РЕ, BC=ED. 
Значит, средняя линия PQ трапеции является средней линией треугольника ABE. По свойству средней линии треугольника PQIIAE и отрезок 


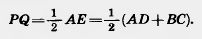
Теорема доказана. 
Задача (60). Докажите, что у равнобокой трапеции углы при основании равны. 
Решение. Пусть ABCD — равнобокая трапеция (рис. 137). Докажем, что углы трапеции при основании CD равны.


 
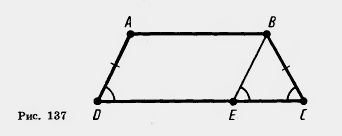
Проведем через вершину В прямую, параллельную стороне AD. Она пересечет луч DC в некоторой точке Е. Четырехугольник ABED — параллелограмм. По свойству параллелограмма BE=AD. По условию AD=BC (трапеция равнобокая), значит, треугольник ВСЕ равнобедренный с основанием ЕС. Углы треугольника и трапеции при вершине С совпадают, а углы при вершинах Е и D равны как соответственные углы при пересечении параллельных прямых секущей. Поэтому ADC= BCD. Утверждение доказано.
  

 А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений 
 
_{Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн} 

 

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников
 
Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 
 
Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки



 
Если у вас есть исправления или предложения к данному уроку, напишите нам. 
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.

Источник — «http://edufuture.biz/index.php?title=%D0%A2%D1%80%D0%B0%D0%BF%D0%B5%D1%86%D0%B8%D1%8F»
@@ Строка 5: / Строка 5: @@
 <br>
 '''&nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp; ТРАПЕЦИЯ'''
 <br>'''''Трапецией называется четырехугольник, у которого только две противолежащие стороны параллельны. Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами.'''''
 На рисунке 135 вы видите трапецию ABCD с основаниями АВ и CD и боковыми сторонами ВС и AD.
 '''''Трапеция, у которой боковые стороны равны, называется равнобокой. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.'''''
+<br>
+[[Image:22-06-16.jpg]]<br><br>Теорема 6.8. '''''Средняя линия трапеции параллельна основаниям и равна их полусумме.'''''
-[[Image:22-06-16.jpg]]<br><br>Теорема 6.8. '''''Средняя линия трапеции параллельна основаниям и равна их полусумме.'''''
+Доказательство. Пусть ABCD — данная трапеция (рис. 136). Проведем через вершину В и середину Р боковой стороны CD прямую. Она пересекает прямую AD в некоторой точке Е.
-Доказательство. Пусть ABCD — данная трапеция (рис. 136). Проведем через вершину В и середину Р боковой стороны CD прямую. Она пересекает прямую AD в некоторой точке Е.
+Треугольники РВС и PED равны по второму признаку равенства треугольников. У них CP=DP по построению, углы при вершине Р равны как вертикальные, а углы РСВ и PDE равны как внутренние накрест лежащие при параллельных прямых ВС и AD и секущей CD. Из равенства треугольников следует равенство сторон: РВ=РЕ, BC=ED.
-Треугольники РВС и PED равны по второму признаку равенства треугольников. У них CP=DP по построению, углы при вершине Р равны как вертикальные, а углы РСВ и PDE равны как внутренние накрест лежащие при параллельных прямых ВС и AD и секущей CD. Из равенства треугольников следует равенство сторон: РВ=РЕ, BC=ED.
+Значит, средняя линия PQ трапеции является средней линией треугольника ABE. По свойству средней линии треугольника PQIIAE и отрезок
-Значит, средняя линия PQ трапеции является средней линией треугольника ABE. По свойству средней линии треугольника PQIIAE и отрезок
+[[Image:22-06-17.jpg]]<br><br>Теорема доказана.
-[[Image:22-06-17.jpg]]<br><br>Теорема доказана.
+Задача (60). Докажите, что у равнобокой трапеции углы при основании равны.
-Задача (60). Докажите, что у равнобокой трапеции углы при основании равны.
+Решение. Пусть ABCD — равнобокая трапеция (рис. 137). Докажем, что углы трапеции при основании CD равны.<br><br>[[Image:22-06-18.jpg]]<br>&nbsp;<br>Проведем через вершину В прямую, параллельную стороне AD. Она пересечет луч DC в некоторой точке Е. Четырехугольник ABED — параллелограмм. По свойству параллелограмма BE=AD. По условию AD=BC (трапеция равнобокая), значит, треугольник ВСЕ равнобедренный с основанием ЕС. Углы треугольника и трапеции при вершине С совпадают, а углы при вершинах Е и D равны как соответственные углы при пересечении параллельных прямых секущей. Поэтому [[Image:20-06-61.jpg]]ADC= [[Image:20-06-61.jpg]]BCD. Утверждение доказано.<br>&nbsp;
-Решение. Пусть ABCD — равнобокая трапеция (рис. 137). Докажем, что углы трапеции при основании CD равны.<br><br>[[Image:22-06-18.jpg]]<br>&nbsp;<br>Проведем через вершину В прямую, параллельную стороне AD. Она пересечет луч DC в некоторой точке Е. Четырехугольник ABED — параллелограмм. По свойству параллелограмма BE=AD. По условию AD=BC (трапеция равнобокая), значит, треугольник ВСЕ равнобедренный с основанием ЕС. Углы треугольника и трапеции при вершине С совпадают, а углы при вершинах Е и D равны как соответственные углы при пересечении параллельных прямых секущей. Поэтому [[Image:20-06-61.jpg]]ADC= [[Image:20-06-61.jpg]]BCD. Утверждение доказано.<br>&nbsp;
 <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
-<sub>Видео по математике[[Математика|скачать]], домашнее задание, учителям и школьникам на помощь [[Гипермаркет знаний - первый в мире!|онлайн]]</sub>
+<sub>Видео по математике [[Математика|скачать]], домашнее задание, учителям и школьникам на помощь [[Гипермаркет знаний - первый в мире!|онлайн]]</sub>
 <br>

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: