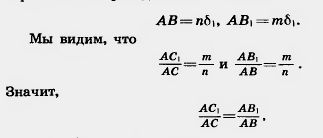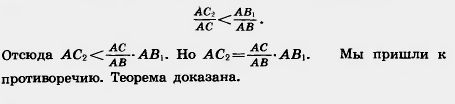|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | '''ТЕОРЕМА О ПРОПОРЦИОНАЛЬНЫХ ОТРЕЗКАХ'''<br> | + | '''ТЕОРЕМА О ПРОПОРЦИОНАЛЬНЫХ ОТРЕЗКАХ'''<br> |
| | | | |
| - | <br>Теорема 6.9. '''''Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.''''' | + | <br>Теорема 6.9. '''''Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.''''' |
| | | | |
| - | Доказательство. Пусть стороны угла А пересекаются параллельными прямыми в точках В, С и B<sub>1</sub>,С<sub>1</sub> соответственно (рис. 138). Теоремой утверждается, что<br> | + | Доказательство. Пусть стороны угла А пересекаются параллельными прямыми в точках В, С и B<sub>1</sub>,С<sub>1</sub> соответственно (рис. 138). Теоремой утверждается, что<br> |
| | | | |
| | [[Image:22-06-19.jpg]]<br><br>Докажем сначала равенство (*) в случае, когда существует такой отрезок длины [[Image:22-06-20.jpg]], который укладывается целое число раз и на отрезке АС, и на отрезке AС<sub>1</sub>. Пусть АС=n[[Image:22-06-20.jpg]], АС<sub>1</sub> = m[[Image:22-06-20.jpg]] и n>m. Разобьем отрезок АС на n равных частей (длины [[Image:22-06-20.jpg]]). При ЭТОМ точка С<sub>1</sub> будет одной из точек деления. | | [[Image:22-06-19.jpg]]<br><br>Докажем сначала равенство (*) в случае, когда существует такой отрезок длины [[Image:22-06-20.jpg]], который укладывается целое число раз и на отрезке АС, и на отрезке AС<sub>1</sub>. Пусть АС=n[[Image:22-06-20.jpg]], АС<sub>1</sub> = m[[Image:22-06-20.jpg]] и n>m. Разобьем отрезок АС на n равных частей (длины [[Image:22-06-20.jpg]]). При ЭТОМ точка С<sub>1</sub> будет одной из точек деления. |
| | | | |
| - | Проведем через точки деления прямые, параллельные прямой ВС. По теореме Фалеса эти прямые разбивают отрезок АВ на равные отрезки некоторой <br> | + | Проведем через точки деления прямые, параллельные прямой ВС. По теореме Фалеса эти прямые разбивают отрезок АВ на равные отрезки некоторой <br> |
| | | | |
| - | длины [[Image:22-06-20.jpg]]<sub>1</sub>). Имеем:<br> | + | длины [[Image:22-06-20.jpg]]<sub>1</sub>). Имеем:<br> |
| | | | |
| - | [[Image:22-06-21.jpg]]<br><br>что и требовалось доказать.<br>Докажем теорему в общем случае (не для запоминания). Допустим, что | + | [[Image:22-06-21.jpg]]<br><br>что и требовалось доказать.<br>Докажем теорему в общем случае (не для запоминания). Допустим, что |
| | | | |
| | [[Image:22-06-22.jpg]]<br><br>[[Image:22-06-23.jpg]]<br> | | [[Image:22-06-22.jpg]]<br><br>[[Image:22-06-23.jpg]]<br> |
| Строка 27: |
Строка 27: |
| | [[Image:22-06-25.jpg]]<br><br>Заменим в этом равенстве величину AY меньшей величиной AС<sub>2</sub>, а величину АХ большей величиной АВ<sub>1</sub>. Получим: | | [[Image:22-06-25.jpg]]<br><br>Заменим в этом равенстве величину AY меньшей величиной AС<sub>2</sub>, а величину АХ большей величиной АВ<sub>1</sub>. Получим: |
| | | | |
| | + | <br> |
| | | | |
| | + | [[Image:22-06-26.jpg]] |
| | | | |
| - | [[Image:22-06-26.jpg]]
| + | <br> |
| - | | + | |
| - | <br> | + | |
| | | | |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
Версия 07:21, 22 июня 2010
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Теорема о пропорциональных отрезках
ТЕОРЕМА О ПРОПОРЦИОНАЛЬНЫХ ОТРЕЗКАХ
Теорема 6.9. Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
Доказательство. Пусть стороны угла А пересекаются параллельными прямыми в точках В, С и B1,С1 соответственно (рис. 138). Теоремой утверждается, что

Докажем сначала равенство (*) в случае, когда существует такой отрезок длины 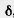 , который укладывается целое число раз и на отрезке АС, и на отрезке AС1. Пусть АС=n , который укладывается целое число раз и на отрезке АС, и на отрезке AС1. Пусть АС=n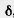 , АС1 = m , АС1 = m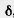 и n>m. Разобьем отрезок АС на n равных частей (длины и n>m. Разобьем отрезок АС на n равных частей (длины 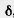 ). При ЭТОМ точка С1 будет одной из точек деления. ). При ЭТОМ точка С1 будет одной из точек деления.
Проведем через точки деления прямые, параллельные прямой ВС. По теореме Фалеса эти прямые разбивают отрезок АВ на равные отрезки некоторой
длины 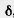 1). Имеем: 1). Имеем:
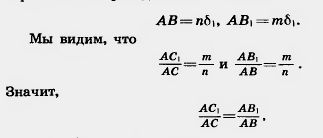
что и требовалось доказать.
Докажем теорему в общем случае (не для запоминания). Допустим, что
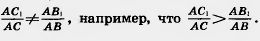
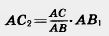
Отложим на луче АС отрезок Файл:22-06-24.jpg
При этом АС2<АС1. Разобьем отрезок АС на большое число n равных частей и проведем через точки деления прямые, параллельные ВС.
При достаточно большом n на отрезке С1С2 будут точки деления. Обозначим одну из них через У, а соответствующую точку на отрезке АВ1, через X. По доказанному
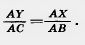
Заменим в этом равенстве величину AY меньшей величиной AС2, а величину АХ большей величиной АВ1. Получим:
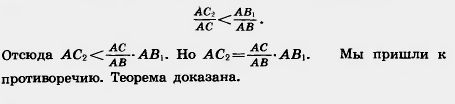
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Сборник конспектов уроков по математике скачать, календарно-тематическое планирование, учебники по всем предметам онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|