|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' ЗАДАЧИ'''<br><br>1. На рисунках 114—116 представлены три фигуры, каждая из которых состоит из четырех точек и четырех последовательно соединяющих их отрезков. Какая из этих фигур является четырехугольником? | + | ''' ЗАДАЧИ'''<br><br>1. На рисунках 114—116 представлены три фигуры, каждая из которых состоит из четырех точек и четырех последовательно соединяющих их отрезков. Какая из этих фигур является четырехугольником? |
| | | | |
| - | 2. Постройте какой-нибудь четырехугольник PQRS. Укажите его противолежащие стороны и вершины. | + | 2. Постройте какой-нибудь четырехугольник PQRS. Укажите его противолежащие стороны и вершины. |
| | | | |
| - | 3. Сколько можно построить параллелограммов с вершинами в трех заданных точках, не лежащих на одной прямой? Постройте их. | + | 3. Сколько можно построить параллелограммов с вершинами в трех заданных точках, не лежащих на одной прямой? Постройте их. |
| | | | |
| | 4. Боковая сторона равнобедренного треугольника равна 5 м. Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма. | | 4. Боковая сторона равнобедренного треугольника равна 5 м. Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма. |
| | | | |
| - | 5. Расстояния от точки пересечения диагоналей парал-лелограмма до двух его вершин равны 3 см и 4 см. Чему равны расстояния от нее до двух других вершин? Объясните ответ. | + | 5. Расстояния от точки пересечения диагоналей парал-лелограмма до двух его вершин равны 3 см и 4 см. Чему равны расстояния от нее до двух других вершин? Объясните ответ. |
| | | | |
| - | 6. Через точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что отрезок ее, заключенный между параллельными сторонами, делится этой точкой пополам. | + | 6. Через точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что отрезок ее, заключенный между параллельными сторонами, делится этой точкой пополам. |
| | | | |
| - | 7. В параллелограмме ABCD через точку пересечения диагоналей проведена прямая, которая отсекает на сторонах ВС и AD отрезки BE = 2 м и AF = 2,8 м. Найдите стороны ВС и AD. | + | 7. В параллелограмме ABCD через точку пересечения диагоналей проведена прямая, которая отсекает на сторонах ВС и AD отрезки BE = 2 м и AF = 2,8 м. Найдите стороны ВС и AD. |
| | | | |
| - | 8. У параллелограмма ABCD АВ=10 см, ВС = 15 см. Чему равны стороны AD и CD? Объясните ответ. | + | 8. У параллелограмма ABCD АВ=10 см, ВС = 15 см. Чему равны стороны AD и CD? Объясните ответ. |
| | | | |
| - | 9. У параллелограмма ABCD АА = ЪО°. Чему равны углы В, С, D? Объясните ответ. | + | 9. У параллелограмма ABCD АА = ЪО°. Чему равны углы В, С, D? Объясните ответ. |
| | | | |
| - | 10. Периметр параллелограмма ABCD равен 10 см. Найдите длину диагонали BD, зная, что периметр треугольника ABD равен 8 см. | + | 10. Периметр параллелограмма ABCD равен 10 см. Найдите длину диагонали BD, зная, что периметр треугольника ABD равен 8 см. |
| | | | |
| - | 11. Один из углов параллелограмма равен 40°. Найдите остальные углы. | + | 11. Один из углов параллелограмма равен 40°. Найдите остальные углы. |
| | | | |
| - | 12. Найдите углы параллелограмма, зная, что один из них больше другого на 50°. | + | 12. Найдите углы параллелограмма, зная, что один из них больше другого на 50°. |
| | | | |
| - | 13. Может ли один угол параллелограмма быть равным 40°, а другой — 50°? | + | 13. Может ли один угол параллелограмма быть равным 40°, а другой — 50°? |
| | | | |
| - | 14. Диагональ параллелограмма образует с двумя его сторонами углы 25" и 35^. Найдите углы параллелограмма. | + | 14. Диагональ параллелограмма образует с двумя его сторонами углы 25" и 35^. Найдите углы параллелограмма. |
| | | | |
| - | 15. Найдите все углы параллелограмма, если сумма двух из них равна: 1) 80"; 2) 100°; 3) 160°. | + | 15. Найдите все углы параллелограмма, если сумма двух из них равна: 1) 80"; 2) 100°; 3) 160°. |
| | | | |
| - | 16. Найдите все углы параллелограмма, если разность двух из них равна:1) 70°; 2) 110°; 3) 140°. | + | 16. Найдите все углы параллелограмма, если разность двух из них равна:1) 70°; 2) 110°; 3) 140°. |
| | | | |
| - | 17. В параллелограмме ABCD точка Е — середина стороны ВС, а F — середина стороны AD. Докажите, что четырехугольник BEDF — параллелограмм. | + | 17. В параллелограмме ABCD точка Е — середина стороны ВС, а F — середина стороны AD. Докажите, что четырехугольник BEDF — параллелограмм. |
| | | | |
| - | 18. Докажите, что если у четырехугольника две стороны параллельны и равны, то он является параллелограммом. | + | 18. Докажите, что если у четырехугольника две стороны параллельны и равны, то он является параллелограммом. |
| | | | |
| - | 19. В параллелограмме ABCD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е. Чему равны отрезки BE и ЕС, если АВ = 9 см, AD= 15 см? | + | 19. В параллелограмме ABCD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е. Чему равны отрезки BE и ЕС, если АВ = 9 см, AD= 15 см? |
| | | | |
| - | 20. Две стороны параллелограмма относятся как 3:4, а периметр его равен 2,8 м. Найдите стороны. | + | 20. Две стороны параллелограмма относятся как 3:4, а периметр его равен 2,8 м. Найдите стороны. |
| | | | |
| | + | <br> |
| | | | |
| | + | [[Image:22-06-32.jpg]]<br><br>21. В параллелограмме ABCD перпендикуляр, опущенный из вершины В на сторону AD, делит ее пополам. Найдите диагональ BD и стороны параллелограмма, если известно, что периметр параллелограмма равен 3,8 м, а периметр треугольника ABD равен 3 м. |
| | | | |
| - | [[Image:22-06-32.jpg]]<br><br>21. В параллелограмме ABCD перпендикуляр, опущенный из вершины В на сторону AD, делит ее пополам. Найдите диагональ BD и стороны параллелограмма, если известно, что периметр параллелограмма равен 3,8 м, а периметр треугольника ABD равен 3 м.
| + | 22. Постройте параллелограмм: |
| | | | |
| - | 22. Постройте параллелограмм:
| + | 1) по двум сторонам и диагонали; |
| | | | |
| - | 1) по двум сторонам и диагонали;
| + | 2) по стороне и двум диагоналям. |
| | | | |
| - | 2) по стороне и двум диагоналям.
| + | 23. Постройте параллелограмм: |
| - | | + | |
| - | 23. Постройте параллелограмм: | + | |
| | | | |
| | 1) по двум сторонам и углу; | | 1) по двум сторонам и углу; |
| | | | |
| - | 2) по диагоналям и углу между ними. | + | 2) по диагоналям и углу между ними. |
| | | | |
| - | 24. Докажите, что если у параллелограмма все углы равны, то он является прямоугольником. | + | 24. Докажите, что если у параллелограмма все углы равны, то он является прямоугольником. |
| | | | |
| - | 25. Докажите, что если в параллелограмме хотя бы один угол прямой, то он является прямоугольником. | + | 25. Докажите, что если в параллелограмме хотя бы один угол прямой, то он является прямоугольником. |
| | | | |
| - | 26. Докажите, что если у параллелограмма диагонали равны, то он является прямоугольником. | + | 26. Докажите, что если у параллелограмма диагонали равны, то он является прямоугольником. |
| | | | |
| - | 27. Бетонная плита с прямолинейными краями должна иметь форму прямоугольника. Как при помощи бечевки проверить правильность формы плиты? | + | 27. Бетонная плита с прямолинейными краями должна иметь форму прямоугольника. Как при помощи бечевки проверить правильность формы плиты? |
| | | | |
| - | 28. Биссектриса одного из углов прямоугольника делит сторону прямоугольника пополам. Найдите периметр прямоугольника, если его меньшая сторона равна 10 см. | + | 28. Биссектриса одного из углов прямоугольника делит сторону прямоугольника пополам. Найдите периметр прямоугольника, если его меньшая сторона равна 10 см. |
| | | | |
| - | 29. В прямоугольнике точка пересечения диагоналей отстоит от меньшей стороны на 4 см дальше, чем от большей стороны. Периметр прямоугольника равен 56 см. Найдите стороны прямоугольника. | + | 29. В прямоугольнике точка пересечения диагоналей отстоит от меньшей стороны на 4 см дальше, чем от большей стороны. Периметр прямоугольника равен 56 см. Найдите стороны прямоугольника. |
| | | | |
| - | 30. Из одной точки окружности проведены две взаимно перпендикулярные хорды, которые удалены от центра на 6 см и 10 см. Найдите их длины. | + | 30. Из одной точки окружности проведены две взаимно перпендикулярные хорды, которые удалены от центра на 6 см и 10 см. Найдите их длины. |
| | | | |
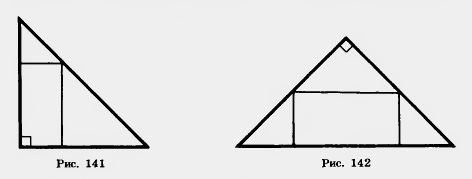
| - | 31. В прямоугольный треугольник, каждый катет которого равен 6 см, вписан прямоугольник, имеющий с треугольником общий угол (рис. 141). Найдите периметр прямоугольника. | + | 31. В прямоугольный треугольник, каждый катет которого равен 6 см, вписан прямоугольник, имеющий с треугольником общий угол (рис. 141). Найдите периметр прямоугольника. |
| | | | |
| | 32. В равнобедренный прямоугольный треугольник вписан прямоугольник так, что две его вершины находятся на гипотенузе, а две другие — на катетах (рис. 142). Чему равны стороны прямоугольника, если известно, что они относятся как 5:2, а гипотенуза треугольника равна 45 см? | | 32. В равнобедренный прямоугольный треугольник вписан прямоугольник так, что две его вершины находятся на гипотенузе, а две другие — на катетах (рис. 142). Чему равны стороны прямоугольника, если известно, что они относятся как 5:2, а гипотенуза треугольника равна 45 см? |
| | | | |
| - | 33. Докажите, что если у параллелограмма диагонали перпендикулярны, то он является ромбом. | + | 33. Докажите, что если у параллелограмма диагонали перпендикулярны, то он является ромбом. |
| | | | |
| - | 34.Докажите, что если диагональ параллелограмма является биссектрисой его углов, то он является ромбом. | + | 34.Докажите, что если диагональ параллелограмма является биссектрисой его углов, то он является ромбом. |
| | | | |
| - | 35.Углы, образуемые диагоналями ромба с одной из его сторон, относятся как 4:5. Найдите углы ромба. | + | 35.Углы, образуемые диагоналями ромба с одной из его сторон, относятся как 4:5. Найдите углы ромба. |
| | | | |
| - | 36.Докажите, что четырехугольник, у которого все стороны равны, является ромбом. | + | 36.Докажите, что четырехугольник, у которого все стороны равны, является ромбом. |
| | | | |
| - | 37.В ромбе одна из диагоналей равна стороне. Найдите углы ромба. | + | 37.В ромбе одна из диагоналей равна стороне. Найдите углы ромба. |
| | | | |
| - | 38.Постройте ромб: | + | 38.Постройте ромб: |
| | | | |
| - | 1) по углу и диагонали, исходящей из вершины этого угла; | + | 1) по углу и диагонали, исходящей из вершины этого угла; |
| | | | |
| - | 2) по диагонали и противолежащему углу. | + | 2) по диагонали и противолежащему углу. |
| | | | |
| - | 39.Постройте ромб: | + | 39.Постройте ромб: |
| | | | |
| | 1) по стороне и диагонали; | | 1) по стороне и диагонали; |
| | | | |
| - | 2) по двум диагоналям. | + | 2) по двум диагоналям. |
| | | | |
| - | 40. Докажите, что если диагонали прямоугольника пересекаются под прямым углом, то он есть квадрат. | + | 40. Докажите, что если диагонали прямоугольника пересекаются под прямым углом, то он есть квадрат. |
| | | | |
| - | 41.В равнобедренный прямоугольный треугольник, каждый катет которого 2 м, вписан квадрат, имеющий с ним общий угол. Найдите периметр квадрата. | + | 41.В равнобедренный прямоугольный треугольник, каждый катет которого 2 м, вписан квадрат, имеющий с ним общий угол. Найдите периметр квадрата. |
| | | | |
| | 42.Дан квадрат ABCD. На каждой из его сторон отложены равные отрезки: AA<sub>1</sub>=BB<sub>1</sub>=CC<sub>1</sub>=DD<sub>1</sub>. Докажите, что четырехугольник A<sub>1</sub>B<sub>1</sub>C<sub>1</sub>D<sub>1</sub> есть квадрат (рис. | | 42.Дан квадрат ABCD. На каждой из его сторон отложены равные отрезки: AA<sub>1</sub>=BB<sub>1</sub>=CC<sub>1</sub>=DD<sub>1</sub>. Докажите, что четырехугольник A<sub>1</sub>B<sub>1</sub>C<sub>1</sub>D<sub>1</sub> есть квадрат (рис. |
| | | | |
| - | 143). | + | 143). |
| | | | |
| - | 43.Диагональ квадрата равна 4 м. Сторона его равна диагонали другого квадрата. Найдите сторону последнего. | + | 43.Диагональ квадрата равна 4 м. Сторона его равна диагонали другого квадрата. Найдите сторону последнего. |
| | | | |
| - | 44.Дан квадрат, сторона которого 1 м, диагональ его равна стороне другого квадрата. Найдите диагональ последнего. | + | 44.Дан квадрат, сторона которого 1 м, диагональ его равна стороне другого квадрата. Найдите диагональ последнего. |
| | | | |
| - | 45.В квадрат (рис. 144) вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина<br> <br>[[Image:22-06-33.jpg]]<br> <br>прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Найдите стороны прямоугольника, зная, что одна из них вдвое больше другой и что диагональ квадрата равна 12 м. | + | 45.В квадрат (рис. 144) вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина<br> <br>[[Image:22-06-33.jpg]]<br> <br>прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Найдите стороны прямоугольника, зная, что одна из них вдвое больше другой и что диагональ квадрата равна 12 м. |
| | | | |
| - | 46. В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины находятся на гипотенузе, а другие две — на катетах. Найдите сторону квадрата, если известно, что гипотенуза равна 3 м. | + | 46. В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины находятся на гипотенузе, а другие две — на катетах. Найдите сторону квадрата, если известно, что гипотенуза равна 3 м. |
| | | | |
| - | 47. Из данной точки проведены к окружности две взаимно перпендикулярные касательные, радиус окружности 10 см. Найдите длины касательных (расстояние от данной точки до точки касания). | + | 47. Из данной точки проведены к окружности две взаимно перпендикулярные касательные, радиус окружности 10 см. Найдите длины касательных (расстояние от данной точки до точки касания). |
| | | | |
| - | 48. Разделите данный отрезок АВ на п равных частей. | + | 48. Разделите данный отрезок АВ на п равных частей. |
| | | | |
| | 49. Разделите данный отрезок на указанное число равных частей: 1) 3; 2) 5; 3) 6. | | 49. Разделите данный отрезок на указанное число равных частей: 1) 3; 2) 5; 3) 6. |
| | | | |
| - | 50. Стороны треугольника равны 8 см, 10 см, 12 см. Найдите стороны треугольника, вершинами которого являются середины сторон данного треугольника. | + | 50. Стороны треугольника равны 8 см, 10 см, 12 см. Найдите стороны треугольника, вершинами которого являются середины сторон данного треугольника. |
| | + | |
| | + | 51. Периметр треугольника равен 12 см, середины сторон соединены отрезками. Найдите периметр полученного треугольника. |
| | + | |
| | + | 52. Средняя линия равнобедренного треугольника, параллельная основанию, равна 3 см. Найдите стороны треугольника, если его периметр равен 16 см. |
| | + | |
| | + | 53. Как построить треугольник, если заданы середины его сторон? |
| | + | |
| | + | 54. Докажите, что вершины треугольника равноудалены от прямой, проходящей через середины двух его сторон. |
| | + | |
| | + | 55. Докажите, что середины сторон четырехугольника являются вершинами параллелограмма. |
| | + | |
| | + | 56. Найдите стороны параллелограмма из предыдущей задачи, если известно, что диагонали четырехугольника равны 10 м и 12 м. |
| | + | |
| | + | 57. У четырехугольника диагонали равны а и Ь. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника. |
| | + | |
| | + | 58. Докажите, что середины сторон прямоугольника являются вершинами ромба. И наоборот, середины сторон ромба являются вершинами прямоугольника. |
| | + | |
| | + | 59. Боковая сторона трапеции разделена на три равные части, и из точек деления проведены к другой стороне отрезки, параллельные основаниям. Найдите длины этих отрезков, если основания трапеции равны 2 м и 5 м. |
| | + | |
| | + | 60. Докажите, что у равнобокой трапеции углы при основании равны. |
| | + | |
| | + | 61. Чему равны углы равнобокой трапеции, если известно, что разность противолежащих углов равна 40°? |
| | + | |
| | + | 62. В равнобокой трапеции большее основание равно 2,7 м, боковая сторона равна 1 м, угол между ними 60°. Найдите меньшее основание. |
| | + | |
| | + | 63. В равнобокой трапеции высота, проведенная из вершины тупого угла, делит большее основание на отрезки 6 см и 30 см. Найдите основания трапеции. |
| | + | |
| | + | 64*. Меньшее основание равнобокой трапеции равно боковой стороне, а диагональ перпендикулярна боковой стороне (рис. 145). Найдите углы трапеции. |
| | + | |
| | + | 65. По одну сторону от прямой а даны две точки А и В на расстояниях 10 м и 20 м от нее. Найдите расстояние от середины отрезка АВ до прямой а. |
| | + | |
| | + | 66. По разные стороны от прямой а даны две точки А н В на расстояниях 10 см и 4 см от нее. Найдите расстояние от середины отрезка АВ до прямой а. |
| | + | |
| | + | 67. Основания трапеции относятся как 2:3, а средняя линия равна 5 м. Найдите основания. |
| | + | |
| | + | 68. Концы диаметра удалены от касательной к окружности на 1,6 ми 0,6 м. Найдите длину диаметра. |
| | + | |
| | + | 69. Средняя линия трапеции 7 см, а одно из ее оснований больше другого на 4 см. Найдите основания трапеции. |
| | + | |
| | + | 70. Высота, проведенная из вершины тупого угла равнобокой трапеции, делит большее основание на части, имеющие длины а и b (а> b). Найдите среднюю линию трапеции. |
| | + | |
| | + | 71*. Постройте трапецию по основаниям и боковым сторонам. |
| | + | |
| | + | 72*. Постройте трапецию по основаниям и диагоналям. |
| | | | |
| - | 51. Периметр треугольника равен 12 см, середины сторон соединены отрезками. Найдите периметр полученного треугольника.
| + | 73*. Даны отрезки а, Ь, с, d, е. Постройте отрезок [[Image:22-06-34.jpg]]. |
| | | | |
| - | 52. Средняя линия равнобедренного треугольника, параллельная основанию, равна 3 см. Найдите стороны треугольника, если его периметр равен 16 см.<br>53. Как построить треугольник, если заданы середины его сторон?<br>54. Докажите, что вершины треугольника равноудалены от прямой, проходящей через середины двух его сторон.<br>55. Докажите, что середины сторон четырехугольника являются вершинами параллелограмма.<br>56. Найдите стороны параллелограмма из предыдущей задачи, если известно, что диагонали четырехугольника равны 10 м и 12 м.<br>57. У четырехугольника диагонали равны а и Ь. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.<br>58. Докажите, что середины сторон прямоугольника являются вершинами ромба. И наоборот, середины сторон ромба являются вершинами прямоугольника.<br>59<br>59. Боковая сторона трапеции разделена на три равные части, и из точек деления проведены к другой стороне отрезки, параллельные основаниям. Найдите длины этих отрезков, если основания трапеции равны 2 м и 5 м.<br>60. Докажите, что у равнобокой трапеции углы при основании равны.<br> <br>61. Чему равны углы равнобокой трапеции, если известно, что разность противолежащих углов равна 40°?<br>62. В равнобокой трапеции большее основание равно 2,7 м, боковая сторона равна 1 м, угол между ними 60°. Найдите меньшее основание.<br>63. В равнобокой трапеции высота, проведенная из вершины тупого угла, делит большее основание на отрезки 6 см и 30 см. Найдите основания трапеции.<br>64*. Меньшее основание равнобокой трапеции равно боковой стороне, а диагональ перпендикулярна боковой стороне (рис. 145). Найдите углы трапеции.<br>65. По одну сторону от прямой а даны две точки А и В на расстояниях 10 м и 20 м от нее. Найдите расстояние от середины отрезка АВ до прямой а.<br>66. По разные стороны от прямой а даны две точки А н В на расстояниях 10 см и 4 см от нее. Найдите расстояние от середины отрезка АВ до прямой а.<br>67. Основания трапеции относятся как 2:3, а средняя линия равна 5 м. Найдите основания.<br>68. Концы диаметра удалены от касательной к окружности на 1,6 ми 0,6 м. Найдите длину диаметра.<br>69. Средняя линия трапеции 7 см, а одно из ее оснований больше другого на 4 см. Найдите основания трапеции.<br>70. Высота, проведенная из вершины тупого угла равнобокой трапеции, делит большее основание на части, имеющие длины а н Ъ {а> Ъ). Найдите среднюю линию трапеции.<br>71*. Постройте трапецию по основаниям и боковым сторонам. 72*. Постройте трапецию по основаниям и диагоналям.<br>73*. Даны отрезки а, Ь, с, d, е. Постройте отрезок л:=^.<br>61<br>74*. 1) В треугольнике ABC проведены медианы АА\ и ВВ\, которые пересекаются в точке М (рис. 146). В треугольнике<br> <br><br> <br><br> <br>АМВ проведена средняя линия PQ. Докажите, что четырехугольник A\B\PQ — параллелограмм.<br>2) Докажите, что любые две медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины.<br>3) Докажите, что все три медианы треугольника пересекаются в одной точке.<br><br><br>
| + | 74*. 1) В треугольнике ABC проведены медианы АА\ и ВВ\, которые пересекаются в точке М (рис. 146). В треугольнике<br> <br>[[Image:22-06-35.jpg]]<br> <br>АМВ проведена средняя линия PQ. Докажите, что четырехугольник A<sub>1</sub>B<sub>1</sub>PQ — параллелограмм.<br>2) Докажите, что любые две медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины.<br>3) Докажите, что все три медианы треугольника пересекаются в одной точке.<br><br><br> |
| | | | |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
Версия 08:03, 22 июня 2010
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Задачи-1(8 класс)
ЗАДАЧИ
1. На рисунках 114—116 представлены три фигуры, каждая из которых состоит из четырех точек и четырех последовательно соединяющих их отрезков. Какая из этих фигур является четырехугольником?
2. Постройте какой-нибудь четырехугольник PQRS. Укажите его противолежащие стороны и вершины.
3. Сколько можно построить параллелограммов с вершинами в трех заданных точках, не лежащих на одной прямой? Постройте их.
4. Боковая сторона равнобедренного треугольника равна 5 м. Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма.
5. Расстояния от точки пересечения диагоналей парал-лелограмма до двух его вершин равны 3 см и 4 см. Чему равны расстояния от нее до двух других вершин? Объясните ответ.
6. Через точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что отрезок ее, заключенный между параллельными сторонами, делится этой точкой пополам.
7. В параллелограмме ABCD через точку пересечения диагоналей проведена прямая, которая отсекает на сторонах ВС и AD отрезки BE = 2 м и AF = 2,8 м. Найдите стороны ВС и AD.
8. У параллелограмма ABCD АВ=10 см, ВС = 15 см. Чему равны стороны AD и CD? Объясните ответ.
9. У параллелограмма ABCD АА = ЪО°. Чему равны углы В, С, D? Объясните ответ.
10. Периметр параллелограмма ABCD равен 10 см. Найдите длину диагонали BD, зная, что периметр треугольника ABD равен 8 см.
11. Один из углов параллелограмма равен 40°. Найдите остальные углы.
12. Найдите углы параллелограмма, зная, что один из них больше другого на 50°.
13. Может ли один угол параллелограмма быть равным 40°, а другой — 50°?
14. Диагональ параллелограмма образует с двумя его сторонами углы 25" и 35^. Найдите углы параллелограмма.
15. Найдите все углы параллелограмма, если сумма двух из них равна: 1) 80"; 2) 100°; 3) 160°.
16. Найдите все углы параллелограмма, если разность двух из них равна:1) 70°; 2) 110°; 3) 140°.
17. В параллелограмме ABCD точка Е — середина стороны ВС, а F — середина стороны AD. Докажите, что четырехугольник BEDF — параллелограмм.
18. Докажите, что если у четырехугольника две стороны параллельны и равны, то он является параллелограммом.
19. В параллелограмме ABCD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е. Чему равны отрезки BE и ЕС, если АВ = 9 см, AD= 15 см?
20. Две стороны параллелограмма относятся как 3:4, а периметр его равен 2,8 м. Найдите стороны.
21. В параллелограмме ABCD перпендикуляр, опущенный из вершины В на сторону AD, делит ее пополам. Найдите диагональ BD и стороны параллелограмма, если известно, что периметр параллелограмма равен 3,8 м, а периметр треугольника ABD равен 3 м.
22. Постройте параллелограмм:
1) по двум сторонам и диагонали;
2) по стороне и двум диагоналям.
23. Постройте параллелограмм:
1) по двум сторонам и углу;
2) по диагоналям и углу между ними.
24. Докажите, что если у параллелограмма все углы равны, то он является прямоугольником.
25. Докажите, что если в параллелограмме хотя бы один угол прямой, то он является прямоугольником.
26. Докажите, что если у параллелограмма диагонали равны, то он является прямоугольником.
27. Бетонная плита с прямолинейными краями должна иметь форму прямоугольника. Как при помощи бечевки проверить правильность формы плиты?
28. Биссектриса одного из углов прямоугольника делит сторону прямоугольника пополам. Найдите периметр прямоугольника, если его меньшая сторона равна 10 см.
29. В прямоугольнике точка пересечения диагоналей отстоит от меньшей стороны на 4 см дальше, чем от большей стороны. Периметр прямоугольника равен 56 см. Найдите стороны прямоугольника.
30. Из одной точки окружности проведены две взаимно перпендикулярные хорды, которые удалены от центра на 6 см и 10 см. Найдите их длины.
31. В прямоугольный треугольник, каждый катет которого равен 6 см, вписан прямоугольник, имеющий с треугольником общий угол (рис. 141). Найдите периметр прямоугольника.
32. В равнобедренный прямоугольный треугольник вписан прямоугольник так, что две его вершины находятся на гипотенузе, а две другие — на катетах (рис. 142). Чему равны стороны прямоугольника, если известно, что они относятся как 5:2, а гипотенуза треугольника равна 45 см?
33. Докажите, что если у параллелограмма диагонали перпендикулярны, то он является ромбом.
34.Докажите, что если диагональ параллелограмма является биссектрисой его углов, то он является ромбом.
35.Углы, образуемые диагоналями ромба с одной из его сторон, относятся как 4:5. Найдите углы ромба.
36.Докажите, что четырехугольник, у которого все стороны равны, является ромбом.
37.В ромбе одна из диагоналей равна стороне. Найдите углы ромба.
38.Постройте ромб:
1) по углу и диагонали, исходящей из вершины этого угла;
2) по диагонали и противолежащему углу.
39.Постройте ромб:
1) по стороне и диагонали;
2) по двум диагоналям.
40. Докажите, что если диагонали прямоугольника пересекаются под прямым углом, то он есть квадрат.
41.В равнобедренный прямоугольный треугольник, каждый катет которого 2 м, вписан квадрат, имеющий с ним общий угол. Найдите периметр квадрата.
42.Дан квадрат ABCD. На каждой из его сторон отложены равные отрезки: AA1=BB1=CC1=DD1. Докажите, что четырехугольник A1B1C1D1 есть квадрат (рис.
143).
43.Диагональ квадрата равна 4 м. Сторона его равна диагонали другого квадрата. Найдите сторону последнего.
44.Дан квадрат, сторона которого 1 м, диагональ его равна стороне другого квадрата. Найдите диагональ последнего.
45.В квадрат (рис. 144) вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина
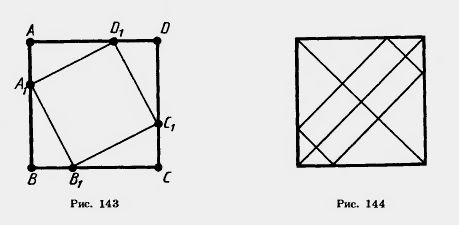
прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Найдите стороны прямоугольника, зная, что одна из них вдвое больше другой и что диагональ квадрата равна 12 м.
46. В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины находятся на гипотенузе, а другие две — на катетах. Найдите сторону квадрата, если известно, что гипотенуза равна 3 м.
47. Из данной точки проведены к окружности две взаимно перпендикулярные касательные, радиус окружности 10 см. Найдите длины касательных (расстояние от данной точки до точки касания).
48. Разделите данный отрезок АВ на п равных частей.
49. Разделите данный отрезок на указанное число равных частей: 1) 3; 2) 5; 3) 6.
50. Стороны треугольника равны 8 см, 10 см, 12 см. Найдите стороны треугольника, вершинами которого являются середины сторон данного треугольника.
51. Периметр треугольника равен 12 см, середины сторон соединены отрезками. Найдите периметр полученного треугольника.
52. Средняя линия равнобедренного треугольника, параллельная основанию, равна 3 см. Найдите стороны треугольника, если его периметр равен 16 см.
53. Как построить треугольник, если заданы середины его сторон?
54. Докажите, что вершины треугольника равноудалены от прямой, проходящей через середины двух его сторон.
55. Докажите, что середины сторон четырехугольника являются вершинами параллелограмма.
56. Найдите стороны параллелограмма из предыдущей задачи, если известно, что диагонали четырехугольника равны 10 м и 12 м.
57. У четырехугольника диагонали равны а и Ь. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
58. Докажите, что середины сторон прямоугольника являются вершинами ромба. И наоборот, середины сторон ромба являются вершинами прямоугольника.
59. Боковая сторона трапеции разделена на три равные части, и из точек деления проведены к другой стороне отрезки, параллельные основаниям. Найдите длины этих отрезков, если основания трапеции равны 2 м и 5 м.
60. Докажите, что у равнобокой трапеции углы при основании равны.
61. Чему равны углы равнобокой трапеции, если известно, что разность противолежащих углов равна 40°?
62. В равнобокой трапеции большее основание равно 2,7 м, боковая сторона равна 1 м, угол между ними 60°. Найдите меньшее основание.
63. В равнобокой трапеции высота, проведенная из вершины тупого угла, делит большее основание на отрезки 6 см и 30 см. Найдите основания трапеции.
64*. Меньшее основание равнобокой трапеции равно боковой стороне, а диагональ перпендикулярна боковой стороне (рис. 145). Найдите углы трапеции.
65. По одну сторону от прямой а даны две точки А и В на расстояниях 10 м и 20 м от нее. Найдите расстояние от середины отрезка АВ до прямой а.
66. По разные стороны от прямой а даны две точки А н В на расстояниях 10 см и 4 см от нее. Найдите расстояние от середины отрезка АВ до прямой а.
67. Основания трапеции относятся как 2:3, а средняя линия равна 5 м. Найдите основания.
68. Концы диаметра удалены от касательной к окружности на 1,6 ми 0,6 м. Найдите длину диаметра.
69. Средняя линия трапеции 7 см, а одно из ее оснований больше другого на 4 см. Найдите основания трапеции.
70. Высота, проведенная из вершины тупого угла равнобокой трапеции, делит большее основание на части, имеющие длины а и b (а> b). Найдите среднюю линию трапеции.
71*. Постройте трапецию по основаниям и боковым сторонам.
72*. Постройте трапецию по основаниям и диагоналям.
73*. Даны отрезки а, Ь, с, d, е. Постройте отрезок 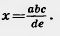 . .
74*. 1) В треугольнике ABC проведены медианы АА\ и ВВ\, которые пересекаются в точке М (рис. 146). В треугольнике
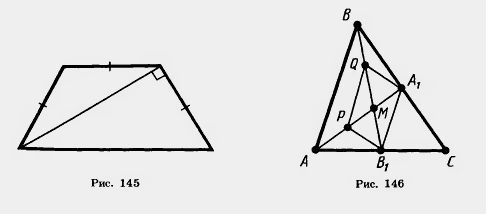
АМВ проведена средняя линия PQ. Докажите, что четырехугольник A1B1PQ — параллелограмм.
2) Докажите, что любые две медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины.
3) Докажите, что все три медианы треугольника пересекаются в одной точке.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Планы конспектов уроков по математике 8 класса скачать, учебники и книги бесплатно, разработки уроков по математике онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|













